单项式乘多项式[上学期]
图片预览


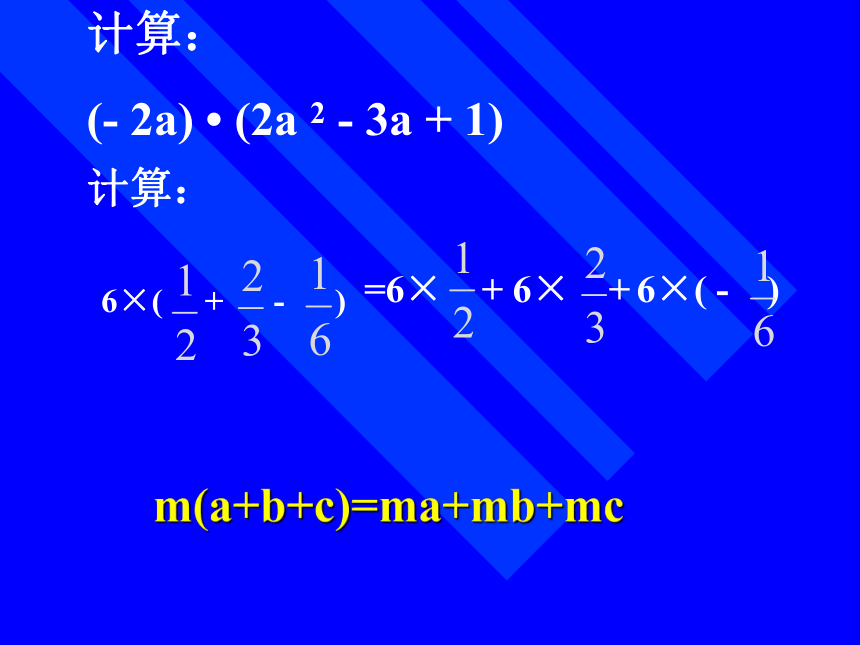





文档简介
课件20张PPT。复习提问:1. 请说出单项式与单项式相乘的法则: 单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。2. 什么叫多项式? 几个单项式的和叫做多项式。在多项式中,每个单项式叫做多项式的项。3. 什么叫多项式的项?·(x 2 y2)单项式与多项式相乘计算:
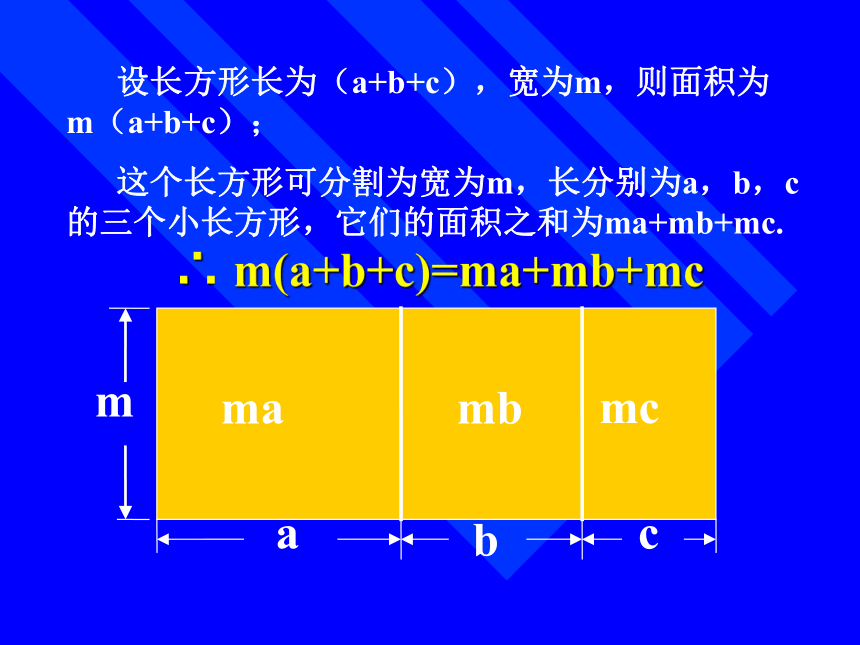
(- 2a) ? (2a 2 - 3a + 1) m(a+b+c)=ma+mb+mc 设长方形长为(a+b+c),宽为m,则面积为m(a+b+c); 这个长方形可分割为宽为m,长分别为a,b,c的三个小长方形,它们的面积之和为ma+mb+mc. ∴ m(a+b+c)=ma+mb+mc计算:
(- 2a) ? (2a 2 - 3a + 1)= (- 2a) ? 2a 2 +(- 2a) ?( - 3a)+(- 2a) ? 1= - 4a3+6a2 - 2a(乘法分配律)(单项式乘法)单项式与多项式相乘法则 单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加。例1 计算:
(1) (- 4x) (2x2+3x-1)解:原式=(- 4x) ?2x2+(- 4x)?3x+(- 4x)?(-1) = - 8x3- 12x2+4x单项式与多项式相乘时,分两个阶段:①按乘法分配律把乘积写成单项式与单项式乘积的代数和的形式;②单项式的乘法运算。几点注意:1.单项式乘多项式的结果仍是多项式,积的
项数与原多项式的项数相同。2.在单项式乘法运算中要注意系数的符号。 3.不要出现漏乘现象,运算要有顺序。解:原式= - a3b - 2a2b 2 - 5a3b+5a2b2= - 6a3b+3a2b2例3 计算:
( -2ab )3 ( 5a2b – 0.5ab2+0.25b3 )解:原式=(-8a 3 b 3) ( 5a2b – 0.5ab2+0.25b3 ) =(-8a 3 b 3) ·(5a2b) +(-8a 3 b 3) ·(- 0.5ab2 )
+(-8a 3 b 3) ·(0.25b3 ) = - 40a 5b4+4a4b 5– 2a3b6说明:先进行乘方运算,
再进行单项式与多项式的乘法运算。例4 计算:x [ x(x - 1)- 1]解法一: x [ x(x - 1)- 1] 解法二: x [ x(x - 1)- 1]= x [(x 2– x)- 1]= x (x 2– x – 1)说明:先去小括号,再去中括号。= x3 – x2 - x= x3 – x2 - x= x ? x(x - 1)- x= x2(x - 1)- x说明:先把x(x – 1)看成整体,按乘法对加法的分配律去掉中括号,再去掉小括号。几点注意:1.解题方法的灵活选择。2. 有同类项要合并。例5 解方程
7x -(x – 3)x – 3x(2 – x)=(2x + 1)x + 6解:去括号,得
7x – x 2+ 3x – 6x + 3x 2 = 2x 2 + x + 6移项,得
7x – x 2+ 3x – 6x + 3x 2 - 2x 2 - x = 6合并同类项,得 3x = 6系数化为1,得 x = 2 例6 求值:
yn(yn + 9y - 12) – 3(3yn+1 - 4yn),
其中y= - 3,n=2.解: yn(yn + 9y - 12) – 3(3yn+1 - 4yn)= y 2n+ 9yn+1- 12 yn– 9yn+1 +12 yn= y 2n当y= - 3,n=2时,原式=(- 3)4=81 求值问题,方法不是惟一
的,可以直接把字母的值代入
原式,但计算繁琐易出错,应
先化简,再代入求值,就显得
非常简捷。
例7 如图,计算图中阴影部分的面积.AB=7a,
BC=6bABCDEFGH 分析:阴影部分即长方形ABCD减去
以下四部分:梯形ADGF,△ GCF,△ AHE,
梯形HBCEABCDEFGHAB=7a,
BC=6b
解:阴影部分的面积为:小结: 单项式与多项式相乘的依据是:
乘法对加法的分配律。 单项式与多项式相乘,其积仍是多项式,项数与原多项式的项数 相同,注意不要漏乘项。 积的每一项的符号由原多项式各项符号和单项式的符号来决定,注意去括号法则。作业:实验版:
习题6.1.4 A组 1.(1,3,4,6),2.(2,3,5,6),
3.
B组 1. 2. 3.人教版:
习题7.4:A组 1.(2,5,7,8), 2.(2,3,5,6),
3.(2,4),4.
B组 1. 2.选作题:
设p = x – 1,
计算p ? (xn+xn-1+xn-2+…+x+1)
(- 2a) ? (2a 2 - 3a + 1) m(a+b+c)=ma+mb+mc 设长方形长为(a+b+c),宽为m,则面积为m(a+b+c); 这个长方形可分割为宽为m,长分别为a,b,c的三个小长方形,它们的面积之和为ma+mb+mc. ∴ m(a+b+c)=ma+mb+mc计算:
(- 2a) ? (2a 2 - 3a + 1)= (- 2a) ? 2a 2 +(- 2a) ?( - 3a)+(- 2a) ? 1= - 4a3+6a2 - 2a(乘法分配律)(单项式乘法)单项式与多项式相乘法则 单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加。例1 计算:
(1) (- 4x) (2x2+3x-1)解:原式=(- 4x) ?2x2+(- 4x)?3x+(- 4x)?(-1) = - 8x3- 12x2+4x单项式与多项式相乘时,分两个阶段:①按乘法分配律把乘积写成单项式与单项式乘积的代数和的形式;②单项式的乘法运算。几点注意:1.单项式乘多项式的结果仍是多项式,积的
项数与原多项式的项数相同。2.在单项式乘法运算中要注意系数的符号。 3.不要出现漏乘现象,运算要有顺序。解:原式= - a3b - 2a2b 2 - 5a3b+5a2b2= - 6a3b+3a2b2例3 计算:
( -2ab )3 ( 5a2b – 0.5ab2+0.25b3 )解:原式=(-8a 3 b 3) ( 5a2b – 0.5ab2+0.25b3 ) =(-8a 3 b 3) ·(5a2b) +(-8a 3 b 3) ·(- 0.5ab2 )
+(-8a 3 b 3) ·(0.25b3 ) = - 40a 5b4+4a4b 5– 2a3b6说明:先进行乘方运算,
再进行单项式与多项式的乘法运算。例4 计算:x [ x(x - 1)- 1]解法一: x [ x(x - 1)- 1] 解法二: x [ x(x - 1)- 1]= x [(x 2– x)- 1]= x (x 2– x – 1)说明:先去小括号,再去中括号。= x3 – x2 - x= x3 – x2 - x= x ? x(x - 1)- x= x2(x - 1)- x说明:先把x(x – 1)看成整体,按乘法对加法的分配律去掉中括号,再去掉小括号。几点注意:1.解题方法的灵活选择。2. 有同类项要合并。例5 解方程
7x -(x – 3)x – 3x(2 – x)=(2x + 1)x + 6解:去括号,得
7x – x 2+ 3x – 6x + 3x 2 = 2x 2 + x + 6移项,得
7x – x 2+ 3x – 6x + 3x 2 - 2x 2 - x = 6合并同类项,得 3x = 6系数化为1,得 x = 2 例6 求值:
yn(yn + 9y - 12) – 3(3yn+1 - 4yn),
其中y= - 3,n=2.解: yn(yn + 9y - 12) – 3(3yn+1 - 4yn)= y 2n+ 9yn+1- 12 yn– 9yn+1 +12 yn= y 2n当y= - 3,n=2时,原式=(- 3)4=81 求值问题,方法不是惟一
的,可以直接把字母的值代入
原式,但计算繁琐易出错,应
先化简,再代入求值,就显得
非常简捷。
例7 如图,计算图中阴影部分的面积.AB=7a,
BC=6bABCDEFGH 分析:阴影部分即长方形ABCD减去
以下四部分:梯形ADGF,△ GCF,△ AHE,
梯形HBCEABCDEFGHAB=7a,
BC=6b
解:阴影部分的面积为:小结: 单项式与多项式相乘的依据是:
乘法对加法的分配律。 单项式与多项式相乘,其积仍是多项式,项数与原多项式的项数 相同,注意不要漏乘项。 积的每一项的符号由原多项式各项符号和单项式的符号来决定,注意去括号法则。作业:实验版:
习题6.1.4 A组 1.(1,3,4,6),2.(2,3,5,6),
3.
B组 1. 2. 3.人教版:
习题7.4:A组 1.(2,5,7,8), 2.(2,3,5,6),
3.(2,4),4.
B组 1. 2.选作题:
设p = x – 1,
计算p ? (xn+xn-1+xn-2+…+x+1)
