9.5 三角形的中位线 同步练习(含答案)
文档属性
| 名称 | 9.5 三角形的中位线 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 558.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-20 11:41:49 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
9.5 三角形的中位线
知识要点:
1.连接三角形两边的_________的线段叫做三角形的中位线.
2.三角形的中位线平行于_________,并且等于第三边的__________.
补充考点(中点四边形问题):
1.顺次连接任意四边形的中点,所得到的四边形叫做原四边形的______________.
2.原四边形和中点四边形关系总结:
①中点四边形的形状取决于原四边形的_____________;
②原四边形对角线相等 中点四边形为___________;
③原四边形对角线垂直 中点四边形为___________;
3.填表:
原四边形 原四边形对角线特征 中点四边形
任意四边行
平行四边形
矩形
棱形
等腰梯形
正方形
基础练习
1.如图,已知△ABC的周长为16 cm,DE是△ABC的中位线,则△ADE的周长为( )
A.4 cm B.6 cm C.8 cm D.10 cm
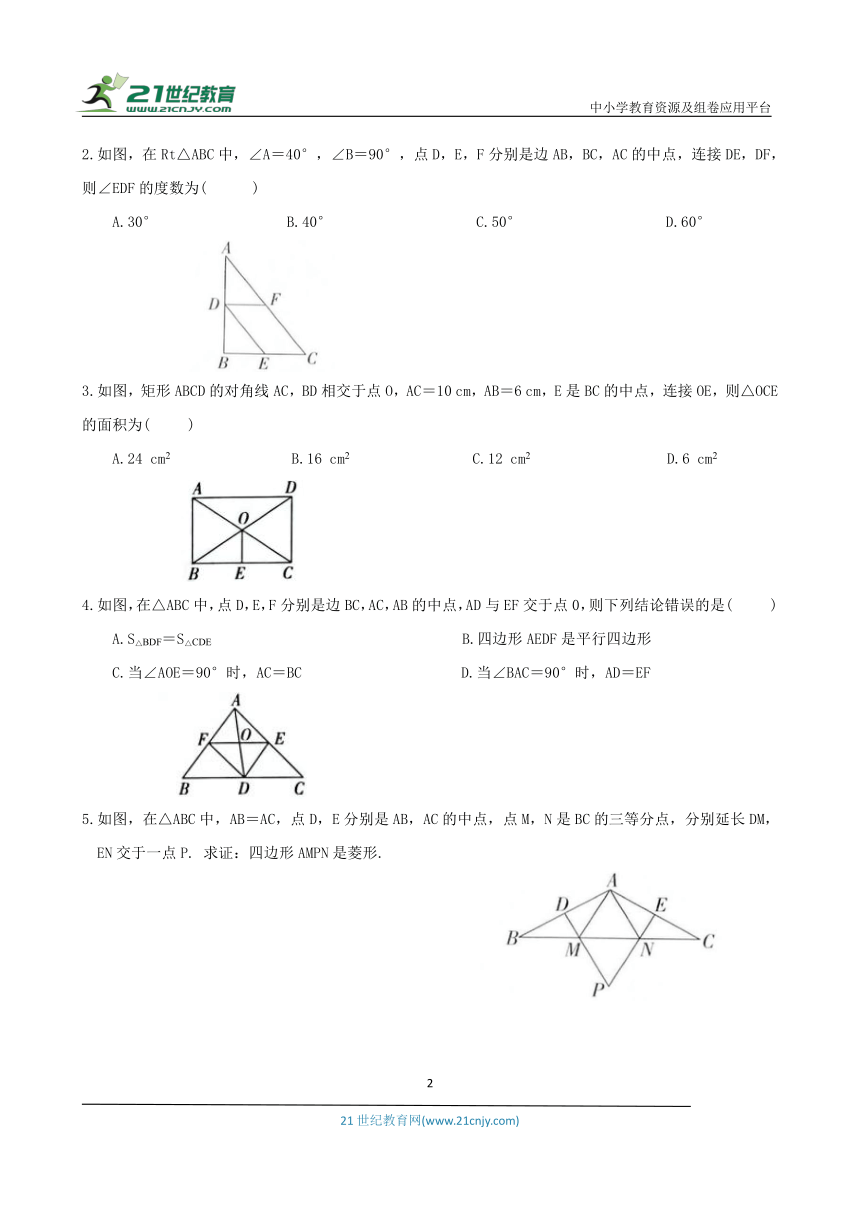
2.如图,在Rt△ABC中,∠A=40°,∠B=90°,点D,E,F分别是边AB,BC,AC的中点,连接DE,DF,则∠EDF的度数为( )
A.30° B.40° C.50° D.60°
3.如图,矩形ABCD的对角线AC,BD相交于点O,AC=10 cm,AB=6 cm,E是BC的中点,连接OE,则△OCE的面积为( )
A.24 cm2 B.16 cm2 C.12 cm2 D.6 cm2
4.如图,在△ABC中,点D,E,F分别是边BC,AC,AB的中点,AD与EF交于点0,则下列结论错误的是( )
A.S△BDF=S△CDE B.四边形AEDF是平行四边形
C.当∠AOE=90°时,AC=BC D.当∠BAC=90°时,AD=EF
5.如图,在△ABC中,AB=AC,点D,E分别是AB,AC的中点,点M,N是BC的三等分点,分别延长DM,
EN交于一点P. 求证:四边形AMPN是菱形.
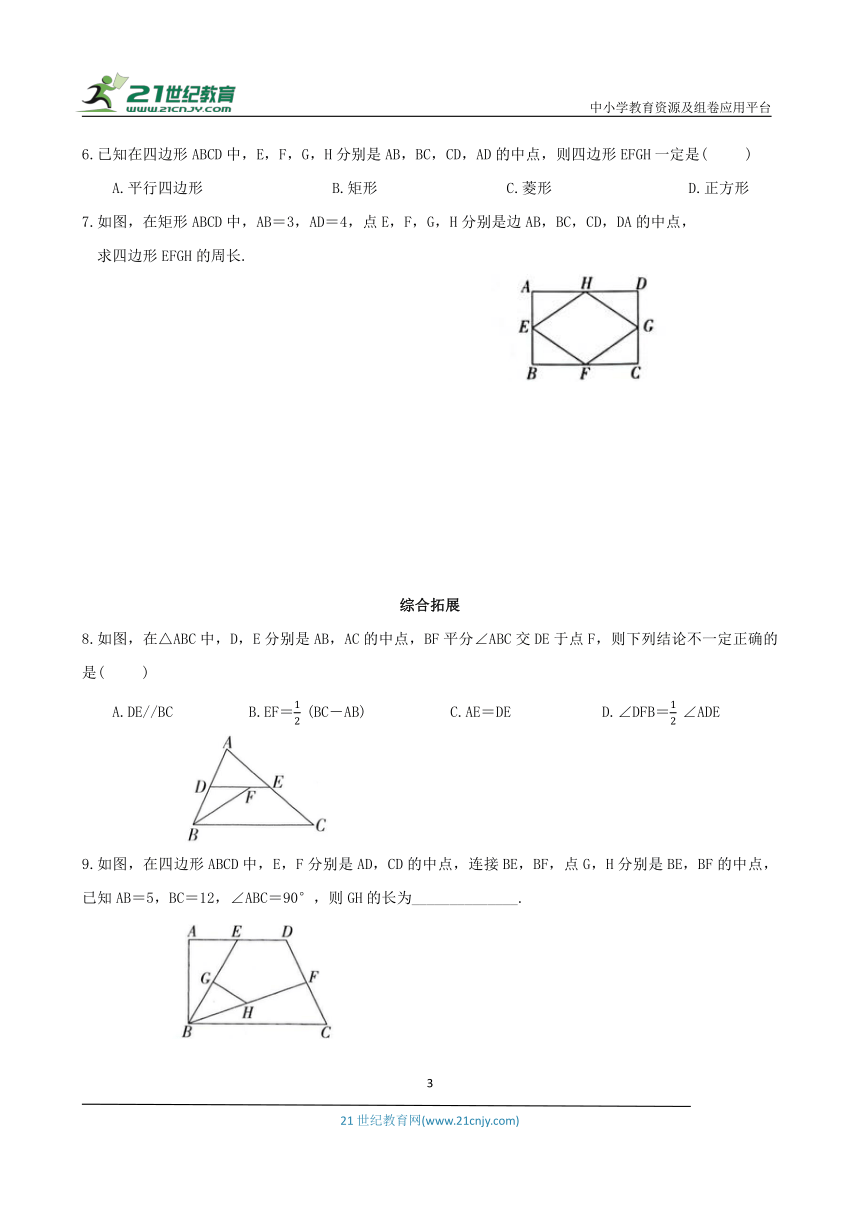
6.已知在四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD的中点,则四边形EFGH一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
7.如图,在矩形ABCD中,AB=3,AD=4,点E,F,G,H分别是边AB,BC,CD,DA的中点,
求四边形EFGH的周长.
综合拓展
8.如图,在△ABC中,D,E分别是AB,AC的中点,BF平分∠ABC交DE于点F,则下列结论不一定正确的是( )
A.DE//BC B.EF=(BC-AB) C.AE=DE D.∠DFB=∠ADE
9.如图,在四边形ABCD中,E,F分别是AD,CD的中点,连接BE,BF,点G,H分别是BE,BF的中点,已知AB=5,BC=12,∠ABC=90°,则GH的长为______________.
10.(构造三角形中位线) 如图,DE是△ABC的中位线,AQ=CN,且PQ//DE//MN,已知PQ=2,MN=4.
(1)求证:CN=QN;
(2)求BC的长.
11.(综合与实践)
知识再现:
如图①,依次连接AB,BC,CD,AD各边的中点得到四边形EFGH.
(1)四边形EFGH的形状为_______________.
问题探究:
(2)当点D在如图②所示的位置时,(1)中的结论是否成立,并写出证明过程;
(3)当点D在如图③所示的位置时,(1)中的结论还成立吗?请写出证明过程.
图① 图② 图③
参考答案
1.C
2.C
3.D
4.C
5.证明:∵点D,E分别是边AB,AC的中点,点M,N是BC的三等分点,
∴AD=BD,AE=EC,BM=MN=NC,∴DM是△ABN的中位线,EN是△ACM的中位线,
∴DM//AN,EN//AM,即MP//AN,NP//AM,∴四边形AMPN是平行四边形,
∵AB=AC,∴∠B=∠C,∴△ABM≌△ACN(SAS).∴AM=AN,∴四边形AMPN是菱形.
6.A
7.解:
如解图,连接AC,BD,
∵四边形ABCD是矩形,AB=3,AD=4,∴AC=BD==5,
∵E,F,G,H分别是边AB,BC,CD,DA的中点,
∴HG=EF=AC=,EH=FC=BD=,∴四边形EFCH的周长=×4=10
8.C
9.
10.(1)证明:∵PQ=2,MN=4,∴PQ=MN.
又∵PQ//MN.∴PQ是△AMN的中位线,∴Q是AN的中点,即AQ=QN,
∵AQ=CN,∴CN=ON;
(2)解:
∵DE是△ABC的中位线,∴DE=BC,AE=CE.
∵AQ=CN,∴AE-AQ=CE-CN,即QE=NE,
如图,连接PE并延长交MN的延长线于点O,
∵PQ//DE//MN,∴∠PQE=∠ONE,
又∵∠PEQ=∠OEN,∴△PQE≌△ONE(ASA),∴PQ=ON,PE=OE,即E为PO的中点,
∵DE//MN,∴DE是△PMO的中位线,
∵MO=2DE,即MN+ON=MN+PQ=2DE=6,∴BC=2DE=6.
11.解:(1)平行四边形;
(2)成立,
证明:
图① 图②
如解图①,连接AC,
∵E,F,G,H分别为AB,BC,CD,DA的中点,∴EF是△ABC的中位线,GH是△DAC的中位线,
∴EF/AC,ET=AC. HG/AC.NG=AC.∴EF//GH,EF=GH.∴四边形EFGH是平行四边形;
(3)成立,
证明:如解图②,连接BD,
∵E,F,G,H分别为AB,BC,CD,DA的中点,∴EH是△ABD的中位线,GF是△CBD的中位线,
∴EH∥BD,EH=BD,GF∥BD,CF=BD,∴EH//GF,EH=GF,∴四边形EFGH是平行四边形.
21世纪教育网(www.21cnjy.com)
9.5 三角形的中位线
知识要点:
1.连接三角形两边的_________的线段叫做三角形的中位线.
2.三角形的中位线平行于_________,并且等于第三边的__________.
补充考点(中点四边形问题):
1.顺次连接任意四边形的中点,所得到的四边形叫做原四边形的______________.
2.原四边形和中点四边形关系总结:
①中点四边形的形状取决于原四边形的_____________;
②原四边形对角线相等 中点四边形为___________;
③原四边形对角线垂直 中点四边形为___________;
3.填表:
原四边形 原四边形对角线特征 中点四边形
任意四边行
平行四边形
矩形
棱形
等腰梯形
正方形
基础练习
1.如图,已知△ABC的周长为16 cm,DE是△ABC的中位线,则△ADE的周长为( )
A.4 cm B.6 cm C.8 cm D.10 cm
2.如图,在Rt△ABC中,∠A=40°,∠B=90°,点D,E,F分别是边AB,BC,AC的中点,连接DE,DF,则∠EDF的度数为( )
A.30° B.40° C.50° D.60°
3.如图,矩形ABCD的对角线AC,BD相交于点O,AC=10 cm,AB=6 cm,E是BC的中点,连接OE,则△OCE的面积为( )
A.24 cm2 B.16 cm2 C.12 cm2 D.6 cm2
4.如图,在△ABC中,点D,E,F分别是边BC,AC,AB的中点,AD与EF交于点0,则下列结论错误的是( )
A.S△BDF=S△CDE B.四边形AEDF是平行四边形
C.当∠AOE=90°时,AC=BC D.当∠BAC=90°时,AD=EF
5.如图,在△ABC中,AB=AC,点D,E分别是AB,AC的中点,点M,N是BC的三等分点,分别延长DM,
EN交于一点P. 求证:四边形AMPN是菱形.
6.已知在四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD的中点,则四边形EFGH一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
7.如图,在矩形ABCD中,AB=3,AD=4,点E,F,G,H分别是边AB,BC,CD,DA的中点,
求四边形EFGH的周长.
综合拓展
8.如图,在△ABC中,D,E分别是AB,AC的中点,BF平分∠ABC交DE于点F,则下列结论不一定正确的是( )
A.DE//BC B.EF=(BC-AB) C.AE=DE D.∠DFB=∠ADE
9.如图,在四边形ABCD中,E,F分别是AD,CD的中点,连接BE,BF,点G,H分别是BE,BF的中点,已知AB=5,BC=12,∠ABC=90°,则GH的长为______________.
10.(构造三角形中位线) 如图,DE是△ABC的中位线,AQ=CN,且PQ//DE//MN,已知PQ=2,MN=4.
(1)求证:CN=QN;
(2)求BC的长.
11.(综合与实践)
知识再现:
如图①,依次连接AB,BC,CD,AD各边的中点得到四边形EFGH.
(1)四边形EFGH的形状为_______________.
问题探究:
(2)当点D在如图②所示的位置时,(1)中的结论是否成立,并写出证明过程;
(3)当点D在如图③所示的位置时,(1)中的结论还成立吗?请写出证明过程.
图① 图② 图③
参考答案
1.C
2.C
3.D
4.C
5.证明:∵点D,E分别是边AB,AC的中点,点M,N是BC的三等分点,
∴AD=BD,AE=EC,BM=MN=NC,∴DM是△ABN的中位线,EN是△ACM的中位线,
∴DM//AN,EN//AM,即MP//AN,NP//AM,∴四边形AMPN是平行四边形,
∵AB=AC,∴∠B=∠C,∴△ABM≌△ACN(SAS).∴AM=AN,∴四边形AMPN是菱形.
6.A
7.解:
如解图,连接AC,BD,
∵四边形ABCD是矩形,AB=3,AD=4,∴AC=BD==5,
∵E,F,G,H分别是边AB,BC,CD,DA的中点,
∴HG=EF=AC=,EH=FC=BD=,∴四边形EFCH的周长=×4=10
8.C
9.
10.(1)证明:∵PQ=2,MN=4,∴PQ=MN.
又∵PQ//MN.∴PQ是△AMN的中位线,∴Q是AN的中点,即AQ=QN,
∵AQ=CN,∴CN=ON;
(2)解:
∵DE是△ABC的中位线,∴DE=BC,AE=CE.
∵AQ=CN,∴AE-AQ=CE-CN,即QE=NE,
如图,连接PE并延长交MN的延长线于点O,
∵PQ//DE//MN,∴∠PQE=∠ONE,
又∵∠PEQ=∠OEN,∴△PQE≌△ONE(ASA),∴PQ=ON,PE=OE,即E为PO的中点,
∵DE//MN,∴DE是△PMO的中位线,
∵MO=2DE,即MN+ON=MN+PQ=2DE=6,∴BC=2DE=6.
11.解:(1)平行四边形;
(2)成立,
证明:
图① 图②
如解图①,连接AC,
∵E,F,G,H分别为AB,BC,CD,DA的中点,∴EF是△ABC的中位线,GH是△DAC的中位线,
∴EF/AC,ET=AC. HG/AC.NG=AC.∴EF//GH,EF=GH.∴四边形EFGH是平行四边形;
(3)成立,
证明:如解图②,连接BD,
∵E,F,G,H分别为AB,BC,CD,DA的中点,∴EH是△ABD的中位线,GF是△CBD的中位线,
∴EH∥BD,EH=BD,GF∥BD,CF=BD,∴EH//GF,EH=GF,∴四边形EFGH是平行四边形.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
