2014年海南省初中数学教师课堂教学评比资料:一次函数与方程、不等式
文档属性
| 名称 | 2014年海南省初中数学教师课堂教学评比资料:一次函数与方程、不等式 |  | |
| 格式 | zip | ||
| 文件大小 | 369.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-28 09:37:43 | ||
图片预览





文档简介
课件24张PPT。一次函数与方程、不等式(第一课时)19.2.3文昌中学:邹福新(1)解方程2x+20=0. (2)当自变量x为何值时,函数y=2x+20的值为0? 看看下面两个问题之间的关系:分析:可以从下面三个方面思考:探究一:①对于2x+20=0和y=2x+20,从形式上看,有什么不同?
②从问题的本质上看,(1)和(2)有什么关系?
③若作出y=2x+20的图像,(1)和(2)有什么关系?(1)解方程2x+20=0. (2)当自变量x为何值时,函数y=2x+20
的值为0? 问题:◆对于2x+20=0和y=2x+20,从形式上看,有什么不同?探究一:一元一次方程一次函数(1)解方程2x+20=0. 问题:探究一:◆从问题的本质上看,(1)和(2)有什么关系?(从“数”的角度看)解方程 2x+20=0,当函数值y为0时,所对应的自变量x的值.也就是:当y=0时,即2x+20=0,解得x=-10. (2)当自变量x为何值时,函数y=2x+20
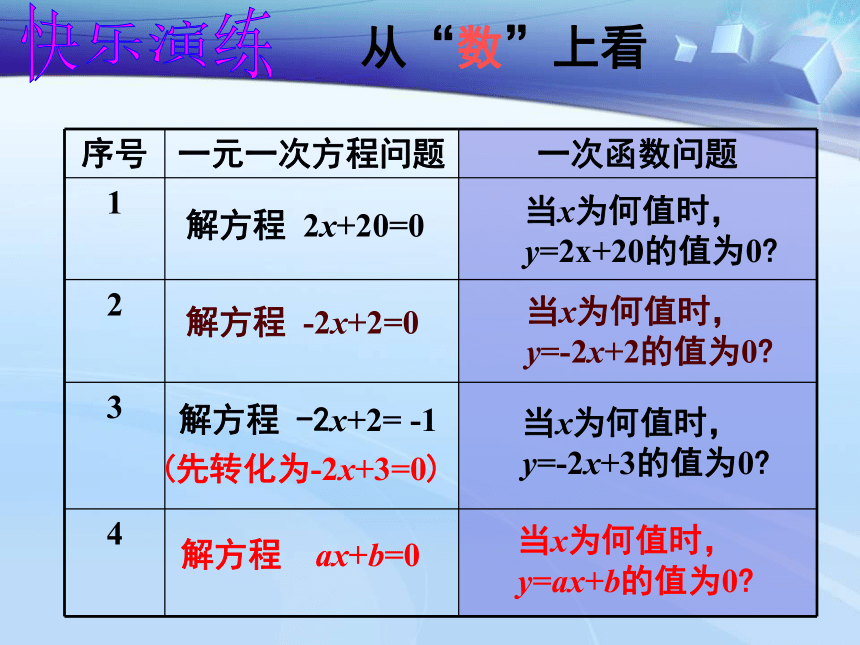
的值为0? 得x=-10.从“数”上看当x为何值时,
y=2x+20的值为0?解方程 -2x+2=0当x为何值时,
y=-2x+3的值为0?当x为何值时,
y=ax+b的值为0?解方程 ax+b=0解方程 2x+20=0解方程 -2x+2= -1当x为何值时,
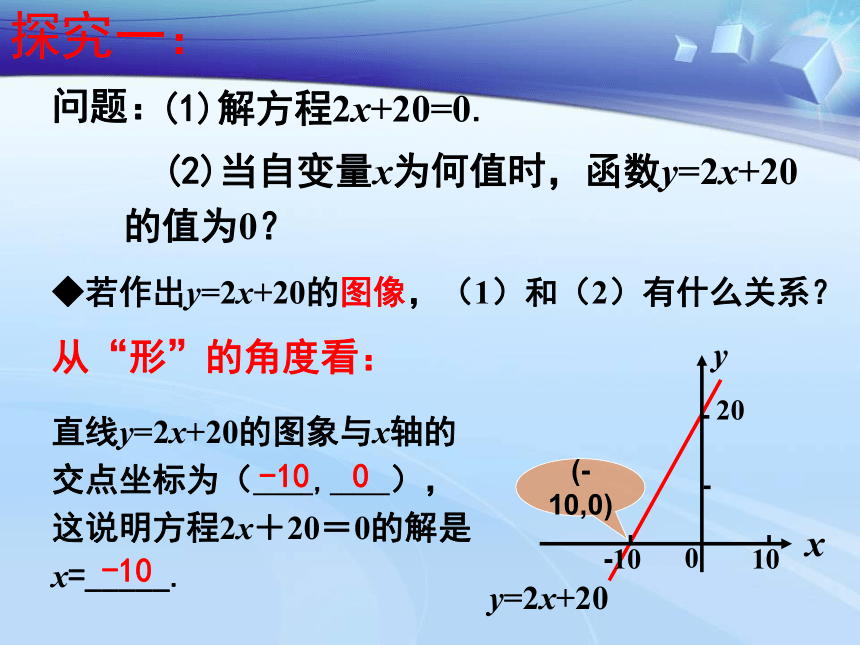
y=-2x+2的值为0?(先转化为-2x+3=0)快乐演练(1)解方程2x+20=0. 问题:探究一:◆若作出y=2x+20的图像,(1)和(2)有什么关系?从“形”的角度看:直线y=2x+20的图象与x轴的交点坐标为(_____,_____),这说明方程2x+20=0的解是x=_____.y=2x+20-100-10 (2)当自变量x为何值时,函数y=2x+20
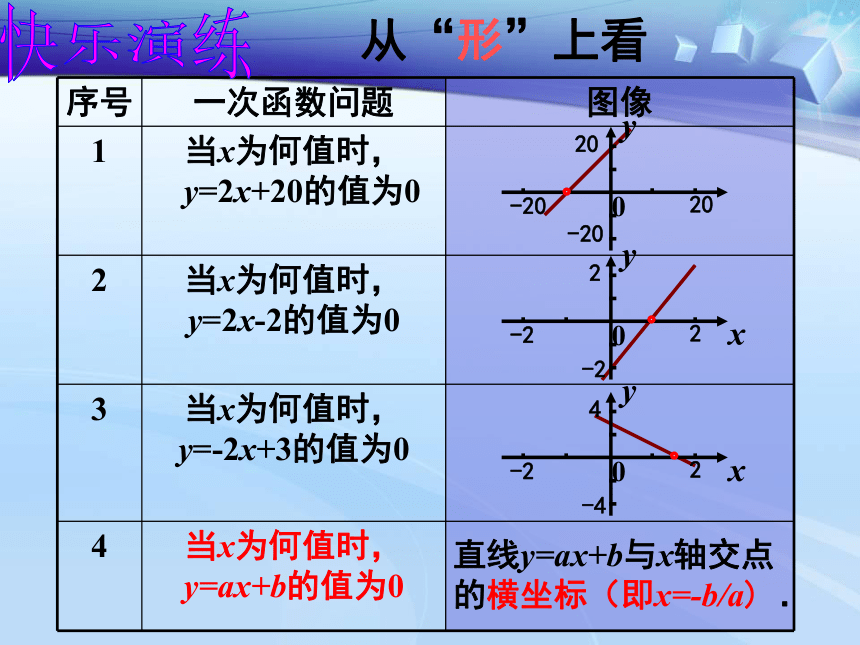
的值为0? (-10,0)从“形”上看直线y=ax+b与x轴交点
的横坐标(即x=-b/a) .快乐演练(1)解方程2x+20=0. (2)当自变量x为何值时,函数y=2x+20的值为0? 问题:探究一:结论:这两个问题实际上是同一个 问题(只是表达形式不同) 求ax+b=0(a,b是
常数,a≠0)的解.
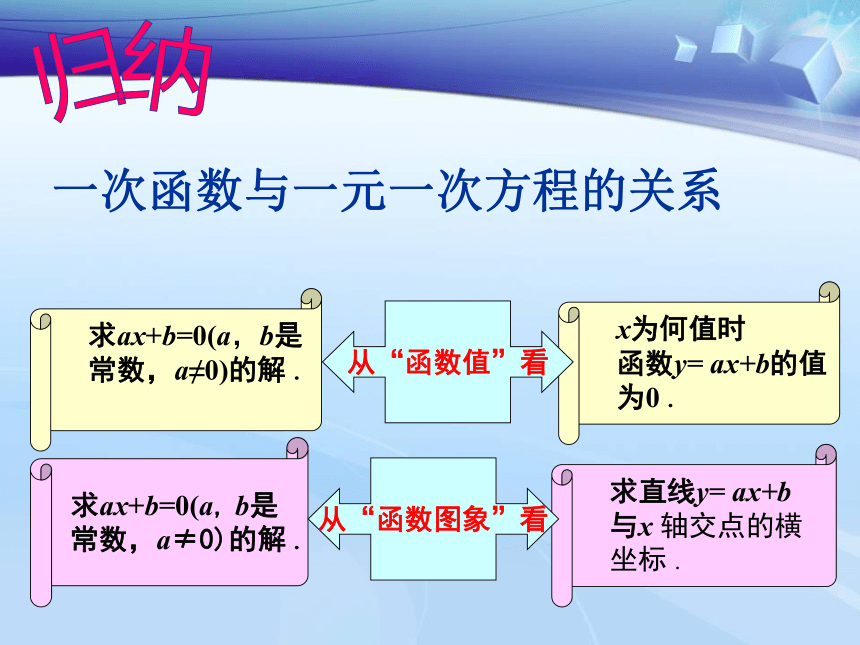
归纳一次函数与一元一次方程的关系 x为何值时
函数y= ax+b的值
为0. 从“函数值”看求ax+b=0(a, b是
常数,a≠0)的解. 求直线y= ax+b
与x 轴交点的横
坐标. 从“函数图象”看下面3个方程有什么共同点与不同点?你能从函数的角度对解这3个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.用函数的观点看:
解一元一次方程 ax+b= k就是求当函数值为k时对应的自变量x的值.2x +1=3 的解y =2x+12x +1=0 的解2x +1=-1 的解思考:求ax+b=k(a≠0)的解x为何值时,y=ax+b的值为k当函数y=ax+b纵坐标为k时,所对应的横坐标x的值求ax+b=k(a≠0)的解 (从“数”的角度)(从“形”的角度) 一次函数与一元一次方程的关系◆一元一次方程ax+b=k(a≠0)与函数y=ax+b归纳例题讲解 已知一次函数y=-2x+2,根据图像回答:
(1)当y=0时,求x的值.
(2)当y=2时,求x的值.22-2-2(1)由图像可知:一次函数y=-2x+2与x 轴的交点 为(1,0);∴当y=0时,x=1(2)由图像可知:一次函数y=-2x+2与y 轴的交点为(0,2);∴当y=2时,x=0解:根据下列图像,将一次函数转化为一元一次方程,并直接说出相应方程的解?y=5xy=-2x+4(1)(0,0)(2)(2,0)5x=0-2x+4=0快乐演练当x为何值时,y=ax+b的值?y=ax+by=ax+b快乐演练探究二:解:(1) 解得x>2
(2)就是要使2x-4>0,解得x>2时
函数y=2x-4的值大于0
(1)解不等式:2x-4>0
(2)当x为何值时,函数y=2x-4的值大于0议一议:在上面的问题解
决过程中,你能发现它们
之间有什么关系吗?从数的角度看它们是同一个问题从“数”上看根据一次函数与不等式的关系填空求一次函数y=3x-6的函数值
小于0的自变量的取值范围。
求不等式3x+8>0的解集。快乐演练(2)“当自变量x取何值时,函数y=3x+8的值大于0”可看作(2)“当自变量x取何值时,函数y=3x+8的值大于0”可看作问题3.如何用函数图象来解释:自变量x为何值时,函数y=2x-4值大于0? 解:画出直线y=2x-4,可以看出,当x>2时,这条
直线上的点在x轴的上方,
即这时y=2x-4>0
从形的角度看它们是同一个问题
从“形”上看根据下列一次函数的图像,直接写出下列不等式的解集3x+6>0(3) –x+3 ≥0(2)3x+6 ≤0X>-2(4) –x+3<0x≤3X≤-2x>3(即y>0)(即y≤0)(即y<0)(即y≥0)快乐演练一次函数与一元一次不等式的关系 求ax+b>0(或<0)(a, b
是常数,a≠0)的解集函数y=ax+b的函数值
大于0(或小于0)时x
的取值范围直线y=ax+b在X轴上方(或
下方)时自变量的取值范围从数的角度看从形的角度看 求ax+b>0(或<0)(a, b
是常数,a≠0)的解集归纳下面三个不等式有什么共同特点?你能从函数的角度对解这三个不等式进行解释吗?能把你得到的结论推广到一般情形吗?
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1. 不等式ax+b>c的解集就是
使函数y =ax+b 的函数值大于c
的对应的自变量取值范围;
不等式ax+b<c的解集就是
使函数y =ax+b 的函数值小于c
的对应的自变量取值范围.y =3x+2y =2y =0y =-1思考:x>21.如图是一次函数的图象,则关于x的方程的解为 ;关于x的不等式的解集为 ;的解集为 .关于x的不等式x=2x<2快乐演练谈谈你的收获与困惑?反思提高作业习题19.2.3 第1题谢谢!请各位领导老师给予点评和指正!
②从问题的本质上看,(1)和(2)有什么关系?
③若作出y=2x+20的图像,(1)和(2)有什么关系?(1)解方程2x+20=0. (2)当自变量x为何值时,函数y=2x+20
的值为0? 问题:◆对于2x+20=0和y=2x+20,从形式上看,有什么不同?探究一:一元一次方程一次函数(1)解方程2x+20=0. 问题:探究一:◆从问题的本质上看,(1)和(2)有什么关系?(从“数”的角度看)解方程 2x+20=0,当函数值y为0时,所对应的自变量x的值.也就是:当y=0时,即2x+20=0,解得x=-10. (2)当自变量x为何值时,函数y=2x+20
的值为0? 得x=-10.从“数”上看当x为何值时,
y=2x+20的值为0?解方程 -2x+2=0当x为何值时,
y=-2x+3的值为0?当x为何值时,
y=ax+b的值为0?解方程 ax+b=0解方程 2x+20=0解方程 -2x+2= -1当x为何值时,
y=-2x+2的值为0?(先转化为-2x+3=0)快乐演练(1)解方程2x+20=0. 问题:探究一:◆若作出y=2x+20的图像,(1)和(2)有什么关系?从“形”的角度看:直线y=2x+20的图象与x轴的交点坐标为(_____,_____),这说明方程2x+20=0的解是x=_____.y=2x+20-100-10 (2)当自变量x为何值时,函数y=2x+20
的值为0? (-10,0)从“形”上看直线y=ax+b与x轴交点
的横坐标(即x=-b/a) .快乐演练(1)解方程2x+20=0. (2)当自变量x为何值时,函数y=2x+20的值为0? 问题:探究一:结论:这两个问题实际上是同一个 问题(只是表达形式不同) 求ax+b=0(a,b是
常数,a≠0)的解.
归纳一次函数与一元一次方程的关系 x为何值时
函数y= ax+b的值
为0. 从“函数值”看求ax+b=0(a, b是
常数,a≠0)的解. 求直线y= ax+b
与x 轴交点的横
坐标. 从“函数图象”看下面3个方程有什么共同点与不同点?你能从函数的角度对解这3个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.用函数的观点看:
解一元一次方程 ax+b= k就是求当函数值为k时对应的自变量x的值.2x +1=3 的解y =2x+12x +1=0 的解2x +1=-1 的解思考:求ax+b=k(a≠0)的解x为何值时,y=ax+b的值为k当函数y=ax+b纵坐标为k时,所对应的横坐标x的值求ax+b=k(a≠0)的解 (从“数”的角度)(从“形”的角度) 一次函数与一元一次方程的关系◆一元一次方程ax+b=k(a≠0)与函数y=ax+b归纳例题讲解 已知一次函数y=-2x+2,根据图像回答:
(1)当y=0时,求x的值.
(2)当y=2时,求x的值.22-2-2(1)由图像可知:一次函数y=-2x+2与x 轴的交点 为(1,0);∴当y=0时,x=1(2)由图像可知:一次函数y=-2x+2与y 轴的交点为(0,2);∴当y=2时,x=0解:根据下列图像,将一次函数转化为一元一次方程,并直接说出相应方程的解?y=5xy=-2x+4(1)(0,0)(2)(2,0)5x=0-2x+4=0快乐演练当x为何值时,y=ax+b的值?y=ax+by=ax+b快乐演练探究二:解:(1) 解得x>2
(2)就是要使2x-4>0,解得x>2时
函数y=2x-4的值大于0
(1)解不等式:2x-4>0
(2)当x为何值时,函数y=2x-4的值大于0议一议:在上面的问题解
决过程中,你能发现它们
之间有什么关系吗?从数的角度看它们是同一个问题从“数”上看根据一次函数与不等式的关系填空求一次函数y=3x-6的函数值
小于0的自变量的取值范围。
求不等式3x+8>0的解集。快乐演练(2)“当自变量x取何值时,函数y=3x+8的值大于0”可看作(2)“当自变量x取何值时,函数y=3x+8的值大于0”可看作问题3.如何用函数图象来解释:自变量x为何值时,函数y=2x-4值大于0? 解:画出直线y=2x-4,可以看出,当x>2时,这条
直线上的点在x轴的上方,
即这时y=2x-4>0
从形的角度看它们是同一个问题
从“形”上看根据下列一次函数的图像,直接写出下列不等式的解集3x+6>0(3) –x+3 ≥0(2)3x+6 ≤0X>-2(4) –x+3<0x≤3X≤-2x>3(即y>0)(即y≤0)(即y<0)(即y≥0)快乐演练一次函数与一元一次不等式的关系 求ax+b>0(或<0)(a, b
是常数,a≠0)的解集函数y=ax+b的函数值
大于0(或小于0)时x
的取值范围直线y=ax+b在X轴上方(或
下方)时自变量的取值范围从数的角度看从形的角度看 求ax+b>0(或<0)(a, b
是常数,a≠0)的解集归纳下面三个不等式有什么共同特点?你能从函数的角度对解这三个不等式进行解释吗?能把你得到的结论推广到一般情形吗?
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1. 不等式ax+b>c的解集就是
使函数y =ax+b 的函数值大于c
的对应的自变量取值范围;
不等式ax+b<c的解集就是
使函数y =ax+b 的函数值小于c
的对应的自变量取值范围.y =3x+2y =2y =0y =-1思考:x>21.如图是一次函数的图象,则关于x的方程的解为 ;关于x的不等式的解集为 ;的解集为 .关于x的不等式x=2x<2快乐演练谈谈你的收获与困惑?反思提高作业习题19.2.3 第1题谢谢!请各位领导老师给予点评和指正!
