人教版初中数学七年级下册教学设计 7.1.2 平面直角坐标系
文档属性
| 名称 | 人教版初中数学七年级下册教学设计 7.1.2 平面直角坐标系 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 09:34:51 | ||
图片预览


文档简介
人教版初中数学七年级下册
7.1.2 平面直角坐标系 教学设计
一、教学目标:
1.理解平面直角坐标系以及横轴、纵轴、原点、坐标等概念,认识并能画出平面直角坐标系;
2.理解各象限内及坐标轴上点的坐标特征;
3.会用象限或坐标轴说明直角坐标系内点的位置,能根据横、纵坐标的符号确定点的位置.
二、教学重、难点:
重点:平面直角坐标系和点的坐标,描出点的位置和建立坐标系.
难点:根据点的位置写出点的坐标,适当地建立坐标系.
三、教学过程:
复习回顾
1.在平面内,确定物体的位置一般需要几个数据?有哪些方法?
在平面内,确定物体的位置一般需要两个数据.
常用的方法:用有序数对来确定,如:(排,列),(组,排),(排,号),(角度,距离),(经度,纬度)等.
2.什么是数轴?
规定了原点、正方向、单位长度的直线就构成了数轴.
数轴上的点A表示数1. 反过来,数1就是点A的位置. 我们说数1是点A在数轴上的坐标.
同理可知,点B在数轴上的坐标是____;点C在数轴上的坐标是____;点D在数轴上坐标是____.
数轴上的点与实数之间存在着__________的关系.
知识精讲
思考:类似于利用数轴确定直线上点的位置,能不能找到一种方法来确定平面内的点的位置呢?(例如:下图中A、B、C、D各点)
如图,我们可以在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系. 水平的数轴称为x轴或横轴,习惯上取向右为正方向;竖直的数轴称为y轴或纵轴,取向上方
向为正方向;两坐标轴的交点为平面直角坐标系的原点.
有了,平面直角坐标系,平面内的点就可以用一个有序数对来表示了.
例如,由点A分别向x轴和y轴作垂线,垂足M在x轴上的坐标是3,垂足N在y轴上的坐标是4,我们说点A的横坐标是3,纵坐标是4,有序数对(3,4)就叫做点A的坐标,记作A(3,4).
类似地,请你写出点B,C,D的坐标:
思考:原点O的坐标是什么?x轴和y轴上的点的坐标有什么特点?
原点O的坐标为(0,0);x 轴上的点的纵坐标为0,例如(1,0),(-1,0),…;y 轴上的点的横坐标为0,例如(0,1),(0,-1),….如右上图A(3,0),B(-2,0) ,C(0,2),D(0,-3).
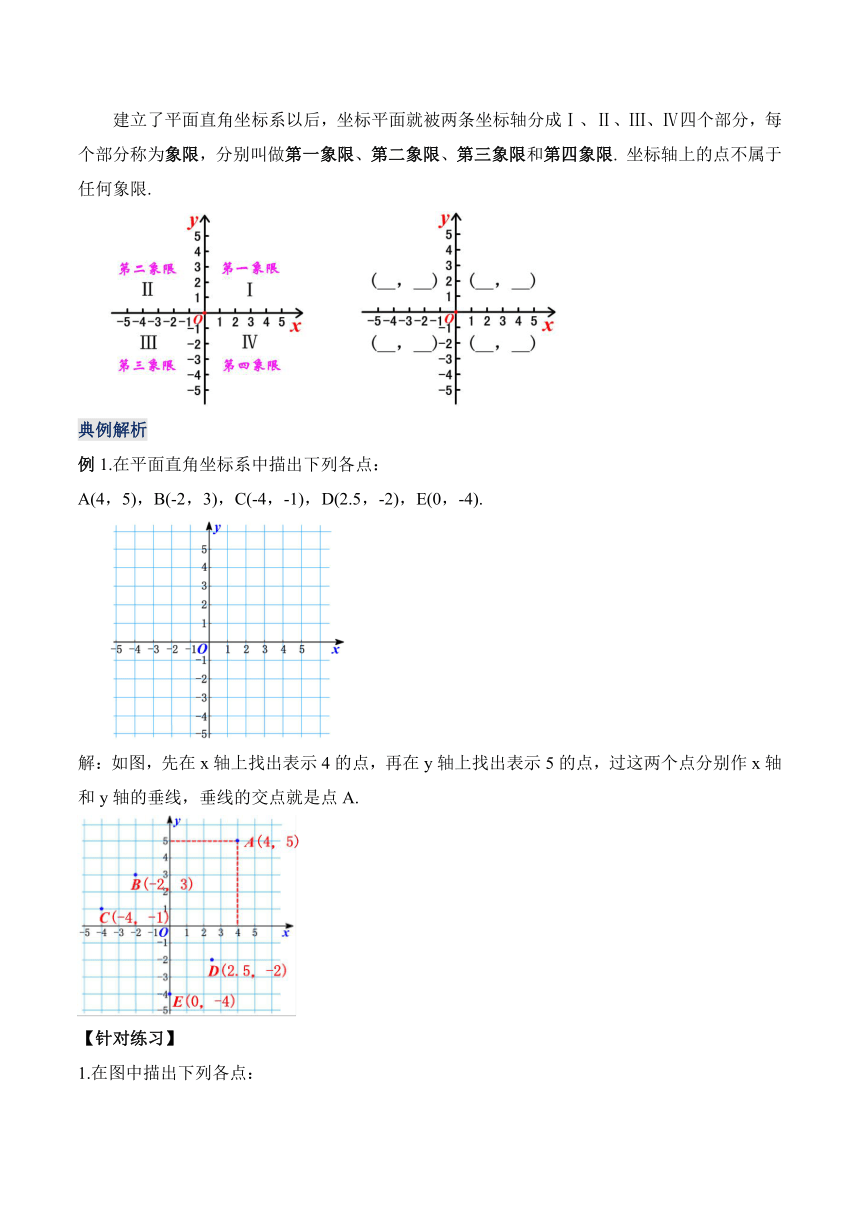
建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分,每个部分称为象限,分别叫做第一象限、第二象限、第三象限和第四象限. 坐标轴上的点不属于任何象限.
典例解析
例1.在平面直角坐标系中描出下列各点:
A(4,5),B(-2,3),C(-4,-1),D(2.5,-2),E(0,-4).
解:如图,先在x轴上找出表示4的点,再在y轴上找出表示5的点,过这两个点分别作x轴和y轴的垂线,垂线的交点就是点A.
【针对练习】
1.在图中描出下列各点:
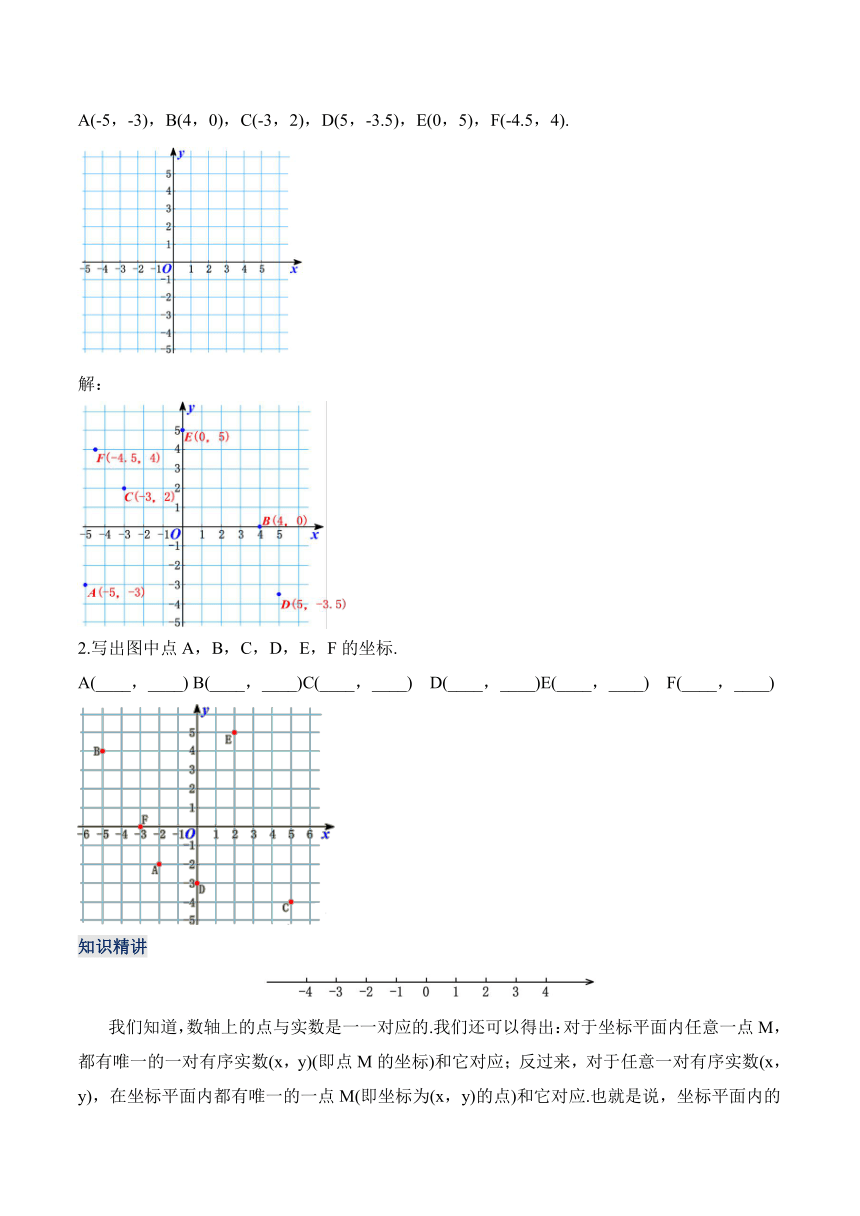
A(-5,-3),B(4,0),C(-3,2),D(5,-3.5),E(0,5),F(-4.5,4).
解:
2.写出图中点A,B,C,D,E,F的坐标.
A(____,____) B(____,____)C(____,____) D(____,____)E(____,____) F(____,____)
知识精讲
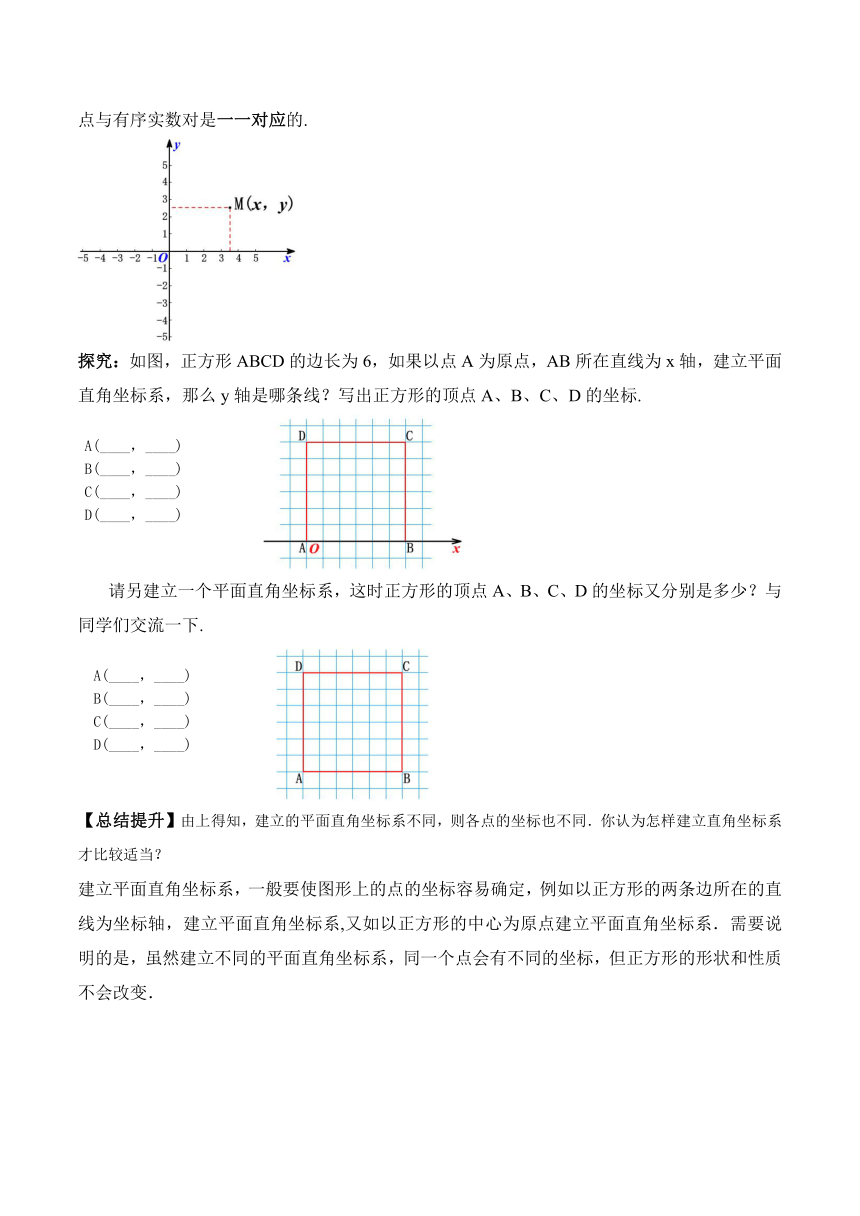
我们知道,数轴上的点与实数是一一对应的.我们还可以得出:对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)(即点M的坐标)和它对应;反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.也就是说,坐标平面内的点与有序实数对是一一对应的.
探究:如图,正方形ABCD的边长为6,如果以点A为原点,AB所在直线为x轴,建立平面直角坐标系,那么y轴是哪条线?写出正方形的顶点A、B、C、D的坐标.
请另建立一个平面直角坐标系,这时正方形的顶点A、B、C、D的坐标又分别是多少?与同学们交流一下.
【总结提升】由上得知,建立的平面直角坐标系不同,则各点的坐标也不同.你认为怎样建立直角坐标系才比较适当?
建立平面直角坐标系,一般要使图形上的点的坐标容易确定,例如以正方形的两条边所在的直线为坐标轴,建立平面直角坐标系,又如以正方形的中心为原点建立平面直角坐标系.需要说明的是,虽然建立不同的平面直角坐标系,同一个点会有不同的坐标,但正方形的形状和性质不会改变.
典例解析
例2.长方形的两条边长分别为4,6,建立适当的直角坐标系,使它的一个顶点的坐标为(-2,-3).请你写出另外三个顶点的坐标.
解:如图, 建立直角坐标系,
∵长方形的一个顶点的坐标为A(-2,-3),
∴长方形的另外三个顶点的坐标分别为B(2,-3),C(2,3),D(-2,3).
你还有其它的做法吗?
【针对练习】右图是一个围棋棋盘(局部),把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(-2,-1),白棋③的坐标是(-1,-3),则黑棋 的坐标是_____.
【分析】由已知白棋①的坐标是(-2,-1),白棋③的坐标是(-1,-3),可知y轴应在从左往右数的第四条格线上,且向上为正方向;x轴在从上往下数第二条格线上,且向右为正方向;这两条直线的交点为坐标原点,由此可得黑棋②的坐标是(1,-2).
例3.设点M(a,b)为平面直角坐标系内的点.
(1)当a>0,b<0时,点M位于第几象限?
(2)当ab>0时,点M位于第几象限?
(3)当a为任意有理数,且b<0时,点M位于第几象限?
解:(1)点M在第四象限;
(2)在第一象限(a>0,b>0)或者在第三象限(a<0,b<0);
(3)在第三象限(a<0,b<0)或者第四象限(a>0,b<0)或者y轴负半轴上(a=0,b<0).
【针对练习】点A(m+3,m+1)在x轴上,则A点的坐标为( )
A.(0,-2) B.(2,0) C.(4,0) D.(0,-4)
【分析】点A(m+3,m+1)在x轴上,根据x轴上点的坐标特征知m+1=0,求出m的值代入m+3中即可.
例4.已知点与点在同一条平行于轴的直线上,且点到轴的距离为5,求点的坐标.
解:∵点与点在同一条平行于轴的直线上,
∴.
∵点到轴的距离为5,
∴.
∴,
∴点的坐标为或.
【针对练习】已知平面直角坐标系中有一点
(1)点M到x轴的距离为1时,M的坐标?
(2)点且轴时,M的坐标?
解:(1)∵点,点M到x轴的距离为1,
∴,
解得,或,
当时,点M的坐标为,
当时,点M的坐标为;
(2)∵点,点且轴,
∴,
解得,,
故点M的坐标为.
例5.如图所示,在平面直角坐标系中,一动点从原点出发,按向上、向右、向下、向右的方向不断移动,每次移动一个单位,得到点,,,,,那么点的坐标为( )
A. B. C. D.
【分析】根据题意,观察图形可知:,
(为自然数),
,,
,
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
【设计意图】培养学生概括的能力。使知识形成体系,并渗透数学思想方法。
达标检测
1.下列各点中,在第二象限的点是( )
A.(2,3) B.(2,-3) C.(-2,3) D.(-2,-3)
2.点P在第三象限内,P到x轴的距离是4,到y轴的距离是3,那么点P的坐标是( )
A.(-4,3) B.(-3,-4) C.(-3,4) D.(3,-4)
3.已知点A(0,100),B(200,0),C(0,0),D(-200,0),E(-50,0),则在x轴上的点有( )
A.1个 B.2个 C.3个 D.4个
4.若点M(a,b)的坐标满足ab<0,则点M在( )
A.第一象限 B.第一象限或第三象限
C.第二象限 D.第二象限或第四象限
5.若点P(x, y)在第四象限,且|x|=5, |y|=6,则点P的坐标是( )
A.(-5,-6) B.(-5,6) C.(5,-6) D.(5,6)
6.已知点A(2,-3), AB⊥y轴,B为垂足,则B点的坐标为( )
A.(0,-3) B.(-3,0) C.(0,2) D.(0,0)
7.下列语句:①点(3,2)与点(2,3)是同一个点;②点(0,1)在x轴上;③点(0,0)是坐标原点;④点(2,-1)在第四象限内.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
8.指出下列各点所在的象限或坐标轴:
A(-1,-2.5)在___________; B(3,-4)在___________;
C(-,5)在___________; D(7,9)在___________;
E(-π,0)在___________; F(0,)在___________.
9.点P(-5,7)到x轴的距离是_____,到y轴的距离是_____.
10.在直角坐标系中,已知点A的坐标为(-3,2),点B的坐标为(5,2), 连接A,B两点所成线段与_______平行.
11.如果点M(-5,2+b)在x轴上,则b=______.
12.如果点N(a-3,2a)在y轴上,则点N的坐标是__________.
13.如图,点A的坐标是________,点B的坐标是_________,点C的坐标是_________,点D的坐标是__________,点E的坐标是__________,点F的坐标是________,点G的坐标是________,点H的坐标是________.
14.已知点,若点的纵坐标比横坐标大6,求点到轴和轴的距离.
15.中国象棋盘中蕴含着直角坐标系,下图是中国象棋棋盘的一半,棋子“馬”走的规则是沿“日”形的对角线走,例如图中“馬”可以直接走到A、B等处.若“馬”的位置在C点,为了到达D点,请按“馬”走的规则,在图中的棋盘上用虚线画出一种你认为合理的行走路线;并建立适当的平面直角坐标系,用坐标表示它的行走路线.
【参考答案】
C
B
D
D
C
A
C
第三象限;第四象限;第二象限;第一象限;x轴;y轴
7,5
X轴
-2
(0,6)
(-2,4);(-4,2);(-4,-2);(-2,-4);(2,-4);(4,-2);(4, 2);(2,4).
14.解:∵点的纵坐标比横坐标大6,
∴,
解得,
∴,,
∴点的坐标为,
所以点到轴的距离为4,到轴的距离为2.
15解:如图“馬”行走路线的坐标为C(1,2)→(2,0)→(0,1)→(2,2)→D(3,0).
四、教学反思:
通过平面直角坐标系的有关内容的学习,反映平面直角坐标系与现实世界的密切联系,让学生认识数学与人类生活的密切联系和对人类历史发展的作用,提高学生学习数学的积极性和好奇心.
7.1.2 平面直角坐标系 教学设计
一、教学目标:
1.理解平面直角坐标系以及横轴、纵轴、原点、坐标等概念,认识并能画出平面直角坐标系;
2.理解各象限内及坐标轴上点的坐标特征;
3.会用象限或坐标轴说明直角坐标系内点的位置,能根据横、纵坐标的符号确定点的位置.
二、教学重、难点:
重点:平面直角坐标系和点的坐标,描出点的位置和建立坐标系.
难点:根据点的位置写出点的坐标,适当地建立坐标系.
三、教学过程:
复习回顾
1.在平面内,确定物体的位置一般需要几个数据?有哪些方法?
在平面内,确定物体的位置一般需要两个数据.
常用的方法:用有序数对来确定,如:(排,列),(组,排),(排,号),(角度,距离),(经度,纬度)等.
2.什么是数轴?
规定了原点、正方向、单位长度的直线就构成了数轴.
数轴上的点A表示数1. 反过来,数1就是点A的位置. 我们说数1是点A在数轴上的坐标.
同理可知,点B在数轴上的坐标是____;点C在数轴上的坐标是____;点D在数轴上坐标是____.
数轴上的点与实数之间存在着__________的关系.
知识精讲
思考:类似于利用数轴确定直线上点的位置,能不能找到一种方法来确定平面内的点的位置呢?(例如:下图中A、B、C、D各点)
如图,我们可以在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系. 水平的数轴称为x轴或横轴,习惯上取向右为正方向;竖直的数轴称为y轴或纵轴,取向上方
向为正方向;两坐标轴的交点为平面直角坐标系的原点.
有了,平面直角坐标系,平面内的点就可以用一个有序数对来表示了.
例如,由点A分别向x轴和y轴作垂线,垂足M在x轴上的坐标是3,垂足N在y轴上的坐标是4,我们说点A的横坐标是3,纵坐标是4,有序数对(3,4)就叫做点A的坐标,记作A(3,4).
类似地,请你写出点B,C,D的坐标:
思考:原点O的坐标是什么?x轴和y轴上的点的坐标有什么特点?
原点O的坐标为(0,0);x 轴上的点的纵坐标为0,例如(1,0),(-1,0),…;y 轴上的点的横坐标为0,例如(0,1),(0,-1),….如右上图A(3,0),B(-2,0) ,C(0,2),D(0,-3).
建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分,每个部分称为象限,分别叫做第一象限、第二象限、第三象限和第四象限. 坐标轴上的点不属于任何象限.
典例解析
例1.在平面直角坐标系中描出下列各点:
A(4,5),B(-2,3),C(-4,-1),D(2.5,-2),E(0,-4).
解:如图,先在x轴上找出表示4的点,再在y轴上找出表示5的点,过这两个点分别作x轴和y轴的垂线,垂线的交点就是点A.
【针对练习】
1.在图中描出下列各点:
A(-5,-3),B(4,0),C(-3,2),D(5,-3.5),E(0,5),F(-4.5,4).
解:
2.写出图中点A,B,C,D,E,F的坐标.
A(____,____) B(____,____)C(____,____) D(____,____)E(____,____) F(____,____)
知识精讲
我们知道,数轴上的点与实数是一一对应的.我们还可以得出:对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)(即点M的坐标)和它对应;反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.也就是说,坐标平面内的点与有序实数对是一一对应的.
探究:如图,正方形ABCD的边长为6,如果以点A为原点,AB所在直线为x轴,建立平面直角坐标系,那么y轴是哪条线?写出正方形的顶点A、B、C、D的坐标.
请另建立一个平面直角坐标系,这时正方形的顶点A、B、C、D的坐标又分别是多少?与同学们交流一下.
【总结提升】由上得知,建立的平面直角坐标系不同,则各点的坐标也不同.你认为怎样建立直角坐标系才比较适当?
建立平面直角坐标系,一般要使图形上的点的坐标容易确定,例如以正方形的两条边所在的直线为坐标轴,建立平面直角坐标系,又如以正方形的中心为原点建立平面直角坐标系.需要说明的是,虽然建立不同的平面直角坐标系,同一个点会有不同的坐标,但正方形的形状和性质不会改变.
典例解析
例2.长方形的两条边长分别为4,6,建立适当的直角坐标系,使它的一个顶点的坐标为(-2,-3).请你写出另外三个顶点的坐标.
解:如图, 建立直角坐标系,
∵长方形的一个顶点的坐标为A(-2,-3),
∴长方形的另外三个顶点的坐标分别为B(2,-3),C(2,3),D(-2,3).
你还有其它的做法吗?
【针对练习】右图是一个围棋棋盘(局部),把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(-2,-1),白棋③的坐标是(-1,-3),则黑棋 的坐标是_____.
【分析】由已知白棋①的坐标是(-2,-1),白棋③的坐标是(-1,-3),可知y轴应在从左往右数的第四条格线上,且向上为正方向;x轴在从上往下数第二条格线上,且向右为正方向;这两条直线的交点为坐标原点,由此可得黑棋②的坐标是(1,-2).
例3.设点M(a,b)为平面直角坐标系内的点.
(1)当a>0,b<0时,点M位于第几象限?
(2)当ab>0时,点M位于第几象限?
(3)当a为任意有理数,且b<0时,点M位于第几象限?
解:(1)点M在第四象限;
(2)在第一象限(a>0,b>0)或者在第三象限(a<0,b<0);
(3)在第三象限(a<0,b<0)或者第四象限(a>0,b<0)或者y轴负半轴上(a=0,b<0).
【针对练习】点A(m+3,m+1)在x轴上,则A点的坐标为( )
A.(0,-2) B.(2,0) C.(4,0) D.(0,-4)
【分析】点A(m+3,m+1)在x轴上,根据x轴上点的坐标特征知m+1=0,求出m的值代入m+3中即可.
例4.已知点与点在同一条平行于轴的直线上,且点到轴的距离为5,求点的坐标.
解:∵点与点在同一条平行于轴的直线上,
∴.
∵点到轴的距离为5,
∴.
∴,
∴点的坐标为或.
【针对练习】已知平面直角坐标系中有一点
(1)点M到x轴的距离为1时,M的坐标?
(2)点且轴时,M的坐标?
解:(1)∵点,点M到x轴的距离为1,
∴,
解得,或,
当时,点M的坐标为,
当时,点M的坐标为;
(2)∵点,点且轴,
∴,
解得,,
故点M的坐标为.
例5.如图所示,在平面直角坐标系中,一动点从原点出发,按向上、向右、向下、向右的方向不断移动,每次移动一个单位,得到点,,,,,那么点的坐标为( )
A. B. C. D.
【分析】根据题意,观察图形可知:,
(为自然数),
,,
,
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
【设计意图】培养学生概括的能力。使知识形成体系,并渗透数学思想方法。
达标检测
1.下列各点中,在第二象限的点是( )
A.(2,3) B.(2,-3) C.(-2,3) D.(-2,-3)
2.点P在第三象限内,P到x轴的距离是4,到y轴的距离是3,那么点P的坐标是( )
A.(-4,3) B.(-3,-4) C.(-3,4) D.(3,-4)
3.已知点A(0,100),B(200,0),C(0,0),D(-200,0),E(-50,0),则在x轴上的点有( )
A.1个 B.2个 C.3个 D.4个
4.若点M(a,b)的坐标满足ab<0,则点M在( )
A.第一象限 B.第一象限或第三象限
C.第二象限 D.第二象限或第四象限
5.若点P(x, y)在第四象限,且|x|=5, |y|=6,则点P的坐标是( )
A.(-5,-6) B.(-5,6) C.(5,-6) D.(5,6)
6.已知点A(2,-3), AB⊥y轴,B为垂足,则B点的坐标为( )
A.(0,-3) B.(-3,0) C.(0,2) D.(0,0)
7.下列语句:①点(3,2)与点(2,3)是同一个点;②点(0,1)在x轴上;③点(0,0)是坐标原点;④点(2,-1)在第四象限内.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
8.指出下列各点所在的象限或坐标轴:
A(-1,-2.5)在___________; B(3,-4)在___________;
C(-,5)在___________; D(7,9)在___________;
E(-π,0)在___________; F(0,)在___________.
9.点P(-5,7)到x轴的距离是_____,到y轴的距离是_____.
10.在直角坐标系中,已知点A的坐标为(-3,2),点B的坐标为(5,2), 连接A,B两点所成线段与_______平行.
11.如果点M(-5,2+b)在x轴上,则b=______.
12.如果点N(a-3,2a)在y轴上,则点N的坐标是__________.
13.如图,点A的坐标是________,点B的坐标是_________,点C的坐标是_________,点D的坐标是__________,点E的坐标是__________,点F的坐标是________,点G的坐标是________,点H的坐标是________.
14.已知点,若点的纵坐标比横坐标大6,求点到轴和轴的距离.
15.中国象棋盘中蕴含着直角坐标系,下图是中国象棋棋盘的一半,棋子“馬”走的规则是沿“日”形的对角线走,例如图中“馬”可以直接走到A、B等处.若“馬”的位置在C点,为了到达D点,请按“馬”走的规则,在图中的棋盘上用虚线画出一种你认为合理的行走路线;并建立适当的平面直角坐标系,用坐标表示它的行走路线.
【参考答案】
C
B
D
D
C
A
C
第三象限;第四象限;第二象限;第一象限;x轴;y轴
7,5
X轴
-2
(0,6)
(-2,4);(-4,2);(-4,-2);(-2,-4);(2,-4);(4,-2);(4, 2);(2,4).
14.解:∵点的纵坐标比横坐标大6,
∴,
解得,
∴,,
∴点的坐标为,
所以点到轴的距离为4,到轴的距离为2.
15解:如图“馬”行走路线的坐标为C(1,2)→(2,0)→(0,1)→(2,2)→D(3,0).
四、教学反思:
通过平面直角坐标系的有关内容的学习,反映平面直角坐标系与现实世界的密切联系,让学生认识数学与人类生活的密切联系和对人类历史发展的作用,提高学生学习数学的积极性和好奇心.
