3.2.2《图形的旋转》北师大版八年级数学下册 课时作业(含答案)
文档属性
| 名称 | 3.2.2《图形的旋转》北师大版八年级数学下册 课时作业(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 201.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 09:50:11 | ||
图片预览


文档简介
3.2 图形的旋转(2)
一、选择题
1.下列物体的运动不是旋转的是( )
A.运转的摩天轮上的一只灯泡 B.正在走动的时针
C.骑自行车的人 D.正在转动的风车叶片
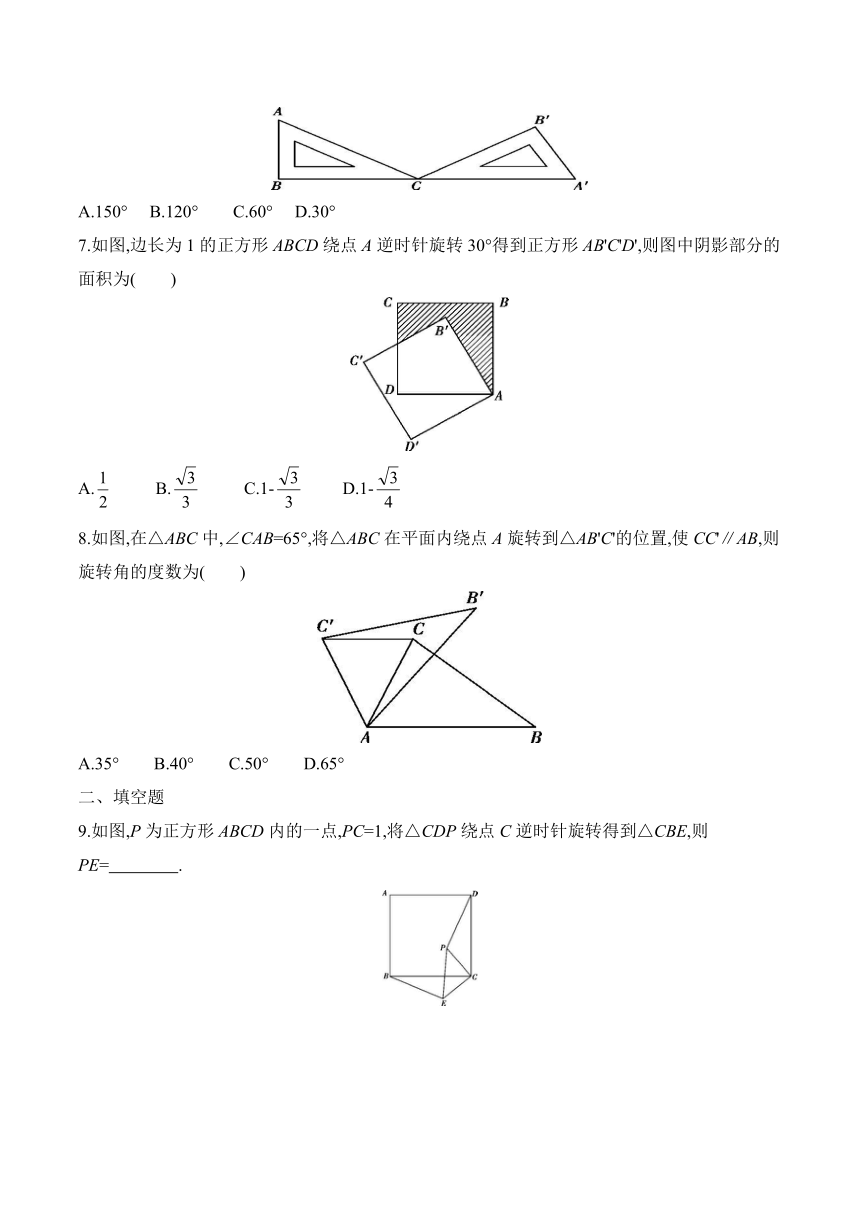
2.如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A'B'C,连接AB',若AB'=3,则∠A'的度数为( )
A.125° B.130° C.135° D.140°
3.若点A的坐标为(6,3),O为坐标原点,将OA绕点O按顺时针方向旋转90°得到OA',则点A'的坐标是( )
A.(3,-6) B.(-3,6) C.(-3,-6) D.(3,6)
4.如图,方格纸上的△DEF是由△ABC绕定点P顺时针旋转得到的.如果用(2,1)表示方格纸上点A的位置,用(1,2)表示点B的位置,那么点P的位置为( )
A.(5,2) B.(2,5) C.(2,1) D.(1,2)
5.如图,将四边形ABOC绕点O顺时针旋转得到四边形DFOE,则下列角中不是旋转角的为( )
A.∠BOF B.∠AOD C.∠COE D.∠AOF
6.如图,一块含30°角的直角三角板ABC绕点C顺时针旋转一定角度得到△A'B'C,当B,C,A'在一条直线上时,三角板ABC的旋转角度为( )
A.150° B.120° C.60° D.30°
7.如图,边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB'C'D',则图中阴影部分的面积为( )
A. B. C.1- D.1-
8.如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB'C'的位置,使CC'∥AB,则旋转角的度数为( )
A.35° B.40° C.50° D.65°
二、填空题
9.如图,P为正方形ABCD内的一点,PC=1,将△CDP绕点C逆时针旋转得到△CBE,则PE= .
10.如图,在平面直角坐标系xOy中,点A,P分别在x轴、y轴上,∠APO=30°.先将线段PA沿y轴翻折得到线段PB,再将线段PA绕点P顺时针旋转30°得到线段PC,连接BC.若点A的坐标为(-1,0),则线段BC的长为 .
11.如图,在平面直角坐标系中,长方形OABC的顶点A,C分别在x轴,y轴上,点B在第一象限内,直线y=x+1交y轴于点D,且点D为CO的中点,将直线绕点D顺时针旋转15°经过点B,则点B的坐标为 .
12.如图3-2-13,将Rt△ABC的斜边AB绕点A顺时针旋转α(0°<α<90°)得到AE,直角边AC绕点A逆时针旋转β(0°<β<90°)得到AF,连接EF.若AB=3,AC=2,且α+β=∠B,则EF= .
三、解答题
13.如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,把△ABC绕点C逆时针旋转90°后得到△A1B1C.
(1)画出△A1B1C;
(2)求在旋转过程中,CA所扫过的面积.
14.如图,在等边三角形ABC中,点D是AB边上一点,连接CD,将线段CD绕点C按顺时针方向旋转60°后得到CE,连接AE.求证:AE∥BC.
15.如图,点O是等边三角形ABC内一点,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形
参考答案
1.C 2.C 3.A 4.A 5.D 6.A 7.C 8.C
9. 10. 2 11. (,2) 12.
13. (1)如图,△A1B1C为所求作的图形.
(2)∵AC===,∠ACA1=90°,
∴在旋转过程中,CA所扫过的面积为=×()2·π=.
14. ∵△ABC是等边三角形,
∴AC=BC,∠B=∠ACB=60°,
∵线段CD绕点C按顺时针方向旋转60°得到CE,
∴CD=CE,∠DCE=60°,
∴∠DCE=∠ACB,即∠BCD+∠DCA=∠DCA+∠ACE,
∴∠BCD=∠ACE,
在△BCD与△ACE中,
∴△BCD≌△ACE,
∴∠EAC=∠B=60°,
∴∠EAC=∠ACB,∴AE∥BC.
15. (1)证明:∵CO=CD,∠OCD=60°,
∴△COD是等边三角形.
(2)当α=150°,即∠BOC=150°时,△AOD是直角三角形.
理由:由旋转的性质得,△BOC≌△ADC,
∴∠ADC=∠BOC=150°,
又∵△COD是等边三角形,∴∠ODC=60°,
∴∠ADO=90°,即△AOD是直角三角形.
(3)①当AO=AD时,∠AOD=∠ADO.
∵∠AOD=360°-∠AOB-∠COD-α=360°-110°-60°-α=190°-α,∠ADO=
∠ADC-∠CDO=α-60°,
∴190°-α=α-60°,∴α=125°;
②当OA=OD时,∠OAD=∠ADO,
∵∠AOD=190°-α,∠ADO=α-60°,
∴∠OAD=180°-(∠AOD+∠ADO)=50°,
∴α-60°=50°,∴α=110°;
③当OD=AD时,∠OAD=∠AOD,
即190°-α=50°,∴α=140°.
综上所述,当α的度数为125°或110°或140°时,△AOD是等腰三角形.
一、选择题
1.下列物体的运动不是旋转的是( )
A.运转的摩天轮上的一只灯泡 B.正在走动的时针
C.骑自行车的人 D.正在转动的风车叶片
2.如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A'B'C,连接AB',若AB'=3,则∠A'的度数为( )
A.125° B.130° C.135° D.140°
3.若点A的坐标为(6,3),O为坐标原点,将OA绕点O按顺时针方向旋转90°得到OA',则点A'的坐标是( )
A.(3,-6) B.(-3,6) C.(-3,-6) D.(3,6)
4.如图,方格纸上的△DEF是由△ABC绕定点P顺时针旋转得到的.如果用(2,1)表示方格纸上点A的位置,用(1,2)表示点B的位置,那么点P的位置为( )
A.(5,2) B.(2,5) C.(2,1) D.(1,2)
5.如图,将四边形ABOC绕点O顺时针旋转得到四边形DFOE,则下列角中不是旋转角的为( )
A.∠BOF B.∠AOD C.∠COE D.∠AOF
6.如图,一块含30°角的直角三角板ABC绕点C顺时针旋转一定角度得到△A'B'C,当B,C,A'在一条直线上时,三角板ABC的旋转角度为( )
A.150° B.120° C.60° D.30°
7.如图,边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB'C'D',则图中阴影部分的面积为( )
A. B. C.1- D.1-
8.如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB'C'的位置,使CC'∥AB,则旋转角的度数为( )
A.35° B.40° C.50° D.65°
二、填空题
9.如图,P为正方形ABCD内的一点,PC=1,将△CDP绕点C逆时针旋转得到△CBE,则PE= .
10.如图,在平面直角坐标系xOy中,点A,P分别在x轴、y轴上,∠APO=30°.先将线段PA沿y轴翻折得到线段PB,再将线段PA绕点P顺时针旋转30°得到线段PC,连接BC.若点A的坐标为(-1,0),则线段BC的长为 .
11.如图,在平面直角坐标系中,长方形OABC的顶点A,C分别在x轴,y轴上,点B在第一象限内,直线y=x+1交y轴于点D,且点D为CO的中点,将直线绕点D顺时针旋转15°经过点B,则点B的坐标为 .
12.如图3-2-13,将Rt△ABC的斜边AB绕点A顺时针旋转α(0°<α<90°)得到AE,直角边AC绕点A逆时针旋转β(0°<β<90°)得到AF,连接EF.若AB=3,AC=2,且α+β=∠B,则EF= .
三、解答题
13.如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,把△ABC绕点C逆时针旋转90°后得到△A1B1C.
(1)画出△A1B1C;
(2)求在旋转过程中,CA所扫过的面积.
14.如图,在等边三角形ABC中,点D是AB边上一点,连接CD,将线段CD绕点C按顺时针方向旋转60°后得到CE,连接AE.求证:AE∥BC.
15.如图,点O是等边三角形ABC内一点,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形
参考答案
1.C 2.C 3.A 4.A 5.D 6.A 7.C 8.C
9. 10. 2 11. (,2) 12.
13. (1)如图,△A1B1C为所求作的图形.
(2)∵AC===,∠ACA1=90°,
∴在旋转过程中,CA所扫过的面积为=×()2·π=.
14. ∵△ABC是等边三角形,
∴AC=BC,∠B=∠ACB=60°,
∵线段CD绕点C按顺时针方向旋转60°得到CE,
∴CD=CE,∠DCE=60°,
∴∠DCE=∠ACB,即∠BCD+∠DCA=∠DCA+∠ACE,
∴∠BCD=∠ACE,
在△BCD与△ACE中,
∴△BCD≌△ACE,
∴∠EAC=∠B=60°,
∴∠EAC=∠ACB,∴AE∥BC.
15. (1)证明:∵CO=CD,∠OCD=60°,
∴△COD是等边三角形.
(2)当α=150°,即∠BOC=150°时,△AOD是直角三角形.
理由:由旋转的性质得,△BOC≌△ADC,
∴∠ADC=∠BOC=150°,
又∵△COD是等边三角形,∴∠ODC=60°,
∴∠ADO=90°,即△AOD是直角三角形.
(3)①当AO=AD时,∠AOD=∠ADO.
∵∠AOD=360°-∠AOB-∠COD-α=360°-110°-60°-α=190°-α,∠ADO=
∠ADC-∠CDO=α-60°,
∴190°-α=α-60°,∴α=125°;
②当OA=OD时,∠OAD=∠ADO,
∵∠AOD=190°-α,∠ADO=α-60°,
∴∠OAD=180°-(∠AOD+∠ADO)=50°,
∴α-60°=50°,∴α=110°;
③当OD=AD时,∠OAD=∠AOD,
即190°-α=50°,∴α=140°.
综上所述,当α的度数为125°或110°或140°时,△AOD是等腰三角形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
