2.3等差数列的前n项和 课件(共21张PPT)
文档属性
| 名称 | 2.3等差数列的前n项和 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 876.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-20 11:45:05 | ||
图片预览






文档简介
(共21张PPT)
等差数列的前n项和
——性质及其应用
1
复习旧知
2
情境导入
3
思考探究
4
归纳总结
5
应用练习
等差数列知识点梳理
基本概念 一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,这个数列就叫做等差数列。这个常数就叫做等差数列的公差(常用字母“d”表示)
基本公式 通项公式:an=a1+(n-1)d
项数n:n=(an-a1)/d+1
若a,A,b成等差数列,则等差中项A=(a+b)/2
性质 在等差数列{an}中,a1+an=a2+an-1=a3+an-2+......
1
复习旧知
3
思考探究
4
归纳总结
5
应用练习
2
情境导入
泰姬陵坐落于印度古都阿格,是17世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建,它宏伟壮观,纯白大理石砌建而成的主体建筑叫人心醉神迷,成为世界七大奇迹之一。陵寝以宝石镶嵌,图案之细致令人叫绝。传说陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有21层,奢靡之程度,可见一斑。你知道这个图案一共花了多少宝石吗
思考
1
复习旧知
2
情境导入
3
思考探究
4
归纳总结
5
应用练习
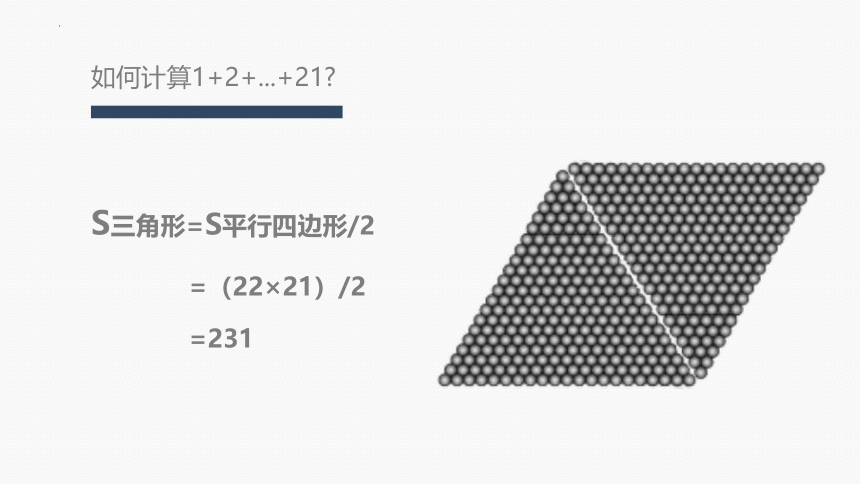
如何计算1+2+...+21
如何计算1+2+...+21
如何计算1+2+...+21
S三角形=S平行四边形/2
=(22×21)/2
=231
这是大家小学时就知道的一个故事,高斯的算法非常高明,回忆一下他是怎样算的
请输入文本内容
请输入文本内容
请输入文本内容
请输入文本内容
请输入文本内容
如何计算1+2+...+100
高斯算法的高明之处在于他发现这100个数可以分为50组,第一个数与最后一个数一组,第二个数与倒数第二个数一组,第三个数与倒数第三个数一组,...,每组数的和均都等于101,50个101就等于5050了。高斯算法将加法问题转化为乘法运算,迅速准确得到了
结果.
如何计算1+2+...+100
高斯算法的高明之处在于他发现这100个数可以分为50组,第一个数与最后一个数一组,第二个数与倒数第二个数一组,第三个数与倒数第三个数一组,...,每组数的和均都等于101,50个101就等于5050了。高斯算法将加法问题转化为乘法运算,迅速准确得到了
结果.
如何计算1+2+...+100
有哪些不足呢?
问题:设等差数列{an }的首项为a1,公差为d,尝试推导计算等差数列的前n项和Sn=a1+a2+...+an
请输入文本内容
请输入文本内容
请输入文本内容
请输入文本内容
请输入文本内容
小组讨论
等差数列{an}的前n项和Sn满足:
请输入文本内容
请输入文本内容
请输入文本内容
请输入文本内容
请输入文本内容
推导过程
Sn=a1+a2+...+an-1+an
Sn=an+an-1+...+a2+a1
2Sn=(a1+an)+(a2+an-1)+...
又a1+an=a2+an-1=a3+an-2+...
Sn=n×(a1+an)/2=na1+n(n+1)/2
1
复习旧知
2
情境导入
3
思考探究
4
归纳总结
5
应用练习
等差数列知识点梳理
基本概念 一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,这个数列就叫做等差数列。这个常数就叫做等差数列的公差(常用字母“d”表示)
基本公式 通项公式:an=a1+(n-1)d
项数n:n=(an-a1)/d+1
若a,A,b成等差数列,则等差中项A=(a+b)/2
前n项和公式:Sn=n×(a1+an)/2=na1+n(n+1)/2
性质 在等差数列{an}中,a1+an=a2+an-1=a3+an-2+......
1
复习旧知
2
情境导入
3
思考探究
4
归纳总结
5
应用练习
计算:
(1)1+2+3+...+n
(2) 1+3+5+...+(2n-1)
(3) 2+4+6+...+2n
(4) 1-2+3-4+5-6+... +(2n-1)-2n
例1
何老师按揭买房,向银行贷款25万元,采取等额本金的还款方式,即每月还款额比上月减少一定的数额。2007 年1月,我第一次向银行还款2348元,以后每月比上月的还款额减少5元,若以2007年1月银行贷款利率为基准利率,那么到2026年12月最后一次还款为止,何老师连本带利一共还款多少万元
例2
(一)阅读作业:通读教材,复习巩固,思考等差数列的通项公式的求法;
(二)教材书后习题;
(三)拓展选做题:模仿等差数列的定义,思考有没有“等和数列”。如果有,请探究它的定义、通项公式和相关的性质。
作业
THANKS!
等差数列的前n项和
——性质及其应用
1
复习旧知
2
情境导入
3
思考探究
4
归纳总结
5
应用练习
等差数列知识点梳理
基本概念 一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,这个数列就叫做等差数列。这个常数就叫做等差数列的公差(常用字母“d”表示)
基本公式 通项公式:an=a1+(n-1)d
项数n:n=(an-a1)/d+1
若a,A,b成等差数列,则等差中项A=(a+b)/2
性质 在等差数列{an}中,a1+an=a2+an-1=a3+an-2+......
1
复习旧知
3
思考探究
4
归纳总结
5
应用练习
2
情境导入
泰姬陵坐落于印度古都阿格,是17世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建,它宏伟壮观,纯白大理石砌建而成的主体建筑叫人心醉神迷,成为世界七大奇迹之一。陵寝以宝石镶嵌,图案之细致令人叫绝。传说陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有21层,奢靡之程度,可见一斑。你知道这个图案一共花了多少宝石吗
思考
1
复习旧知
2
情境导入
3
思考探究
4
归纳总结
5
应用练习
如何计算1+2+...+21
如何计算1+2+...+21
如何计算1+2+...+21
S三角形=S平行四边形/2
=(22×21)/2
=231
这是大家小学时就知道的一个故事,高斯的算法非常高明,回忆一下他是怎样算的
请输入文本内容
请输入文本内容
请输入文本内容
请输入文本内容
请输入文本内容
如何计算1+2+...+100
高斯算法的高明之处在于他发现这100个数可以分为50组,第一个数与最后一个数一组,第二个数与倒数第二个数一组,第三个数与倒数第三个数一组,...,每组数的和均都等于101,50个101就等于5050了。高斯算法将加法问题转化为乘法运算,迅速准确得到了
结果.
如何计算1+2+...+100
高斯算法的高明之处在于他发现这100个数可以分为50组,第一个数与最后一个数一组,第二个数与倒数第二个数一组,第三个数与倒数第三个数一组,...,每组数的和均都等于101,50个101就等于5050了。高斯算法将加法问题转化为乘法运算,迅速准确得到了
结果.
如何计算1+2+...+100
有哪些不足呢?
问题:设等差数列{an }的首项为a1,公差为d,尝试推导计算等差数列的前n项和Sn=a1+a2+...+an
请输入文本内容
请输入文本内容
请输入文本内容
请输入文本内容
请输入文本内容
小组讨论
等差数列{an}的前n项和Sn满足:
请输入文本内容
请输入文本内容
请输入文本内容
请输入文本内容
请输入文本内容
推导过程
Sn=a1+a2+...+an-1+an
Sn=an+an-1+...+a2+a1
2Sn=(a1+an)+(a2+an-1)+...
又a1+an=a2+an-1=a3+an-2+...
Sn=n×(a1+an)/2=na1+n(n+1)/2
1
复习旧知
2
情境导入
3
思考探究
4
归纳总结
5
应用练习
等差数列知识点梳理
基本概念 一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,这个数列就叫做等差数列。这个常数就叫做等差数列的公差(常用字母“d”表示)
基本公式 通项公式:an=a1+(n-1)d
项数n:n=(an-a1)/d+1
若a,A,b成等差数列,则等差中项A=(a+b)/2
前n项和公式:Sn=n×(a1+an)/2=na1+n(n+1)/2
性质 在等差数列{an}中,a1+an=a2+an-1=a3+an-2+......
1
复习旧知
2
情境导入
3
思考探究
4
归纳总结
5
应用练习
计算:
(1)1+2+3+...+n
(2) 1+3+5+...+(2n-1)
(3) 2+4+6+...+2n
(4) 1-2+3-4+5-6+... +(2n-1)-2n
例1
何老师按揭买房,向银行贷款25万元,采取等额本金的还款方式,即每月还款额比上月减少一定的数额。2007 年1月,我第一次向银行还款2348元,以后每月比上月的还款额减少5元,若以2007年1月银行贷款利率为基准利率,那么到2026年12月最后一次还款为止,何老师连本带利一共还款多少万元
例2
(一)阅读作业:通读教材,复习巩固,思考等差数列的通项公式的求法;
(二)教材书后习题;
(三)拓展选做题:模仿等差数列的定义,思考有没有“等和数列”。如果有,请探究它的定义、通项公式和相关的性质。
作业
THANKS!
