人教版四年级数学上册 第四单元第3课时《积的变化规律》精品教学方案
文档属性
| 名称 | 人教版四年级数学上册 第四单元第3课时《积的变化规律》精品教学方案 | 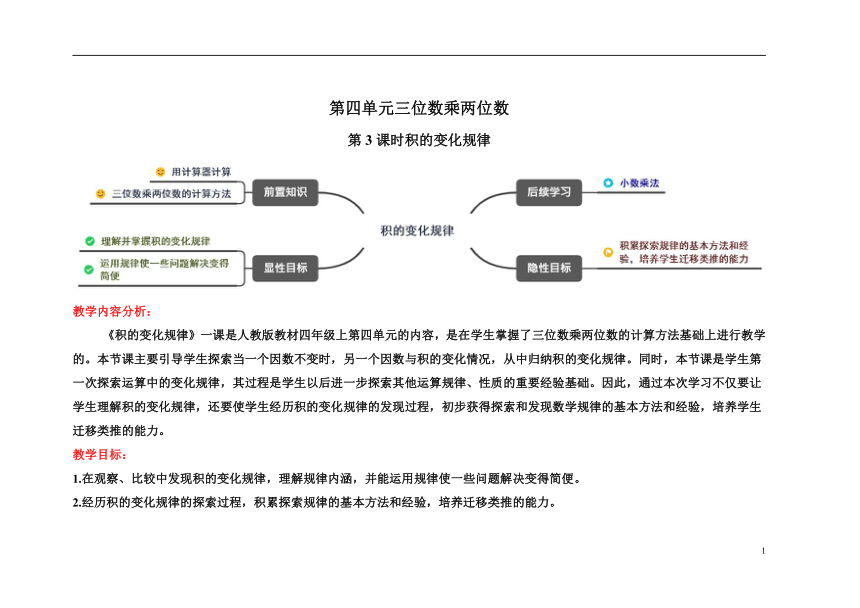 | |
| 格式 | docx | ||
| 文件大小 | 141.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-20 14:22:50 | ||
图片预览



文档简介
第四单元三位数乘两位数
第3课时积的变化规律
教学内容分析:
《积的变化规律》一课是人教版教材四年级上第四单元的内容,是在学生掌握了三位数乘两位数的计算方法基础上进行教学的。本节课主要引导学生探索当一个因数不变时,另一个因数与积的变化情况,从中归纳积的变化规律。同时,本节课是学生第一次探索运算中的变化规律,其过程是学生以后进一步探索其他运算规律、性质的重要经验基础。因此,通过本次学习不仅要让学生理解积的变化规律,还要使学生经历积的变化规律的发现过程,初步获得探索和发现数学规律的基本方法和经验,培养学生迁移类推的能力。
教学目标:
1.在观察、比较中发现积的变化规律,理解规律内涵,并能运用规律使一些问题解决变得简便。
2.经历积的变化规律的探索过程,积累探索规律的基本方法和经验,培养迁移类推的能力。
教学重点:
经历探索规律的过程,发现并理解积的变化规律。
教学难点:
能运用规律使一些问题解决变得简便。
教学过程:
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 1.课件出示下题,比一比谁算得快。 学生独立完成 由计算比赛引入,将学生的学习兴趣充分调动起来。
2.校对口算,学生介绍方法。 问题:你们做得又快又对,是怎么算的? 学生校对答案 回答问题: 生1:第1题和第2题用口算计算,第3题用笔算计算。 生2:因数从2到4乘2,积应当乘2,是100;因数从4到12乘3,积也应当乘3,是300。 将书中的例题进行调整,改变了以往以简单的因数添“0”作为教学研究的素材,而采用 “25×12”这样需要笔算的材料,通过让学生介绍各自的计算方法,使学生初步感悟到“一个因数不变,另一个因数变了,积也变了”,从而获得一定的感性认识,为该堂新知识点的学习作好铺垫。
环节二 探究新知 1.自主探索: “一个因数不变,另一个因数乘几,积也乘相同的数”的规律。 课件呈现算式: 问题1:仔细观察这组算式,你有什么发现? 要求:(1)写一写,画一画,将你的发现在算式上表示出来。(2)同桌交流,说一说你的发现。 问题2:除了这些算式外,还有哪两个算式也有这样的规律? 问题3:谁能把刚才发现的规律用一句话来概括? 小结:两数相乘,一个因数不变,另一个因数乘几,积也乘相同的数。 回答问题: 生1:一个因数不变,另一个因数不同,积也不同。 生2:第2个算式与第1个算式相比,一个因数不变,另一个因数乘2,积也乘2。 生3;第3个算式与第2个算式相比,一个因数不变,另一个因数乘3,积也乘3。 回答问题: 生:第3个算式与第1个算式相比,一个因数不变,另一个因数乘6,积也乘6. 回答问题: 生1:一个因数不变,另一个因数变大,积也变大。 生2:一个因数不变,另一个因数乘几,积也乘相同的数。 本环节教师引导学生借助口算素材自主探究,让学生充分经历探索过程,积累规律探索的经验,提升学生的探究能力。
2.迁移学习:“一个因数不变,另一个因数除以几(0除外),积也除以相同的数”的规律。 课件呈现算式: 要求:①想一想,如何能做得又快又对。②完成后自己校对答案,同桌交流计算方法。 问题1:如何能算得又快又对,谁发现了其中的规律? : 问题2:你能把这个规律概括成一句话吗? 问题3:可以除以任何数吗? 小结:一个因数不变,另一个因数除以几(0除外),积也除以相同的数。 学生尝试自己解决后校对答案 回答问题: 生:第2个算式与第1个算式相比,一个因数不变,另一个因数除以3,积也要除以3;第3个算式与第2个算式相比,一个因数不变,另一个因数除以4,积也要除以4。 回答问题: 生:一个因数不变,另一个因数除以几,积也要除以相同的数。 回答问题: 生:不是,0除外,因为0不能做除数。 回答问题: 生:一个因数不变,另一个因数乘几或除以几(0除外),积也乘(或除以)相同的数。 本环节给了学生更加广阔的思维空间。前面研究积随因数扩大而扩大的规律时,学生已经积累探索规律的经验,再研究积随因数缩小而缩小的规律时,老师放手让学生用刚才掌握的研究方法去解决问题,进而实现方法的迁移运用。
3.验证规律。 (1)先用积的变化规律填空,再用笔算或计算器验算。 (2)请自己举例两组算式,一组3个,展现积分别随一个因数扩大、缩小的变化情况。 问题:谁能把我们刚才发现的两个规律合一句话? 按要求验证规律。 回答问题: 生:一个因数不变,另一个因数乘几或除以几(0除外),积也乘(或除以)相同的数。 让学生经历验证积的变化规律的过程,可以加深学生对规律的理解,进而能更好地掌握规律。
环节三 巩固新知 练习1: 根据第一个算式的结果,写出下面算式的积 125×8=1000 64×25=1600 125×16= 32×25= 125×96= 16×25 = 问题:说一说你是怎么想的? 学生独立完成后校对答案并说理 此练习的目的是巩固刚刚所寻找到的“积的变化规律”,也能检查学生对最基本的知识掌握的情况。
练习2: 扩大后的绿地面积是多少? 数形结合沟通联系积的变化规律 问题1:谁能看明白第2种方法? 问题2:如果长不变,宽乘4、乘5……,面积怎么变? 问题3:如果宽不变,长除以2、除以3……,面积怎么变? 小结:长乘宽等于长方形的面积,长或宽的变化,引起面积的变化,和积的变化规律是一样的。 学生解答: 方法1: 200÷8×24=600(平方米) 方法2: 24÷8×200=600(平方米) 回答问题: 生:长方形的长不变,宽从8米到24米乘了3,面积也要乘3。(学生回答教师课件演示) 回答问题:长不变,宽乘几,面积也乘几。(教师课件演示) 回答问题:宽不变,长除以几,面积也除以几。(教师课件演示) 一方面是把刚学到的“积的变化规律”引导学生加以运用,感受规律的优越性,激发学生运用规律的意识;另一方面利用数与形结合起来,把静态的数与数之间的关系转变成为了动态的变化过程。借助于“形”的变化深化对积的变化规律的认识
练习3: 在○里填运算符号,在□里填上数,你有什么发现。 10×30=300 (10○□)×(30○□)= 小结引申规律:①一个因数乘一个数,另一个因数乘另一个数,积就乘这两个数的积。 ②一个因数除以一个数(0除外),另一个因数除以另一个数(0除外),积就除以这两个数的积。 ③一个因数乘(或除以)一个数(0除外),另一个因数同时除以(或乘)相同的数,它们的积不变。 独立思考,学生列举 生1:(10×2) ×(30×3)=300×(2×3) 生2:(10×3)×(30÷3)=300 生3:(10÷2)×(30÷3)=300÷(2×3) 本环节为学生创设了充分的思考空间,引导学生探究当两个因数都发生变化时积是如何变化的,充分调动学生去开动脑筋,大胆把猜想融入到课本内容中,有了此环节,整个内容就变得完整,更重要的是帮助学生建立拓展延伸、探究问题的意识。
环节四 课堂小结 这节课我们学习了什么? 如果再往后学你有什么新问题? 回顾本节课自己的体会和收获并提出新的问题。 鼓励学生畅谈自己的收获和体会,有哪些认知上的冲突,遇到问题是如何解决的。
环节五 布置作业 教材P54第1题,P55第10题
1
第3课时积的变化规律
教学内容分析:
《积的变化规律》一课是人教版教材四年级上第四单元的内容,是在学生掌握了三位数乘两位数的计算方法基础上进行教学的。本节课主要引导学生探索当一个因数不变时,另一个因数与积的变化情况,从中归纳积的变化规律。同时,本节课是学生第一次探索运算中的变化规律,其过程是学生以后进一步探索其他运算规律、性质的重要经验基础。因此,通过本次学习不仅要让学生理解积的变化规律,还要使学生经历积的变化规律的发现过程,初步获得探索和发现数学规律的基本方法和经验,培养学生迁移类推的能力。
教学目标:
1.在观察、比较中发现积的变化规律,理解规律内涵,并能运用规律使一些问题解决变得简便。
2.经历积的变化规律的探索过程,积累探索规律的基本方法和经验,培养迁移类推的能力。
教学重点:
经历探索规律的过程,发现并理解积的变化规律。
教学难点:
能运用规律使一些问题解决变得简便。
教学过程:
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 1.课件出示下题,比一比谁算得快。 学生独立完成 由计算比赛引入,将学生的学习兴趣充分调动起来。
2.校对口算,学生介绍方法。 问题:你们做得又快又对,是怎么算的? 学生校对答案 回答问题: 生1:第1题和第2题用口算计算,第3题用笔算计算。 生2:因数从2到4乘2,积应当乘2,是100;因数从4到12乘3,积也应当乘3,是300。 将书中的例题进行调整,改变了以往以简单的因数添“0”作为教学研究的素材,而采用 “25×12”这样需要笔算的材料,通过让学生介绍各自的计算方法,使学生初步感悟到“一个因数不变,另一个因数变了,积也变了”,从而获得一定的感性认识,为该堂新知识点的学习作好铺垫。
环节二 探究新知 1.自主探索: “一个因数不变,另一个因数乘几,积也乘相同的数”的规律。 课件呈现算式: 问题1:仔细观察这组算式,你有什么发现? 要求:(1)写一写,画一画,将你的发现在算式上表示出来。(2)同桌交流,说一说你的发现。 问题2:除了这些算式外,还有哪两个算式也有这样的规律? 问题3:谁能把刚才发现的规律用一句话来概括? 小结:两数相乘,一个因数不变,另一个因数乘几,积也乘相同的数。 回答问题: 生1:一个因数不变,另一个因数不同,积也不同。 生2:第2个算式与第1个算式相比,一个因数不变,另一个因数乘2,积也乘2。 生3;第3个算式与第2个算式相比,一个因数不变,另一个因数乘3,积也乘3。 回答问题: 生:第3个算式与第1个算式相比,一个因数不变,另一个因数乘6,积也乘6. 回答问题: 生1:一个因数不变,另一个因数变大,积也变大。 生2:一个因数不变,另一个因数乘几,积也乘相同的数。 本环节教师引导学生借助口算素材自主探究,让学生充分经历探索过程,积累规律探索的经验,提升学生的探究能力。
2.迁移学习:“一个因数不变,另一个因数除以几(0除外),积也除以相同的数”的规律。 课件呈现算式: 要求:①想一想,如何能做得又快又对。②完成后自己校对答案,同桌交流计算方法。 问题1:如何能算得又快又对,谁发现了其中的规律? : 问题2:你能把这个规律概括成一句话吗? 问题3:可以除以任何数吗? 小结:一个因数不变,另一个因数除以几(0除外),积也除以相同的数。 学生尝试自己解决后校对答案 回答问题: 生:第2个算式与第1个算式相比,一个因数不变,另一个因数除以3,积也要除以3;第3个算式与第2个算式相比,一个因数不变,另一个因数除以4,积也要除以4。 回答问题: 生:一个因数不变,另一个因数除以几,积也要除以相同的数。 回答问题: 生:不是,0除外,因为0不能做除数。 回答问题: 生:一个因数不变,另一个因数乘几或除以几(0除外),积也乘(或除以)相同的数。 本环节给了学生更加广阔的思维空间。前面研究积随因数扩大而扩大的规律时,学生已经积累探索规律的经验,再研究积随因数缩小而缩小的规律时,老师放手让学生用刚才掌握的研究方法去解决问题,进而实现方法的迁移运用。
3.验证规律。 (1)先用积的变化规律填空,再用笔算或计算器验算。 (2)请自己举例两组算式,一组3个,展现积分别随一个因数扩大、缩小的变化情况。 问题:谁能把我们刚才发现的两个规律合一句话? 按要求验证规律。 回答问题: 生:一个因数不变,另一个因数乘几或除以几(0除外),积也乘(或除以)相同的数。 让学生经历验证积的变化规律的过程,可以加深学生对规律的理解,进而能更好地掌握规律。
环节三 巩固新知 练习1: 根据第一个算式的结果,写出下面算式的积 125×8=1000 64×25=1600 125×16= 32×25= 125×96= 16×25 = 问题:说一说你是怎么想的? 学生独立完成后校对答案并说理 此练习的目的是巩固刚刚所寻找到的“积的变化规律”,也能检查学生对最基本的知识掌握的情况。
练习2: 扩大后的绿地面积是多少? 数形结合沟通联系积的变化规律 问题1:谁能看明白第2种方法? 问题2:如果长不变,宽乘4、乘5……,面积怎么变? 问题3:如果宽不变,长除以2、除以3……,面积怎么变? 小结:长乘宽等于长方形的面积,长或宽的变化,引起面积的变化,和积的变化规律是一样的。 学生解答: 方法1: 200÷8×24=600(平方米) 方法2: 24÷8×200=600(平方米) 回答问题: 生:长方形的长不变,宽从8米到24米乘了3,面积也要乘3。(学生回答教师课件演示) 回答问题:长不变,宽乘几,面积也乘几。(教师课件演示) 回答问题:宽不变,长除以几,面积也除以几。(教师课件演示) 一方面是把刚学到的“积的变化规律”引导学生加以运用,感受规律的优越性,激发学生运用规律的意识;另一方面利用数与形结合起来,把静态的数与数之间的关系转变成为了动态的变化过程。借助于“形”的变化深化对积的变化规律的认识
练习3: 在○里填运算符号,在□里填上数,你有什么发现。 10×30=300 (10○□)×(30○□)= 小结引申规律:①一个因数乘一个数,另一个因数乘另一个数,积就乘这两个数的积。 ②一个因数除以一个数(0除外),另一个因数除以另一个数(0除外),积就除以这两个数的积。 ③一个因数乘(或除以)一个数(0除外),另一个因数同时除以(或乘)相同的数,它们的积不变。 独立思考,学生列举 生1:(10×2) ×(30×3)=300×(2×3) 生2:(10×3)×(30÷3)=300 生3:(10÷2)×(30÷3)=300÷(2×3) 本环节为学生创设了充分的思考空间,引导学生探究当两个因数都发生变化时积是如何变化的,充分调动学生去开动脑筋,大胆把猜想融入到课本内容中,有了此环节,整个内容就变得完整,更重要的是帮助学生建立拓展延伸、探究问题的意识。
环节四 课堂小结 这节课我们学习了什么? 如果再往后学你有什么新问题? 回顾本节课自己的体会和收获并提出新的问题。 鼓励学生畅谈自己的收获和体会,有哪些认知上的冲突,遇到问题是如何解决的。
环节五 布置作业 教材P54第1题,P55第10题
1
