人教版四年级数学上册 第四单元第4课时单价、数量和总价表格式精品教学方案
文档属性
| 名称 | 人教版四年级数学上册 第四单元第4课时单价、数量和总价表格式精品教学方案 | 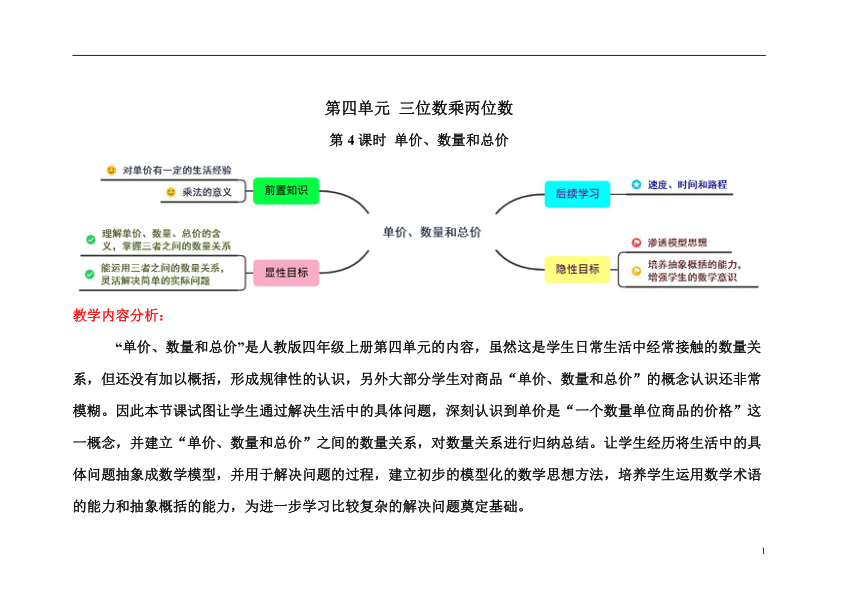 | |
| 格式 | docx | ||
| 文件大小 | 101.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-20 14:22:43 | ||
图片预览


文档简介
第四单元 三位数乘两位数
第4课时 单价、数量和总价
教学内容分析:
“单价、数量和总价”是人教版四年级上册第四单元的内容,虽然这是学生日常生活中经常接触的数量关系,但还没有加以概括,形成规律性的认识,另外大部分学生对商品“单价、数量和总价”的概念认识还非常模糊。因此本节课试图让学生通过解决生活中的具体问题,深刻认识到单价是“一个数量单位商品的价格”这一概念,并建立“单价、数量和总价”之间的数量关系,对数量关系进行归纳总结。让学生经历将生活中的具体问题抽象成数学模型,并用于解决问题的过程,建立初步的模型化的数学思想方法,培养学生运用数学术语的能力和抽象概括的能力,为进一步学习比较复杂的解决问题奠定基础。
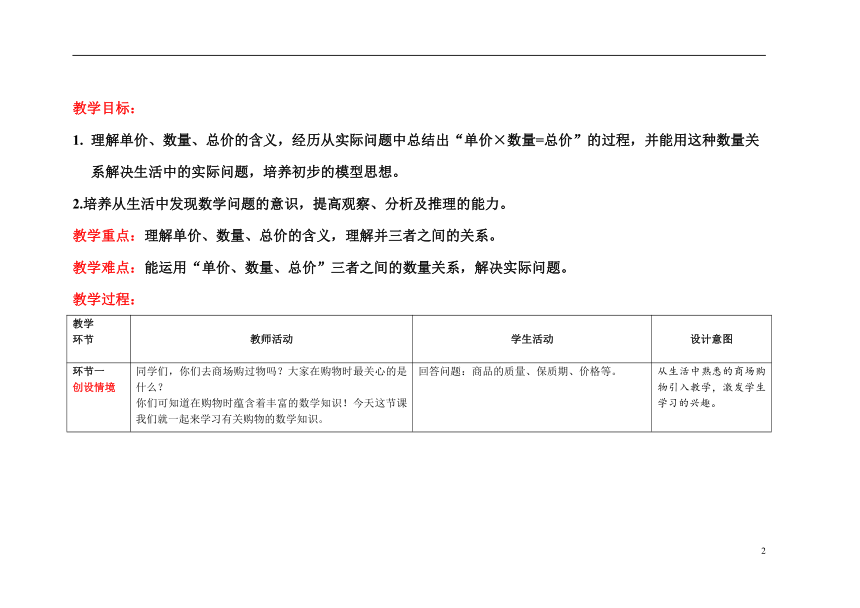
教学目标:
理解单价、数量、总价的含义,经历从实际问题中总结出“单价×数量=总价”的过程,并能用这种数量关系解决生活中的实际问题,培养初步的模型思想。
2.培养从生活中发现数学问题的意识,提高观察、分析及推理的能力。
教学重点:理解单价、数量、总价的含义,理解并三者之间的关系。
教学难点:能运用“单价、数量、总价”三者之间的数量关系,解决实际问题。
教学过程:
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 同学们,你们去商场购过物吗?大家在购物时最关心的是什么? 你们可知道在购物时蕴含着丰富的数学知识!今天这节课我们就一起来学习有关购物的数学知识。 回答问题:商品的质量、保质期、价格等。 从生活中熟悉的商场购物引入教学,激发学生学习的兴趣。
环节二 探究新知 1.认识单价、数量和总价的含义。 出示例4(1)(2)问题并提问: (1)篮球每个80元,买3个要多少钱? (2)鱼每千克10元,买4千克要多少钱? 出示算式:80×3=240(元) 10×4=40(元) 问题1:算式中的每一部分表示的意义是什么?: 问题2:这两个问题中的数学信息有什么共同点? 明确:像这样,“每个篮球的价钱”、“每千克鱼的价钱”都是指每件商品的价钱,叫做单价,这里的80元和10元就是单价;买了多少,叫做数量,3个和4千克都是数量;一共用的钱,叫做总价。 出示:找一找,信息中这些购物问题中的单价、数量与总价。 一个文具盒8元,买4个需要32元。 妈妈买了7米窗帘布,每米窗帘布35元,一共花了245元。 每千克香蕉7元,56元可以买8千克香蕉。 2.探究单价、数量和总价之间的关系 问题1:从上面的例子中,你们发现单价、数量与总价之间有什么关系?请用数据进行举例说明。 问题2:单价、数量和总价三个数量之中,已知单价和数量,可以求出总价。那么,已知其他两个量,怎样求出第三个量? 学生独立思考并回答:买3个篮球要80×3=240(元);买4千克鱼要10×4=40(元)。 学生回答: 生1:80×3=240(元)。80是一个篮球的价钱,3是要买的个数,80×3是3个80元,240元就是买3个篮球的总钱数。 生2:10×4=40(元)。10元是一千克鱼的价钱,4是要买的千克数,10×4是4个40元,40元就是买4千克鱼的总钱数。 学生回答: 生1:都是购物问题。 生2:都是已知每个商品或每千克商品的价钱和买了多少,求一共的钱数。 学生独立思考后回答问题。 生1:一个文具盒8元是单价,买4个是数量,32元是总价。 生2:每米窗帘布35元是单价,7米是数量,245元是总价。 生3:每千克香蕉7元是单价,8千克是数量,56元是总价。 学生回答: 生1:一个文具盒8元,买4个就需要4个8元,共32元,这里8元对应单价,4个对应数量,32对应总价。 单价 × 数量 = 总价 8 × 4 = 32 生2:每米窗帘布35元,买7米就需要7个35元,共245元,这里的35元对应单价,7米对应数量,245元对应总价。 单价 × 数量 = 总价 35 × 7 = 245元 生3:每千克香蕉7元,买8千克就需要8个7元,共56元,这里的7元对应单价,8千克对应数量,56元对应总价。 单价 × 数量 = 总价 7 × 8 = 56元 学生回答: 生1:已知单价和总价,求数量:总价÷单价=数量。 生2:已知数量和总价,求单价:总价÷数量=单价。 一方面,教师提出“想一想算式每一部分表示的意义是什么?”能够引导学生形成单价、数量和总价的表象。另一方面,通过独立解决做篮球和鱼的总价,为理解单价、数量和总价的含义做好了铺垫。 利用练习加深学生对单价、数量和总价的理解,有利于为探究单价、数量和总价之间的关系建立模型。 在学生明确了三者的含义之后,引导学生从中发现三者之间存在的数量关系:单价×数量=总价。并且根据这个数量关系推导出另外两个数量关系。
环节三 巩固练习 练习1:选一选 。 (1)用“单价×数量=总价”来解决的有( ) A.足球每个40元,买6个共要多少钱? B.玩5次过山车,每次15元,要多少钱? C.一碗面10元,100元可以买几碗这样的面? 问题1:为什么选A和B说说你的理由,C选项为什么不行? (2)用“总价÷数量=单价”解决的有( ) A.买5支笔用去10元,每支笔多少元? B.有48块糖,每袋装8块,可以装几袋? C.买9本同样的笔记本花了45元,每本笔记本多少钱? 问题2:为什么不选B,B也是用除法来解决的? 练习2:把相关数据填在相应的格子里。 (1)一千克猪肉18元,买5千克猪肉用去90元。 (2)每公顷工业用地售价10万元,买5公顷需要50万元。 (3)一箱可乐12瓶,每箱24元,每瓶2元,买了3箱共付72元。 讨论:这里的24元,为什么一会儿是单价,一会儿 是总价? 小结:任何一个条件在不同的问题情境中所表示数量的意义是可以变化的。 独立完成,校对 学生回答: 生1:足球每个40元是单价,6个是数量,要求共要多少钱是总价,所以可以用单价×数量=总价来解决。 生2:每次15元是单价,5次是数量,要多少钱是总价,所以也可以用单价×数量=总价来解决。 生3:一碗面10元是单价,100元是总价,要解决可以买几碗这样的面,要用总价÷单价=数量来解决。 学生回答: 生:A选项中的10元是总价,5支是数量,用总价÷数量=单价,能解决问题。C选项中45元是总价,9本是数量,用总价÷数量=单价也能解决问题,虽然B选项虽然能用除法解决,但48块不是总价,所以不符合这种数量关系。 学生独立填表 学生回答:每箱可乐24元,对于一瓶一瓶来说,它就是12瓶的总价;而对于3箱来说,这时24就是单价。 在初步获得总价模型的基础上,帮助学生掌握不同情境中单价、数量和总价的含义,并通过解决问题,培养灵活辨识数量关系的能力。 根据信息,结合三者数量关系,选择数据填表格,一方面促进学生解决问题能力的提升,另一方面,通过第三小题的辨析讨论让学生感受单价与总价的相对性,同时也能让学生体会解决问题时审题的重要性。
环节四 课堂小结 你有什么收获? 回顾本节课自己的体会和收获。 鼓励学生畅谈自己的收获和体会,加深对所学知识的理解和掌握。
环节六 布置作业 教材P52页做一做第2题,教材54页练习九第3题
1
第4课时 单价、数量和总价
教学内容分析:
“单价、数量和总价”是人教版四年级上册第四单元的内容,虽然这是学生日常生活中经常接触的数量关系,但还没有加以概括,形成规律性的认识,另外大部分学生对商品“单价、数量和总价”的概念认识还非常模糊。因此本节课试图让学生通过解决生活中的具体问题,深刻认识到单价是“一个数量单位商品的价格”这一概念,并建立“单价、数量和总价”之间的数量关系,对数量关系进行归纳总结。让学生经历将生活中的具体问题抽象成数学模型,并用于解决问题的过程,建立初步的模型化的数学思想方法,培养学生运用数学术语的能力和抽象概括的能力,为进一步学习比较复杂的解决问题奠定基础。
教学目标:
理解单价、数量、总价的含义,经历从实际问题中总结出“单价×数量=总价”的过程,并能用这种数量关系解决生活中的实际问题,培养初步的模型思想。
2.培养从生活中发现数学问题的意识,提高观察、分析及推理的能力。
教学重点:理解单价、数量、总价的含义,理解并三者之间的关系。
教学难点:能运用“单价、数量、总价”三者之间的数量关系,解决实际问题。
教学过程:
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 同学们,你们去商场购过物吗?大家在购物时最关心的是什么? 你们可知道在购物时蕴含着丰富的数学知识!今天这节课我们就一起来学习有关购物的数学知识。 回答问题:商品的质量、保质期、价格等。 从生活中熟悉的商场购物引入教学,激发学生学习的兴趣。
环节二 探究新知 1.认识单价、数量和总价的含义。 出示例4(1)(2)问题并提问: (1)篮球每个80元,买3个要多少钱? (2)鱼每千克10元,买4千克要多少钱? 出示算式:80×3=240(元) 10×4=40(元) 问题1:算式中的每一部分表示的意义是什么?: 问题2:这两个问题中的数学信息有什么共同点? 明确:像这样,“每个篮球的价钱”、“每千克鱼的价钱”都是指每件商品的价钱,叫做单价,这里的80元和10元就是单价;买了多少,叫做数量,3个和4千克都是数量;一共用的钱,叫做总价。 出示:找一找,信息中这些购物问题中的单价、数量与总价。 一个文具盒8元,买4个需要32元。 妈妈买了7米窗帘布,每米窗帘布35元,一共花了245元。 每千克香蕉7元,56元可以买8千克香蕉。 2.探究单价、数量和总价之间的关系 问题1:从上面的例子中,你们发现单价、数量与总价之间有什么关系?请用数据进行举例说明。 问题2:单价、数量和总价三个数量之中,已知单价和数量,可以求出总价。那么,已知其他两个量,怎样求出第三个量? 学生独立思考并回答:买3个篮球要80×3=240(元);买4千克鱼要10×4=40(元)。 学生回答: 生1:80×3=240(元)。80是一个篮球的价钱,3是要买的个数,80×3是3个80元,240元就是买3个篮球的总钱数。 生2:10×4=40(元)。10元是一千克鱼的价钱,4是要买的千克数,10×4是4个40元,40元就是买4千克鱼的总钱数。 学生回答: 生1:都是购物问题。 生2:都是已知每个商品或每千克商品的价钱和买了多少,求一共的钱数。 学生独立思考后回答问题。 生1:一个文具盒8元是单价,买4个是数量,32元是总价。 生2:每米窗帘布35元是单价,7米是数量,245元是总价。 生3:每千克香蕉7元是单价,8千克是数量,56元是总价。 学生回答: 生1:一个文具盒8元,买4个就需要4个8元,共32元,这里8元对应单价,4个对应数量,32对应总价。 单价 × 数量 = 总价 8 × 4 = 32 生2:每米窗帘布35元,买7米就需要7个35元,共245元,这里的35元对应单价,7米对应数量,245元对应总价。 单价 × 数量 = 总价 35 × 7 = 245元 生3:每千克香蕉7元,买8千克就需要8个7元,共56元,这里的7元对应单价,8千克对应数量,56元对应总价。 单价 × 数量 = 总价 7 × 8 = 56元 学生回答: 生1:已知单价和总价,求数量:总价÷单价=数量。 生2:已知数量和总价,求单价:总价÷数量=单价。 一方面,教师提出“想一想算式每一部分表示的意义是什么?”能够引导学生形成单价、数量和总价的表象。另一方面,通过独立解决做篮球和鱼的总价,为理解单价、数量和总价的含义做好了铺垫。 利用练习加深学生对单价、数量和总价的理解,有利于为探究单价、数量和总价之间的关系建立模型。 在学生明确了三者的含义之后,引导学生从中发现三者之间存在的数量关系:单价×数量=总价。并且根据这个数量关系推导出另外两个数量关系。
环节三 巩固练习 练习1:选一选 。 (1)用“单价×数量=总价”来解决的有( ) A.足球每个40元,买6个共要多少钱? B.玩5次过山车,每次15元,要多少钱? C.一碗面10元,100元可以买几碗这样的面? 问题1:为什么选A和B说说你的理由,C选项为什么不行? (2)用“总价÷数量=单价”解决的有( ) A.买5支笔用去10元,每支笔多少元? B.有48块糖,每袋装8块,可以装几袋? C.买9本同样的笔记本花了45元,每本笔记本多少钱? 问题2:为什么不选B,B也是用除法来解决的? 练习2:把相关数据填在相应的格子里。 (1)一千克猪肉18元,买5千克猪肉用去90元。 (2)每公顷工业用地售价10万元,买5公顷需要50万元。 (3)一箱可乐12瓶,每箱24元,每瓶2元,买了3箱共付72元。 讨论:这里的24元,为什么一会儿是单价,一会儿 是总价? 小结:任何一个条件在不同的问题情境中所表示数量的意义是可以变化的。 独立完成,校对 学生回答: 生1:足球每个40元是单价,6个是数量,要求共要多少钱是总价,所以可以用单价×数量=总价来解决。 生2:每次15元是单价,5次是数量,要多少钱是总价,所以也可以用单价×数量=总价来解决。 生3:一碗面10元是单价,100元是总价,要解决可以买几碗这样的面,要用总价÷单价=数量来解决。 学生回答: 生:A选项中的10元是总价,5支是数量,用总价÷数量=单价,能解决问题。C选项中45元是总价,9本是数量,用总价÷数量=单价也能解决问题,虽然B选项虽然能用除法解决,但48块不是总价,所以不符合这种数量关系。 学生独立填表 学生回答:每箱可乐24元,对于一瓶一瓶来说,它就是12瓶的总价;而对于3箱来说,这时24就是单价。 在初步获得总价模型的基础上,帮助学生掌握不同情境中单价、数量和总价的含义,并通过解决问题,培养灵活辨识数量关系的能力。 根据信息,结合三者数量关系,选择数据填表格,一方面促进学生解决问题能力的提升,另一方面,通过第三小题的辨析讨论让学生感受单价与总价的相对性,同时也能让学生体会解决问题时审题的重要性。
环节四 课堂小结 你有什么收获? 回顾本节课自己的体会和收获。 鼓励学生畅谈自己的收获和体会,加深对所学知识的理解和掌握。
环节六 布置作业 教材P52页做一做第2题,教材54页练习九第3题
1
