人教版四年级数学上册 第五单元第3课时点到直线的距离精品教学方案(表格式)
文档属性
| 名称 | 人教版四年级数学上册 第五单元第3课时点到直线的距离精品教学方案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 189.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-20 14:25:20 | ||
图片预览


文档简介
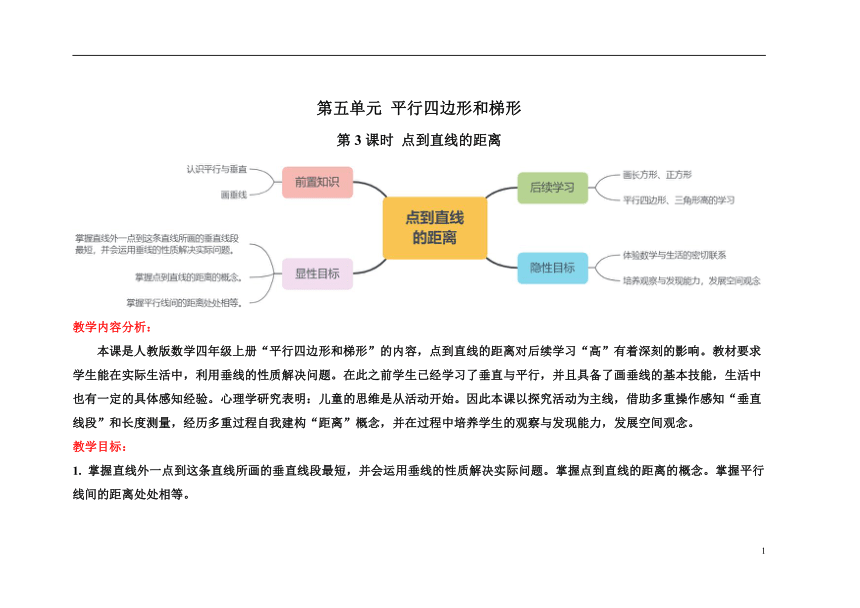
第五单元 平行四边形和梯形
点到直线的距离
教学内容分析:
本课是人教版数学四年级上册“平行四边形和梯形”的内容,点到直线的距离对后续学习“高”有着深刻的影响。教材要求学生能在实际生活中,利用垂线的性质解决问题。在此之前学生已经学习了垂直与平行,并且具备了画垂线的基本技能,生活中也有一定的具体感知经验。心理学研究表明:儿童的思维是从活动开始。因此本课以探究活动为主线,借助多重操作感知“垂直线段”和长度测量,经历多重过程自我建构“距离”概念,并在过程中培养学生的观察与发现能力,发展空间观念。
教学目标:
1. 掌握直线外一点到这条直线所画的垂直线段最短,并会运用垂线的性质解决实际问题。掌握点到直线的距离的概念。掌握平行线间的距离处处相等。
2. 经历垂直线段的性质的探索过程,进一步培养观察能力、实践能力,发展空间观念。
教学重点:
掌握垂线的性质、点到直线的距离、平行线间的距离处处相等。
教学难点:
明确直线外一点到这条直线的所有线段中垂直线段最短,能运用垂线的性质解决实际问题。掌握点到直线的距离的概念。
教学过程:
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 出示点A和直线m。 提问:同学们,从A点出发到直线m你能画出几条线段?线段的端点在哪里? 小结:从一个点出发到一条直线可以画无数条线段,起点都是点A,另一个端点都在直线上。 学生自由画线段,再选取两条线段指明端点。 让学生画从A点出发到直线m的线段,为后续学习作为基础材料。取材于学生,可以激发他们主动参与的积极性和好奇心。
环节二 探究新知 1.初步认识垂直线段 提问:仔细观察你们觉得哪条线段最特殊?特殊在哪儿? 共同验证垂直。 师:从点A到垂足D形成的线段叫做直线m的垂直线段。 讨论:哪条线段是直线BE的垂直线段? 师:线段AD真的垂直直线BE吗?我们来一起验证一下。 提问:那你能画出从A点出发到直线BE的垂直线段吗? 线段AD最特殊,因为它与直线m互相垂直。 直线AD。 通过三角板验证,发现未重合,否定线段AD。 学生动手画出正确的垂直线段,并展示交流。 先让学生在多个线段中自主发现特殊的线段,进而顺势告知垂直线段的含义。 学生多利用肉眼观察对垂直线段作出判断,这里故意设计不是垂直的情况,让学生再次感受垂直的本质,也让学生认识到工具的重要性。
2.加深感悟垂直线段 提问:在这些线段中,你认为哪条线段的长度最短?你能怎么证明? 验证后发现“垂直线段AF长度最短”的结论。 讨论:那这么多的线段中,还是垂直线段最短吗?可以怎么验证? 小结:从一点出发到直线的所有线段中,垂直线段最短,它的长度叫做这点到直线的距离。 讨论:要想知道从点B到直线m的距离是多少,你打算怎么办? 明确步骤:1、画出垂直线段;2、量出长度。 讨论:测量的6厘米指的是什么? 小结:点到直线的垂直线段的长度即点到直线的距离。 线段AF最短,可以量一量长度比一比。 ①直接比较可以看出越接近垂直线段,长度越短。 ②可以对靠近垂直线段的一些线段量一量再比较。 就是测量垂直线段的长度。 学生实际动手尝试。 ①6厘米是点B到直线m的垂直线段的长度。 ②6厘米是点B到直线m的距离。 从较少的线段中发现可以利用尺子测量比较的方法,再将多条线段的情况呈现,寻找更为合适的比较法和测量法。让学生完整感受“猜想——验证”的学习过程,培养严谨的学习习惯。 学生通过动手实践、交流辨析中发现点到直线的垂直线段的长度就是点到直线的距离,真正理解“距离”的含义。
3.操作感知平行 出示一组平行线 提问:已知a∥b,在a上任选3个点,分别向b画垂直的线段,并量一量这些线段的长度,你有什么发现吗? 小结:平行线间的距离处处相等。 长度都是相等的。 利用学生的实践活动,让其在自主探究中发现知识,完成建构,培养空间想象能力。
环节三 巩固练习 练习1:点A到直线DE的距离是( )? 练习2:下图中各组直线a、b是否互相平行? 练习3:从A点出发过斑马线,怎么过距离最短?把最短的路线画出来。 ② 学生通过画垂直线段进行测量。 练习一的设计主要是对距离概念的再次理解和辨别,对本课重点的再次巩固。 练习二是将视觉错觉和类似游戏形式的结合,是对平行线间的距离处处相等的运用。 练习三是让学生在生活中发现数学,并经历运用数学知识解决问题的过程,感受数学与生活的密切关系。
环节四 课堂小结 你有什么收获? ①从直线外一点到这条直线所画的所有线段中,垂直线段最短,它的长度叫做这点到直线的距离。 ②平行线间的距离处处相等。 鼓励学生畅谈自己的收获和体会。
环节五 布置作业 教材P62第6题,P63第11题。
1
点到直线的距离
教学内容分析:
本课是人教版数学四年级上册“平行四边形和梯形”的内容,点到直线的距离对后续学习“高”有着深刻的影响。教材要求学生能在实际生活中,利用垂线的性质解决问题。在此之前学生已经学习了垂直与平行,并且具备了画垂线的基本技能,生活中也有一定的具体感知经验。心理学研究表明:儿童的思维是从活动开始。因此本课以探究活动为主线,借助多重操作感知“垂直线段”和长度测量,经历多重过程自我建构“距离”概念,并在过程中培养学生的观察与发现能力,发展空间观念。
教学目标:
1. 掌握直线外一点到这条直线所画的垂直线段最短,并会运用垂线的性质解决实际问题。掌握点到直线的距离的概念。掌握平行线间的距离处处相等。
2. 经历垂直线段的性质的探索过程,进一步培养观察能力、实践能力,发展空间观念。
教学重点:
掌握垂线的性质、点到直线的距离、平行线间的距离处处相等。
教学难点:
明确直线外一点到这条直线的所有线段中垂直线段最短,能运用垂线的性质解决实际问题。掌握点到直线的距离的概念。
教学过程:
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 出示点A和直线m。 提问:同学们,从A点出发到直线m你能画出几条线段?线段的端点在哪里? 小结:从一个点出发到一条直线可以画无数条线段,起点都是点A,另一个端点都在直线上。 学生自由画线段,再选取两条线段指明端点。 让学生画从A点出发到直线m的线段,为后续学习作为基础材料。取材于学生,可以激发他们主动参与的积极性和好奇心。
环节二 探究新知 1.初步认识垂直线段 提问:仔细观察你们觉得哪条线段最特殊?特殊在哪儿? 共同验证垂直。 师:从点A到垂足D形成的线段叫做直线m的垂直线段。 讨论:哪条线段是直线BE的垂直线段? 师:线段AD真的垂直直线BE吗?我们来一起验证一下。 提问:那你能画出从A点出发到直线BE的垂直线段吗? 线段AD最特殊,因为它与直线m互相垂直。 直线AD。 通过三角板验证,发现未重合,否定线段AD。 学生动手画出正确的垂直线段,并展示交流。 先让学生在多个线段中自主发现特殊的线段,进而顺势告知垂直线段的含义。 学生多利用肉眼观察对垂直线段作出判断,这里故意设计不是垂直的情况,让学生再次感受垂直的本质,也让学生认识到工具的重要性。
2.加深感悟垂直线段 提问:在这些线段中,你认为哪条线段的长度最短?你能怎么证明? 验证后发现“垂直线段AF长度最短”的结论。 讨论:那这么多的线段中,还是垂直线段最短吗?可以怎么验证? 小结:从一点出发到直线的所有线段中,垂直线段最短,它的长度叫做这点到直线的距离。 讨论:要想知道从点B到直线m的距离是多少,你打算怎么办? 明确步骤:1、画出垂直线段;2、量出长度。 讨论:测量的6厘米指的是什么? 小结:点到直线的垂直线段的长度即点到直线的距离。 线段AF最短,可以量一量长度比一比。 ①直接比较可以看出越接近垂直线段,长度越短。 ②可以对靠近垂直线段的一些线段量一量再比较。 就是测量垂直线段的长度。 学生实际动手尝试。 ①6厘米是点B到直线m的垂直线段的长度。 ②6厘米是点B到直线m的距离。 从较少的线段中发现可以利用尺子测量比较的方法,再将多条线段的情况呈现,寻找更为合适的比较法和测量法。让学生完整感受“猜想——验证”的学习过程,培养严谨的学习习惯。 学生通过动手实践、交流辨析中发现点到直线的垂直线段的长度就是点到直线的距离,真正理解“距离”的含义。
3.操作感知平行 出示一组平行线 提问:已知a∥b,在a上任选3个点,分别向b画垂直的线段,并量一量这些线段的长度,你有什么发现吗? 小结:平行线间的距离处处相等。 长度都是相等的。 利用学生的实践活动,让其在自主探究中发现知识,完成建构,培养空间想象能力。
环节三 巩固练习 练习1:点A到直线DE的距离是( )? 练习2:下图中各组直线a、b是否互相平行? 练习3:从A点出发过斑马线,怎么过距离最短?把最短的路线画出来。 ② 学生通过画垂直线段进行测量。 练习一的设计主要是对距离概念的再次理解和辨别,对本课重点的再次巩固。 练习二是将视觉错觉和类似游戏形式的结合,是对平行线间的距离处处相等的运用。 练习三是让学生在生活中发现数学,并经历运用数学知识解决问题的过程,感受数学与生活的密切关系。
环节四 课堂小结 你有什么收获? ①从直线外一点到这条直线所画的所有线段中,垂直线段最短,它的长度叫做这点到直线的距离。 ②平行线间的距离处处相等。 鼓励学生畅谈自己的收获和体会。
环节五 布置作业 教材P62第6题,P63第11题。
1
