提公因式法[下学期]

课件9张PPT。提公因式法用简便方法计算
（1）13.7 х17/31 +19.8 х 17/31 –2.5 х 17/31
（2）57.6 х 1.6+28.8 х36.8–14.4 х80解：（1）原式= 17/31 х （13.7+19.8 –2.5） （2）原式=57.6 х1.6+28.8 х2 х18.4–14.4 х4 х20= 17/31 х 31
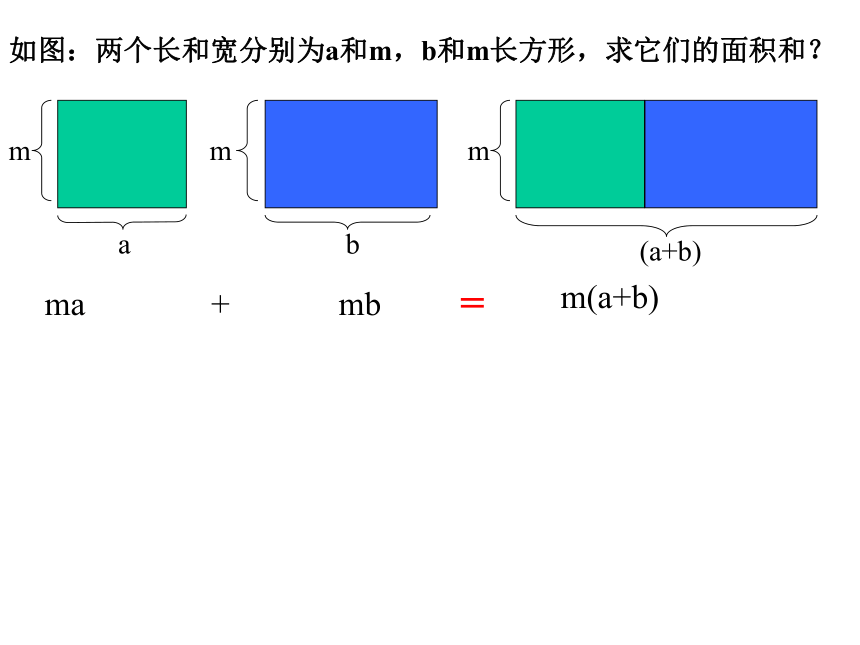
=17=57.6 х1.6+57.6 х18.4 – 57.6 х20=57.6 х（1.6+18.4 –20）=0(a+b)如图：两个长和宽分别为a和m，b和m长方形，求它们的面积和？ma + mbm(a+b)=提问：（1）多项式ab –ac+ad中有相同的因式吗？多项式3x2+x呢？
多项式mb2+nb –b呢？
(2) 上面的多项式都可以写成几个因式的乘积的形式吗？
试试看。我们把多项式中各项都含有的相同因式叫做这个多项式的公因式。讨论：多项式x2+6x3中各项的公因式是什么？多项式2x2+6x3中各
项的公因式呢？你能归纳出如何找出多项式中的公因式吗？ab –ac+ad=a(b – c+d)3x2+x=x(3x+1)mb2+nb – b=b(mb+n –1) 如果一个多项式的各项含有公因式，那么
就可以把这个公因式提出来，从而将多项式
化成两个因式乘积的形式，这种分解因式的
方法叫做提公因式法。 多项式中的公因式是指各项中都含有的因式，如果各项系
数是整系数，则取系数的最大公约数；如果各项中相同的因式
（字母或多项式）的次数不同，则取次数最低的那个相同因式；
所有这些因式的乘积即为公因式。2x2+6x3x2+6x3x22x2例、将下列各式分解因式：
（1）4x+12y (2)7a3b2 – 12ab3c
(3)3ma4 – 6ma2 – 9ma (4) – 4m3+16m2 – 26m
(5)am+1+a2m – am (6)3(a+b)m – 1 – (a+b)m解： （1）原式= 4x+4 х3y
=4(x+3y)(2)原式= ab2.7a2 –ab2.12bc(3)原式=3ma.a3 – 3ma.2a – 3ma.3(4)原式= – (4m3 – 16m2 +26m)(5)原式=am . a+am . am –am(6)原式=3(a+b)m –1 –(a+b)m –1(a+b) =ab2(7a2 –12bc) =3ma(a3 – 2a – 3)= –(2m.2m2 –2m.8m+2m.13) = –2m(2m2 –8m+13)=am(a+am –1)=(a+b)m –1 ［ 3 –(a+b)］= (a+b)m –1 ( 3 –a – b) 练习：把下列各式分解因式；
(1)ma+mb= (2)4kx –8ky=
(3)5y3+20y2= (4)a2b –2ab2+ab=
(5)8x –72= (6)a2b –5ab=
(7)4m3 –6m2= (8)a2b –5ab+9b=
(9) –a2+ab –ac=
(10) –2x3+4x2+2x=m(a+b)4k(x – 2y)5y2(y+4)ab(a –2b+1)8(x –9)ab(a –5)2m2(2m –3)b(a2 –5a+9)–a(a –b+c)–2x(x2 –2x –1)思考：提取公因式法分解因式与单项式乘多项式有什么关系？小结 提公因式法分解因式的一般步骤：（1）若各项系数是整系数，取系数的最大公约数；（2）取相同的字母，字母的指数取较低的；（3）取相同的多项式，多项式的指数取较低的；（4）所有这些因式的乘积即为公因式；作业：P44
习题2.2 1、 (5).(6).(7).(8)
2