人教版数学九年级第二学期 期末复习卷(含答案)
文档属性
| 名称 | 人教版数学九年级第二学期 期末复习卷(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-20 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
九年级数学期末复习卷(1)
一.选择题(共10小题)
1.观察下列图形,是中心对称图形的是( )
A. B. C. D.
2.下列运算正确的是( )
A.a2+a3=a5 B.a2 a3=a6 C.(2a)3=8a3 D.a3÷a=a3
3.方程(x+1)2=4的解是( )
A.x1=2,x2=﹣2 B.x1=3,x2=﹣3 C.x1=1,x2=﹣3 D.x1=1,x2=﹣2
4.将二次函数y=(x﹣1)2+2的图象向上平移3个单位长度,再向右平移4个单位长度,得到的抛物线的函数表达式为( )
A.y=(x+3)2+5 B.y=(x﹣5)2﹣1 C.y=(x﹣5)2+5 D.y=(x+5)2﹣5
5.将抛物线y=x2﹣2向左平移3个单位长度,再向上平移3个单位长度后,所得抛物线的解析式为( )
A.y=(x+3)2+3 B.y=(x﹣3)2+1 C.y=(x+2)2+1 D.y=(x+3)2+1
6.如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )
A.130° B.100° C.80° D.50°
7.在同一平面直角坐标系中,函数y=ax2+bx与y=﹣bx+a的图象可能是( )
A. B.
C. D.
8.如图,菱形ABCD的边长为4,且AE⊥BC,E、F、G、H分别为BC、CD、DA、AB的中点,以A、B、C、D四点为圆心,半径为2作圆,则图中阴影部分的面积是( )
A.4﹣4π B.4﹣2π
C.8﹣2π D.8﹣4π
9.如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),
半径为3,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是( )
10题图
A.4 B. C. D.
10.如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
A. B. C. D.12
二.填空题(共6小题)
11.已知一元二次方程x2+kx﹣7=0有一根为1,则k的值为 .
12.有一组数:,,,,…,则第n个数为 .(用含n的代数式表示)
13.若抛物线y=2x2﹣px+4p+1中不管p取何值时都通过定点,则定点坐标为 .
14.如图,用一个圆心角为120°的扇形围成一个无底的圆锥,如果这个圆锥底面圆的半径为1cm,则这个扇形的半径是 cm.
15题图
15.已知等边△ABC的边长为4,点P是边BC上的动点,将△ABP绕点A逆时针旋转60°得到△ACQ,点D是AC边的中点,连接DQ,则DQ的最小值是 .
16.二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③,3a+c>0;④当x>﹣1时,y的值随x值的增大而增大;⑤4a+2b≥am2+bm(m为任意实数).其中正确的结论有 .(填序号)
三.解答题(共8小题)
17.先化简,再求值:,其中x满足方程x2﹣x﹣6=0.
18.已知关于x的方程x2﹣mx+m﹣1=0.
(1)求证:无论m取任何实数时,方程恒有实数根.
(2)任取一个你喜欢的m值代入,并求出此时方程的根.
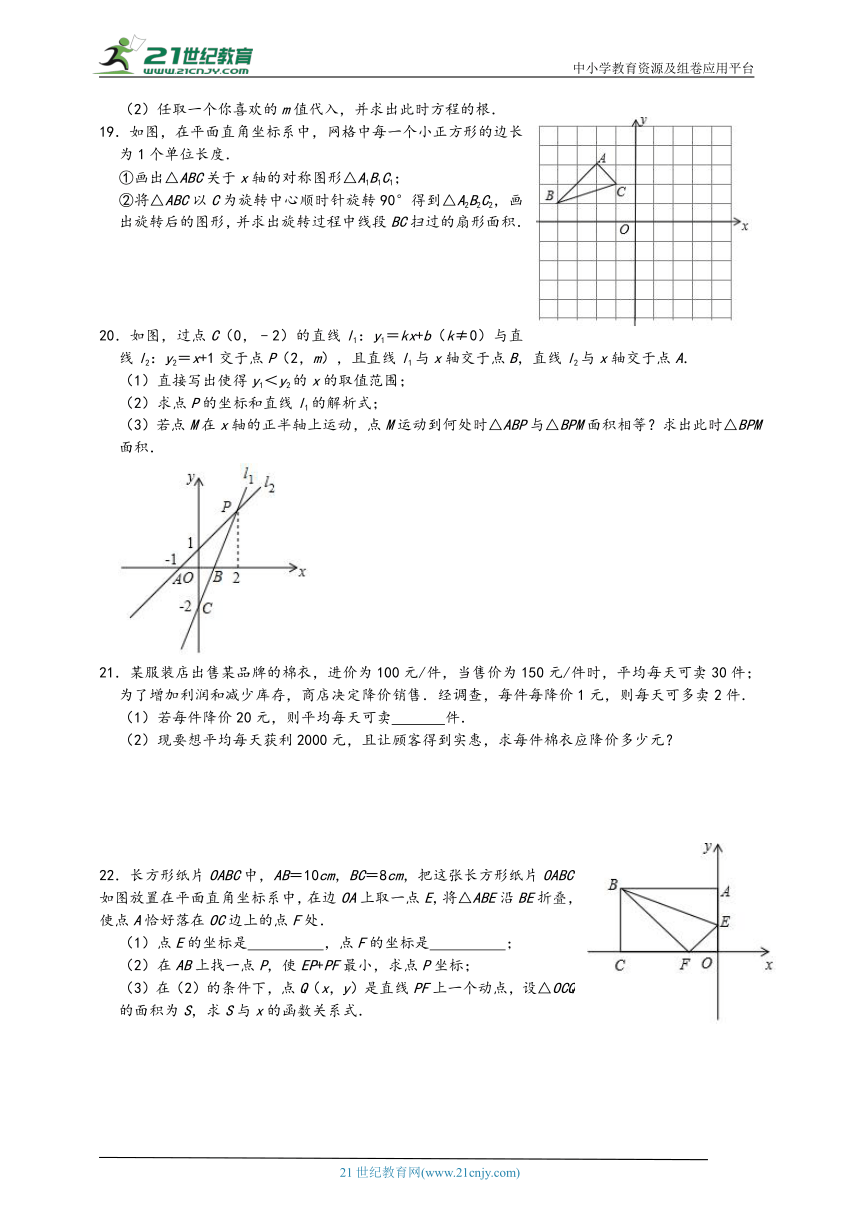
19.如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度.
①画出△ABC关于x轴的对称图形△A1B1C1;
②将△ABC以C为旋转中心顺时针旋转90°得到△A2B2C2,画出旋转后的图形,并求出旋转过程中线段BC扫过的扇形面积.
20.如图,过点C(0,﹣2)的直线l1:y1=kx+b(k≠0)与直线l2:y2=x+1交于点P(2,m),且直线l1与x轴交于点B,直线l2与x轴交于点A.
(1)直接写出使得y1<y2的x的取值范围;
(2)求点P的坐标和直线l1的解析式;
(3)若点M在x轴的正半轴上运动,点M运动到何处时△ABP与△BPM面积相等?求出此时△BPM面积.
21.某服装店出售某品牌的棉衣,进价为100元/件,当售价为150元/件时,平均每天可卖30件;为了增加利润和减少库存,商店决定降价销售.经调查,每件每降价1元,则每天可多卖2件.
(1)若每件降价20元,则平均每天可卖 件.
(2)现要想平均每天获利2000元,且让顾客得到实惠,求每件棉衣应降价多少元?
22.长方形纸片OABC中,AB=10cm,BC=8cm,把这张长方形纸片OABC如图放置在平面直角坐标系中,在边OA上取一点E,将△ABE沿BE折叠,使点A恰好落在OC边上的点F处.
(1)点E的坐标是 ,点F的坐标是 ;
(2)在AB上找一点P,使EP+PF最小,求点P坐标;
(3)在(2)的条件下,点Q(x,y)是直线PF上一个动点,设△OCQ的面积为S,求S与x的函数关系式.
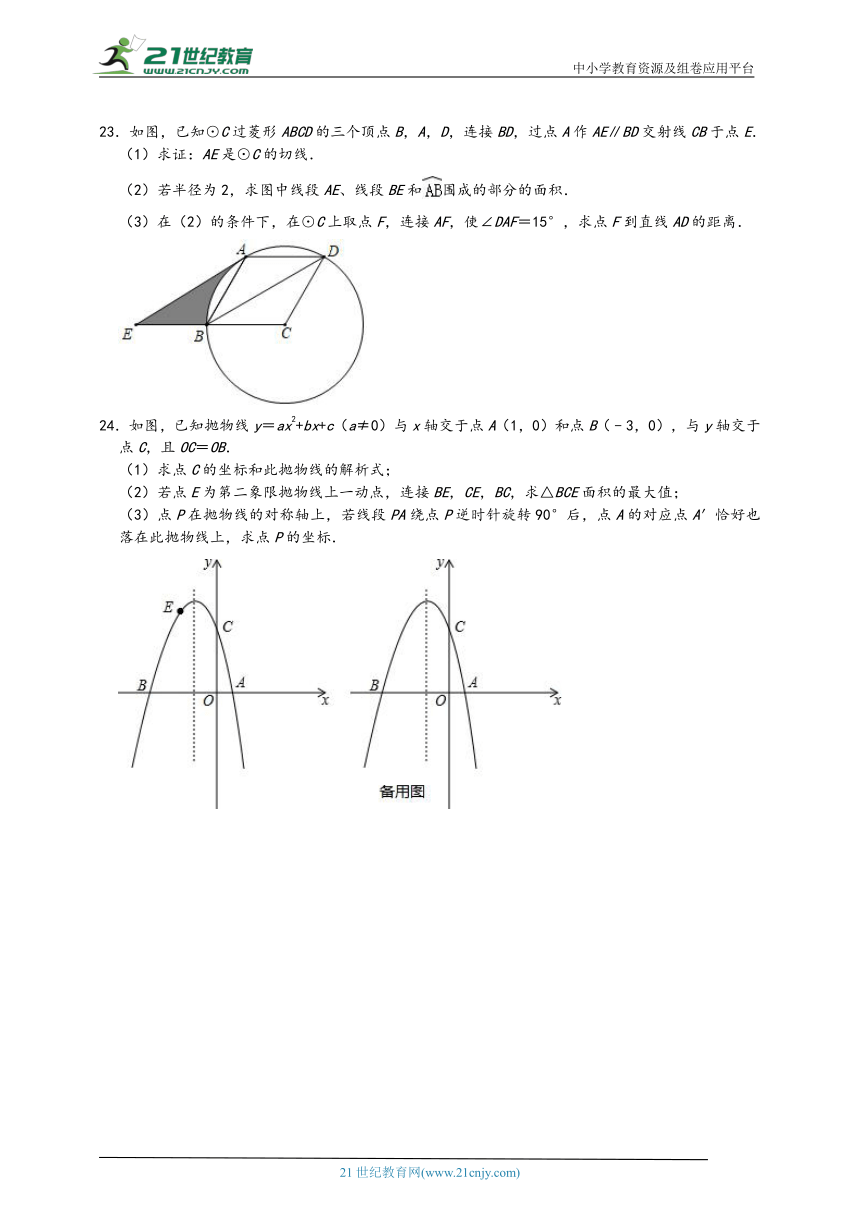
23.如图,已知⊙C过菱形ABCD的三个顶点B,A,D,连接BD,过点A作AE∥BD交射线CB于点E.
(1)求证:AE是⊙C的切线.
(2)若半径为2,求图中线段AE、线段BE和围成的部分的面积.
(3)在(2)的条件下,在⊙C上取点F,连接AF,使∠DAF=15°,求点F到直线AD的距离.
24.如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
(1)求点C的坐标和此抛物线的解析式;
(2)若点E为第二象限抛物线上一动点,连接BE,CE,BC,求△BCE面积的最大值;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
参考答案
一.选择题(共10小题)
1.C.2.C.3.C.4.C.5.D.6.A.7.A.8.D.9.B.10.C.
二.填空题(共6小题)
11.6.12..13.(4,33).14.3.15..16 ①③⑤ .(填序号)
三.解答题(共8小题)
17.解:
=()
=
=x+3,
由方程x2﹣x﹣6=0,可得x1=3,x2=﹣2,
当x=3时,原分式无意义,
∴x=﹣2,
当x=﹣2时,原式=﹣2+3=1.
18.(1)证明:∵Δ=(﹣m)2﹣4(m﹣1)=(m﹣2)2≥0,
∴无论m取任何实数时,方程恒有实数根.
(2)解:当m=0时,方程x2﹣mx+m﹣1=0为方程x2﹣1=0,
解得x1=﹣1,x2=1.
故m=0时,方程的根是x1=﹣1,x2=1.
19.解:①如图所示,△A1B1C1即为所求;
②如图所示,△A2B2C2即为旋转后的图形,
由题可得,BC=,
∴线段BC扫过的扇形面积为=.
20.解:(1)当x<2时,y1<y2;
(2)把点P(2,m)代入y2=x+1中,得m=2+1=3,
∴点P的坐标为(2,3).
把点C(0,﹣2)、P(2,3)分别代入y1=kx+b中,得
,解得,
∴直线l1的解析式为y1=x﹣2;
(3)由(2)得点P的坐标为(2,3),
∵△ABP与△BPM有相同的高,即h=3.要使△ABP与△BPM面积相等,且点M在x轴正半轴上.
∴在x轴上取点M,当AB=BM时,△ABP与△BPM面积相等.
∵在直线中,当y=0时,,即点B的坐标是(,0),
∴AB=1+=,BM=OM﹣OB=,
∴OM=,则点M运动到(,0)时△ABP与△BPM面积相等.
∴S△BPM=.
21.解:(1)30+20×2=70件,
故答案为:70;
(2)设每件棉衣降价x元,则日销售量是(30+2x)件
依题意可得:(150﹣100﹣x)(30+2x)=2000
解得x1=10,x2=25
为了使顾客得到实惠,舍去x1=10
答:每件棉衣降价25元.
22.解:(1)设OE=x,则AE=8﹣x,
由折叠知BA=BF=10,EF=AE=8﹣x,
∵四边形OABC是长方形,
∴∠BCO=90°,
∴CF==6,
∴OF=OC﹣CF=10﹣6=4,
∴点F的坐标为(﹣4,0),
在Rt△EOF中,EF2=OF2+OE2,即(8﹣x)2=42+x2,
解得,x=3,
∴点E的坐标为(0,3),
∴点E的坐标为(0,3),点F的坐标为(﹣4,0).
故答案为(0,3),(﹣4,0).
(2)作E关于AB的对称点E′,连接FE′,交AB于P,则PE+PF最小最小,
∵点E的坐标为(0,3),
∴AE=8﹣3=5,
∵点E与点E′关于AB对称,
∴AE′=AE=5,
∴OE′=5+8=13,
∴点E′的坐标为(0,13),
设直线FE′的解析式为y=kx+b,
则,
解得,k=,b=13,
则直线FE′的解析式为y=x+13,
当y=8时,x+13=8,
解得,x=﹣,
∴点P的坐标为(﹣,8);
(3)设点Q的坐标为(x,x+13),
当Q在x轴上方时,即x>﹣4时,S=×10×(x+13)=x+65,
当Q在x轴下方时,即x<﹣4时,S=×10×(﹣x﹣13)=﹣x﹣65,
综上所述,S=.
23.(1)证明:如图1中,连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,
又∵BD∥AE,
∴AC⊥AE,
∴AE是⊙O的切线.
(2)如图1中,∵四边形ABCD是菱形,
∴AB=BC,
又∵AC=BC,
∴△ABC是等边三角形,
∴∠ACB=60°,
∵AC=2,
∴AE=AC tan60°=2,
∴S阴=S△AEC﹣S扇形ACB=×2×2﹣=2﹣π.
(3)①如图2中,当点F在上时,
∵∠DAF=15°,
∴∠DCF=30°,
∵∠ACD=60°,
∴∠ACF=∠FCD,
∴点F是弧AD的中点,
∴CF⊥AD,
∴点F到直线AD的距离=CF﹣CA cos30°=2﹣.
②如图3中,当点F在优弧上时,
∵∠DAF=15°,
∴∠DCF=30°,
过点C作CG⊥AD于D,过点F作FH⊥CG于H,
可得∠AFH=15°,∠HFC=30°,
∴CH=1,
∴点F到直线AD的距离=CG﹣CH=AC cos30°﹣CH=﹣1.
综上所述,满足条件的点F到直线AD的距离为2﹣或﹣1.
24.解:(1)∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),
∴OB=3,
∵OC=OB,
∴OC=3,
∴c=3,
∴,
解得:,
∴所求抛物线解析式为:y=﹣x2﹣2x+3,C(0,3).
(2)如图2,连接BC,过点E作EF⊥x轴于点F,设E(a,﹣a2﹣2a+3)(﹣3<a<0),
∴EF=﹣a2﹣2a+3,BF=a+3,OF=﹣a,
∴S△BEC=S四边形BOCE﹣S△BOC=BF EF+(OC+EF) OF﹣ OB OC
=(a+3) (﹣a2﹣2a+3)+(﹣a2﹣2a+6) (﹣a)﹣
=﹣a2﹣a
=﹣(a+)2+,
∴当a=﹣时,S△BEC最大,且最大值为.
(3)∵抛物线y=﹣x2﹣2x+3的对称轴为x=﹣1,点P在抛物线的对称轴上,
∴设P(﹣1,m),
∵线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,
①当m≥0时,
∴PA=PA′,∠APA′=90°,
如图3,过A′作A′N⊥对称轴于N,设对称轴于x轴交于点M,
∴∠NPA′+∠MPA=∠NA′P+∠NPA′=90°,
∴∠NA′P=∠NPA,
在△A′NP与△PMA中,
,
∴△A′NP≌△PMA(AAS),
∴A′N=PM=m,PN=AM=2,
∴A′(m﹣1,m+2),
代入y=﹣x2﹣2x+3得:m+2=﹣(m﹣1)2﹣2(m﹣1)+3,
解得:m=1,m=﹣2(舍去),
②当m<0时,要使P2A=P2A2,由图可知A2点与B点重合,
∵∠AP2A2=90°,
∴MP2=MA=2,
∴P2(﹣1,﹣2).
∴满足条件的点P的坐标为P(﹣1,1)或(﹣1,﹣2).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学期末复习卷(1)
一.选择题(共10小题)
1.观察下列图形,是中心对称图形的是( )
A. B. C. D.
2.下列运算正确的是( )
A.a2+a3=a5 B.a2 a3=a6 C.(2a)3=8a3 D.a3÷a=a3
3.方程(x+1)2=4的解是( )
A.x1=2,x2=﹣2 B.x1=3,x2=﹣3 C.x1=1,x2=﹣3 D.x1=1,x2=﹣2
4.将二次函数y=(x﹣1)2+2的图象向上平移3个单位长度,再向右平移4个单位长度,得到的抛物线的函数表达式为( )
A.y=(x+3)2+5 B.y=(x﹣5)2﹣1 C.y=(x﹣5)2+5 D.y=(x+5)2﹣5
5.将抛物线y=x2﹣2向左平移3个单位长度,再向上平移3个单位长度后,所得抛物线的解析式为( )
A.y=(x+3)2+3 B.y=(x﹣3)2+1 C.y=(x+2)2+1 D.y=(x+3)2+1
6.如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )
A.130° B.100° C.80° D.50°
7.在同一平面直角坐标系中,函数y=ax2+bx与y=﹣bx+a的图象可能是( )
A. B.
C. D.
8.如图,菱形ABCD的边长为4,且AE⊥BC,E、F、G、H分别为BC、CD、DA、AB的中点,以A、B、C、D四点为圆心,半径为2作圆,则图中阴影部分的面积是( )
A.4﹣4π B.4﹣2π
C.8﹣2π D.8﹣4π
9.如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),
半径为3,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是( )
10题图
A.4 B. C. D.
10.如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
A. B. C. D.12
二.填空题(共6小题)
11.已知一元二次方程x2+kx﹣7=0有一根为1,则k的值为 .
12.有一组数:,,,,…,则第n个数为 .(用含n的代数式表示)
13.若抛物线y=2x2﹣px+4p+1中不管p取何值时都通过定点,则定点坐标为 .
14.如图,用一个圆心角为120°的扇形围成一个无底的圆锥,如果这个圆锥底面圆的半径为1cm,则这个扇形的半径是 cm.
15题图
15.已知等边△ABC的边长为4,点P是边BC上的动点,将△ABP绕点A逆时针旋转60°得到△ACQ,点D是AC边的中点,连接DQ,则DQ的最小值是 .
16.二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③,3a+c>0;④当x>﹣1时,y的值随x值的增大而增大;⑤4a+2b≥am2+bm(m为任意实数).其中正确的结论有 .(填序号)
三.解答题(共8小题)
17.先化简,再求值:,其中x满足方程x2﹣x﹣6=0.
18.已知关于x的方程x2﹣mx+m﹣1=0.
(1)求证:无论m取任何实数时,方程恒有实数根.
(2)任取一个你喜欢的m值代入,并求出此时方程的根.
19.如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度.
①画出△ABC关于x轴的对称图形△A1B1C1;
②将△ABC以C为旋转中心顺时针旋转90°得到△A2B2C2,画出旋转后的图形,并求出旋转过程中线段BC扫过的扇形面积.
20.如图,过点C(0,﹣2)的直线l1:y1=kx+b(k≠0)与直线l2:y2=x+1交于点P(2,m),且直线l1与x轴交于点B,直线l2与x轴交于点A.
(1)直接写出使得y1<y2的x的取值范围;
(2)求点P的坐标和直线l1的解析式;
(3)若点M在x轴的正半轴上运动,点M运动到何处时△ABP与△BPM面积相等?求出此时△BPM面积.
21.某服装店出售某品牌的棉衣,进价为100元/件,当售价为150元/件时,平均每天可卖30件;为了增加利润和减少库存,商店决定降价销售.经调查,每件每降价1元,则每天可多卖2件.
(1)若每件降价20元,则平均每天可卖 件.
(2)现要想平均每天获利2000元,且让顾客得到实惠,求每件棉衣应降价多少元?
22.长方形纸片OABC中,AB=10cm,BC=8cm,把这张长方形纸片OABC如图放置在平面直角坐标系中,在边OA上取一点E,将△ABE沿BE折叠,使点A恰好落在OC边上的点F处.
(1)点E的坐标是 ,点F的坐标是 ;
(2)在AB上找一点P,使EP+PF最小,求点P坐标;
(3)在(2)的条件下,点Q(x,y)是直线PF上一个动点,设△OCQ的面积为S,求S与x的函数关系式.
23.如图,已知⊙C过菱形ABCD的三个顶点B,A,D,连接BD,过点A作AE∥BD交射线CB于点E.
(1)求证:AE是⊙C的切线.
(2)若半径为2,求图中线段AE、线段BE和围成的部分的面积.
(3)在(2)的条件下,在⊙C上取点F,连接AF,使∠DAF=15°,求点F到直线AD的距离.
24.如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
(1)求点C的坐标和此抛物线的解析式;
(2)若点E为第二象限抛物线上一动点,连接BE,CE,BC,求△BCE面积的最大值;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
参考答案
一.选择题(共10小题)
1.C.2.C.3.C.4.C.5.D.6.A.7.A.8.D.9.B.10.C.
二.填空题(共6小题)
11.6.12..13.(4,33).14.3.15..16 ①③⑤ .(填序号)
三.解答题(共8小题)
17.解:
=()
=
=x+3,
由方程x2﹣x﹣6=0,可得x1=3,x2=﹣2,
当x=3时,原分式无意义,
∴x=﹣2,
当x=﹣2时,原式=﹣2+3=1.
18.(1)证明:∵Δ=(﹣m)2﹣4(m﹣1)=(m﹣2)2≥0,
∴无论m取任何实数时,方程恒有实数根.
(2)解:当m=0时,方程x2﹣mx+m﹣1=0为方程x2﹣1=0,
解得x1=﹣1,x2=1.
故m=0时,方程的根是x1=﹣1,x2=1.
19.解:①如图所示,△A1B1C1即为所求;
②如图所示,△A2B2C2即为旋转后的图形,
由题可得,BC=,
∴线段BC扫过的扇形面积为=.
20.解:(1)当x<2时,y1<y2;
(2)把点P(2,m)代入y2=x+1中,得m=2+1=3,
∴点P的坐标为(2,3).
把点C(0,﹣2)、P(2,3)分别代入y1=kx+b中,得
,解得,
∴直线l1的解析式为y1=x﹣2;
(3)由(2)得点P的坐标为(2,3),
∵△ABP与△BPM有相同的高,即h=3.要使△ABP与△BPM面积相等,且点M在x轴正半轴上.
∴在x轴上取点M,当AB=BM时,△ABP与△BPM面积相等.
∵在直线中,当y=0时,,即点B的坐标是(,0),
∴AB=1+=,BM=OM﹣OB=,
∴OM=,则点M运动到(,0)时△ABP与△BPM面积相等.
∴S△BPM=.
21.解:(1)30+20×2=70件,
故答案为:70;
(2)设每件棉衣降价x元,则日销售量是(30+2x)件
依题意可得:(150﹣100﹣x)(30+2x)=2000
解得x1=10,x2=25
为了使顾客得到实惠,舍去x1=10
答:每件棉衣降价25元.
22.解:(1)设OE=x,则AE=8﹣x,
由折叠知BA=BF=10,EF=AE=8﹣x,
∵四边形OABC是长方形,
∴∠BCO=90°,
∴CF==6,
∴OF=OC﹣CF=10﹣6=4,
∴点F的坐标为(﹣4,0),
在Rt△EOF中,EF2=OF2+OE2,即(8﹣x)2=42+x2,
解得,x=3,
∴点E的坐标为(0,3),
∴点E的坐标为(0,3),点F的坐标为(﹣4,0).
故答案为(0,3),(﹣4,0).
(2)作E关于AB的对称点E′,连接FE′,交AB于P,则PE+PF最小最小,
∵点E的坐标为(0,3),
∴AE=8﹣3=5,
∵点E与点E′关于AB对称,
∴AE′=AE=5,
∴OE′=5+8=13,
∴点E′的坐标为(0,13),
设直线FE′的解析式为y=kx+b,
则,
解得,k=,b=13,
则直线FE′的解析式为y=x+13,
当y=8时,x+13=8,
解得,x=﹣,
∴点P的坐标为(﹣,8);
(3)设点Q的坐标为(x,x+13),
当Q在x轴上方时,即x>﹣4时,S=×10×(x+13)=x+65,
当Q在x轴下方时,即x<﹣4时,S=×10×(﹣x﹣13)=﹣x﹣65,
综上所述,S=.
23.(1)证明:如图1中,连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,
又∵BD∥AE,
∴AC⊥AE,
∴AE是⊙O的切线.
(2)如图1中,∵四边形ABCD是菱形,
∴AB=BC,
又∵AC=BC,
∴△ABC是等边三角形,
∴∠ACB=60°,
∵AC=2,
∴AE=AC tan60°=2,
∴S阴=S△AEC﹣S扇形ACB=×2×2﹣=2﹣π.
(3)①如图2中,当点F在上时,
∵∠DAF=15°,
∴∠DCF=30°,
∵∠ACD=60°,
∴∠ACF=∠FCD,
∴点F是弧AD的中点,
∴CF⊥AD,
∴点F到直线AD的距离=CF﹣CA cos30°=2﹣.
②如图3中,当点F在优弧上时,
∵∠DAF=15°,
∴∠DCF=30°,
过点C作CG⊥AD于D,过点F作FH⊥CG于H,
可得∠AFH=15°,∠HFC=30°,
∴CH=1,
∴点F到直线AD的距离=CG﹣CH=AC cos30°﹣CH=﹣1.
综上所述,满足条件的点F到直线AD的距离为2﹣或﹣1.
24.解:(1)∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),
∴OB=3,
∵OC=OB,
∴OC=3,
∴c=3,
∴,
解得:,
∴所求抛物线解析式为:y=﹣x2﹣2x+3,C(0,3).
(2)如图2,连接BC,过点E作EF⊥x轴于点F,设E(a,﹣a2﹣2a+3)(﹣3<a<0),
∴EF=﹣a2﹣2a+3,BF=a+3,OF=﹣a,
∴S△BEC=S四边形BOCE﹣S△BOC=BF EF+(OC+EF) OF﹣ OB OC
=(a+3) (﹣a2﹣2a+3)+(﹣a2﹣2a+6) (﹣a)﹣
=﹣a2﹣a
=﹣(a+)2+,
∴当a=﹣时,S△BEC最大,且最大值为.
(3)∵抛物线y=﹣x2﹣2x+3的对称轴为x=﹣1,点P在抛物线的对称轴上,
∴设P(﹣1,m),
∵线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,
①当m≥0时,
∴PA=PA′,∠APA′=90°,
如图3,过A′作A′N⊥对称轴于N,设对称轴于x轴交于点M,
∴∠NPA′+∠MPA=∠NA′P+∠NPA′=90°,
∴∠NA′P=∠NPA,
在△A′NP与△PMA中,
,
∴△A′NP≌△PMA(AAS),
∴A′N=PM=m,PN=AM=2,
∴A′(m﹣1,m+2),
代入y=﹣x2﹣2x+3得:m+2=﹣(m﹣1)2﹣2(m﹣1)+3,
解得:m=1,m=﹣2(舍去),
②当m<0时,要使P2A=P2A2,由图可知A2点与B点重合,
∵∠AP2A2=90°,
∴MP2=MA=2,
∴P2(﹣1,﹣2).
∴满足条件的点P的坐标为P(﹣1,1)或(﹣1,﹣2).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
