27.3 位似(1) 课件(共38张PPT) 2022—2023学年人教版数学九年级下册
文档属性
| 名称 | 27.3 位似(1) 课件(共38张PPT) 2022—2023学年人教版数学九年级下册 |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 15:29:32 | ||
图片预览


文档简介
(共38张PPT)
27.3位似(1)
位似图形
位似图形
位似图形
位似图形
在幻灯机上放映幻灯片时,把幻灯片上的图象放大到屏幕上
在照相馆里,摄影师通过照相机把实物的图象缩小在底片上
这样放大或缩小的图形,形状_____,大小______,所以它们_____.
相同
不同
相似
放映机
D
E
F
A
O
B
C
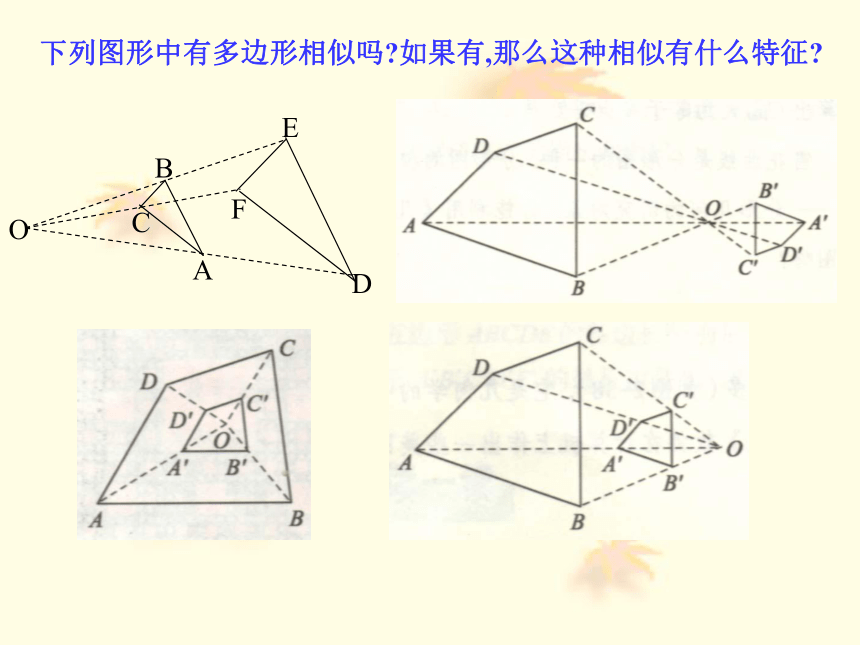
下列图形中有多边形相似吗 如果有,那么这种相似有什么特征
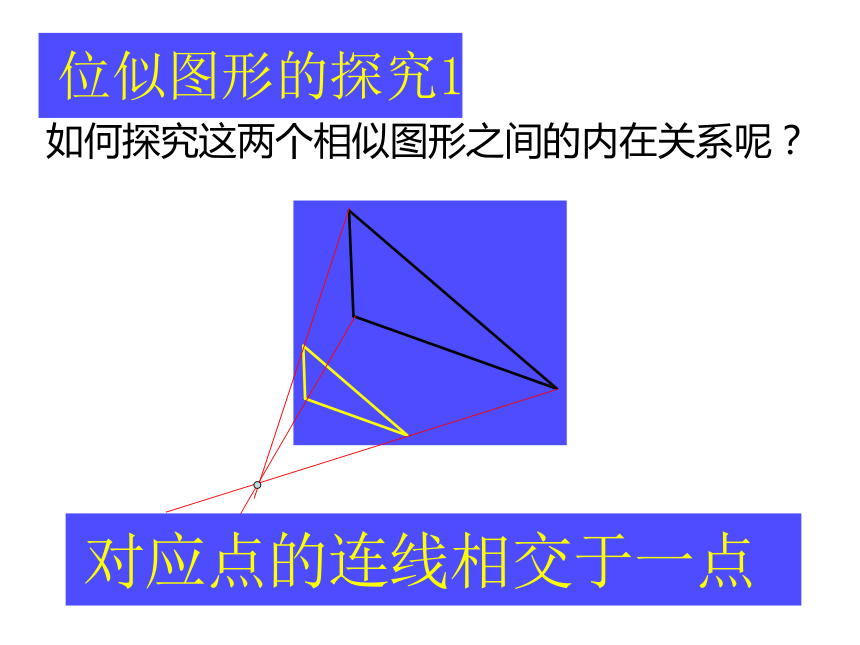
如何探究这两个相似图形之间的内在关系呢?
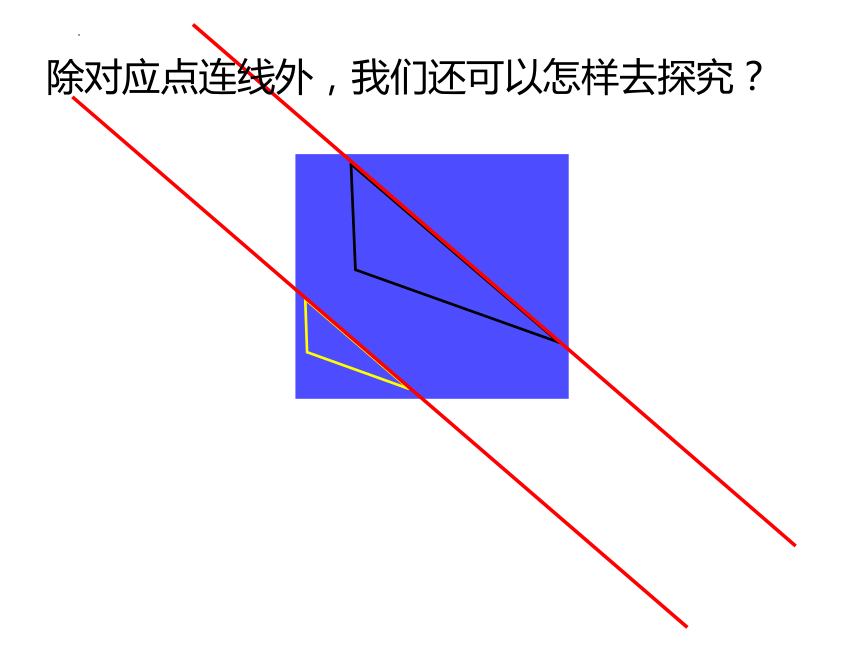
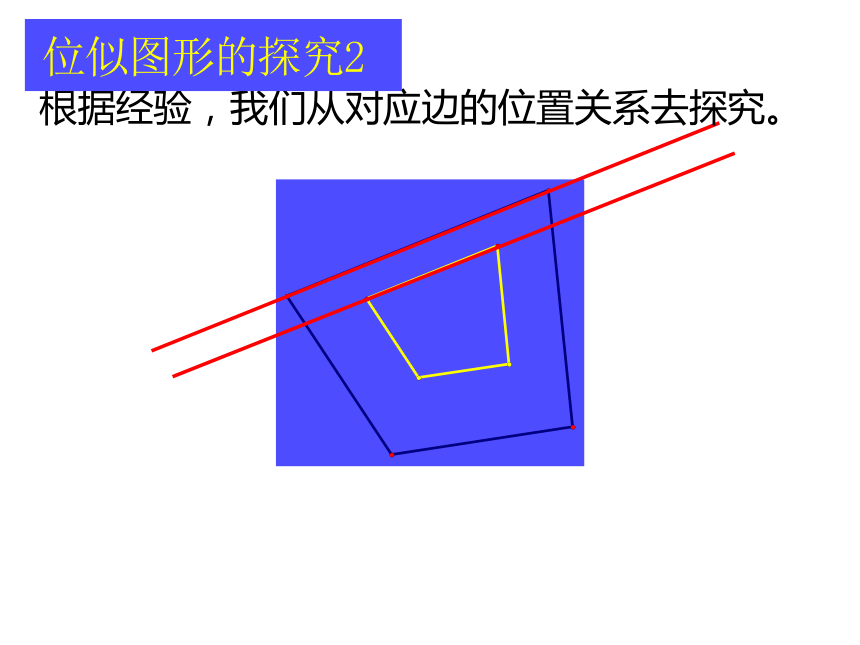
除对应点连线外,我们还可以怎样去探究?
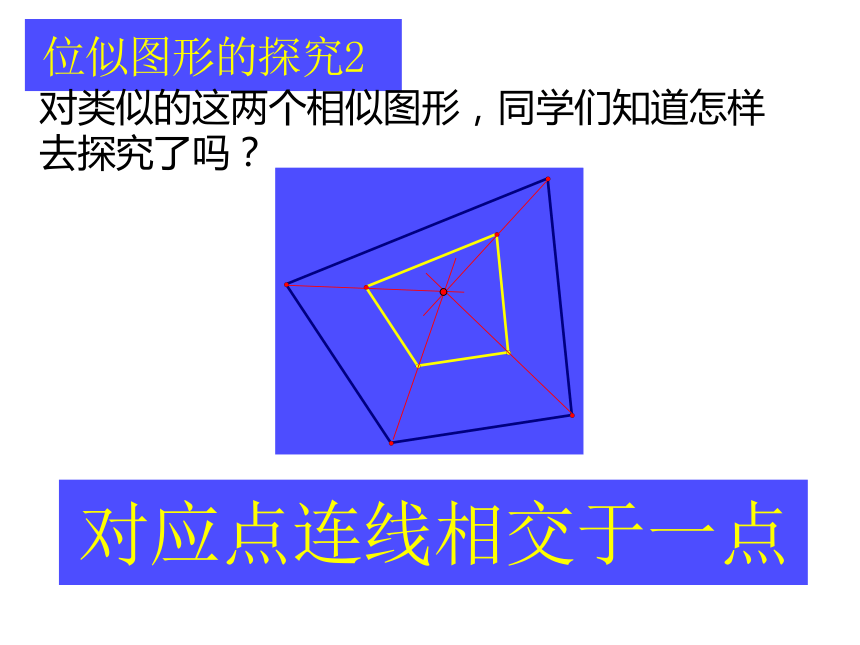
对类似的这两个相似图形,同学们知道怎样
去探究了吗?
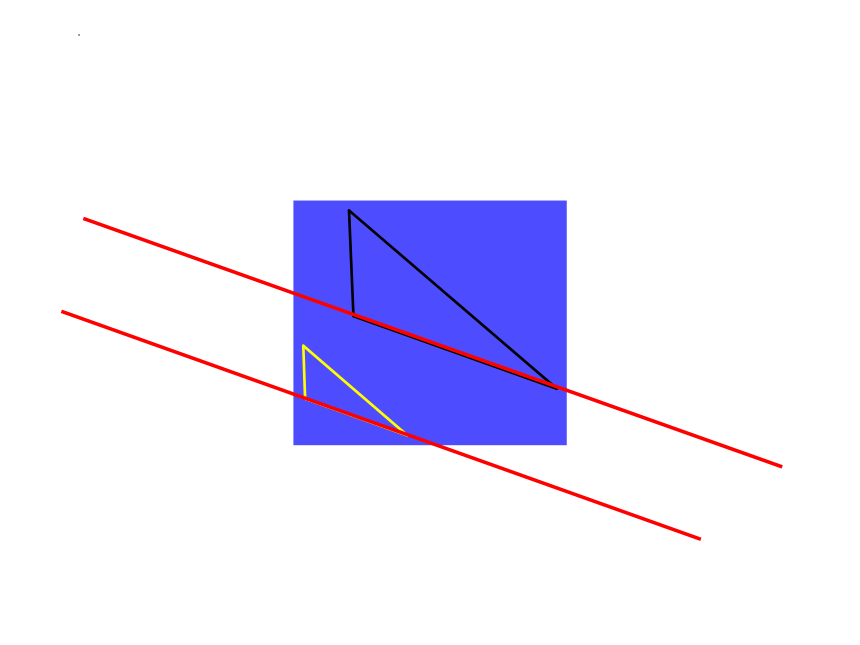
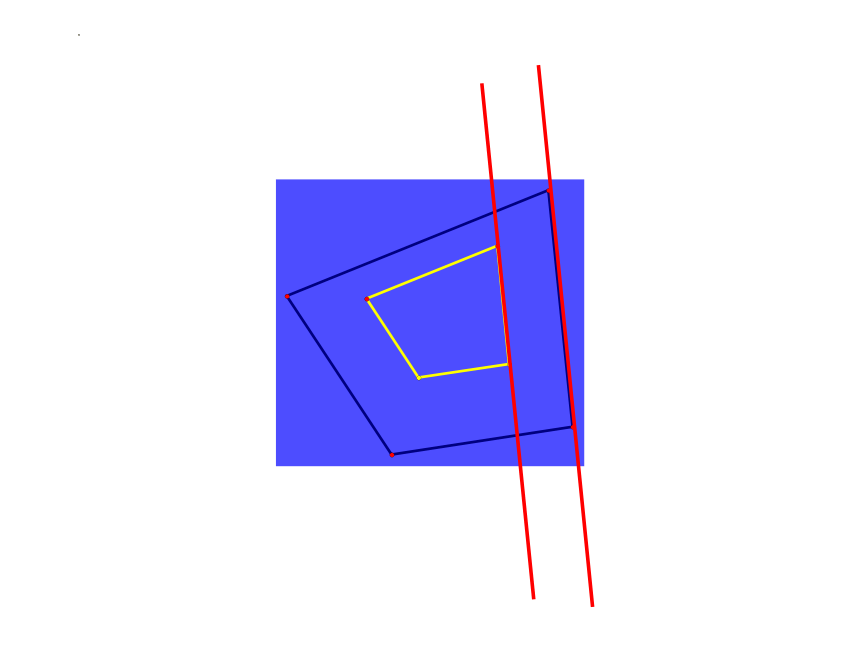
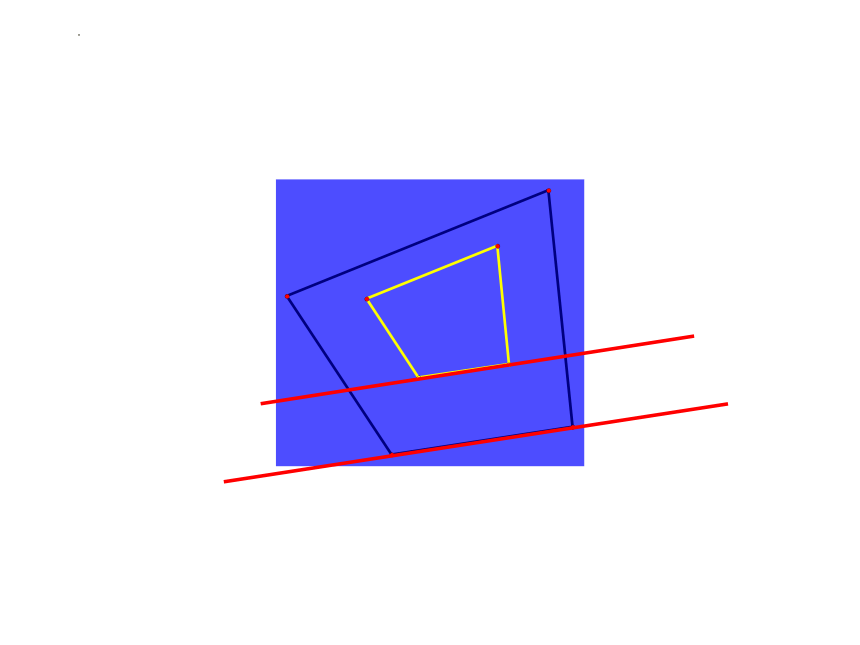
根据经验,我们从对应边的位置关系去探究。
再探究这两个相似图形,对同学们来说已经不是难事了,我们完全有能力自己去探究!
①
P
A
②
③
④
⑤
B
C
D
E
F
如果两个图形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行(或共线),像这样的两个图形叫做位似图形, 这个点叫做位似中心, 这时的相似比又称为位似比.
.
.
请说明位似图形和相似图形的联系与区别。
位似图形是一种特殊的相似图形,而相似图形不
一定构成位似关系。
1.两图形相似.
同时满足下面三个条件的两个
图形才叫做位似图形.三条件缺一不可.
显然,位似图形是相似图形的特殊情形,其相似比又叫做它们的位似比.
2.每组对应点所在直线都
经过同一点.
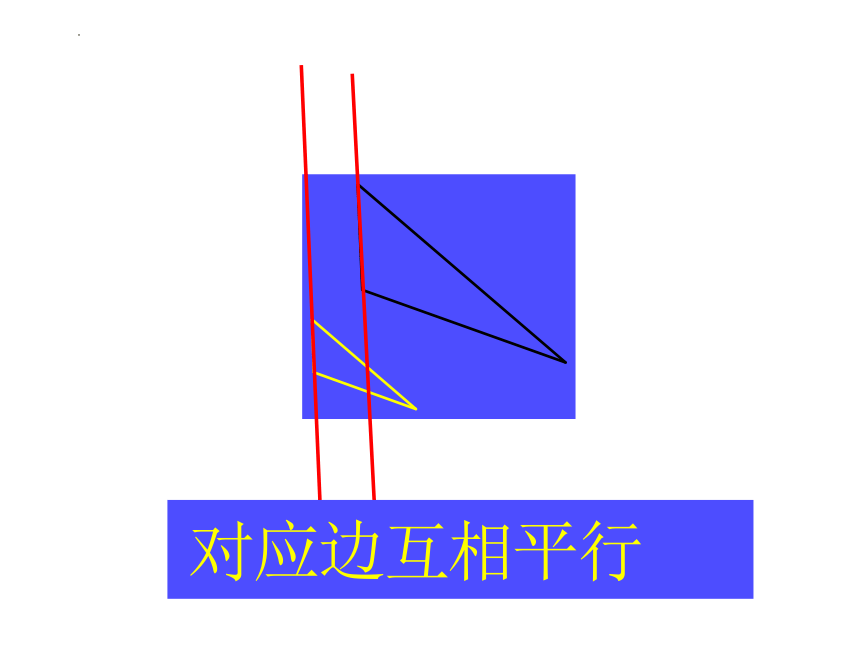
3. 对应边互相平行,
请指出下列图形那些是位似图形?
o
P
并指出位似图形图的位似中心
在图中任取一对对应点,度量这两个点到位似中心的距离,它们的比与位似比有什么关系
D
E
F
A
O
B
C
位似图形上任意一对对应点到位似中心的距离之比等于位似比
二.位似图形性质
A
H
G
F
E
D
C
B
O
L
K
在图中再试一试,还有类似的规律吗
位似图形的性质:位似图形上的任意一对对应点到位似中心的距离之比等于位似比
认一认:它们是位似图形吗?
4
3
6
4.5
2
5
你知道位似中心在哪儿吗 位似比是多少呢
2
4
3
6
2.5
5
这幅图的位似中心在哪儿 位似比是多少
若△ABC∽△DEF,那么,它们位似吗?位似中心在哪儿呢?
若△ADE∽△ABC呢?
若△ABC∽△EDC呢?
这种情况又如何呢?
做一做
你能得到的是正立放大的“像”、正立缩小的“像”、倒立缩小的“像”吗?
P
得到的是倒立放大的“像”
(1)将△ABC按比例缩小为原来的1/2:
O
A
B
C
如图,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F;
△DEF的三边就是△ABC相应三边的1/2.
△ABC与△DEF是位似图形吗
F
●
E
●
D
●
还有其他方法吗
利用位似把图形放大或缩小
在射线OA,OB,OC上分别取D,E,F,使OD=2OA, OE=2OB, OF=2OC,连接D,E,F,
(3)如果在射线AO,BO,CO上分别取点D,E,F使DO=OA,EO=OB,FO=OC,那么,结果又会怎样呢
D
E
F
A
O
B
C
D
E
F
A
O
B
C
还有其他方法吗
结果会得到一个与△ABC全等的△DEF,.即它们的位似比是1∶1.
(2)如何把三角形ABC放大为原来的2倍
如图,D,E分别AB,AC上的点.
(1)如果DE∥BC,那么 ADE和 ABC是位似图形吗?为什么?
A
B
C
D
E
解:(1) ADE和 ABC是位似图形.理由是:
DE∥BC,所以∠ADE和=∠B, ∠AED =∠C.所以 ADE∽ ABC.
又因为 点A是 ADE和 ABC的公共点,点D和点B是对应点,点E和点C是对应点,直线BD与CE交于点A,所以 ADE和 ABC是位似图形.
如图,D,E分别AB,AC上的点.
(1)如果DE∥BC,那么 ADE和 ABC是位似图形吗?为什么?
A
B
C
D
E
(2)如果 ADE和 ABC是位似图形,那么DE∥BC吗?为什么?
解:(2) DE∥BC.理由是:
ADE和 ABC是位似图形,
ADE∽ ABC
∠ADE=∠B
DE∥BC.
o
A
B
C
D
E
F
如图:△ABC与 △FED是位似图形说明为什么AB∥FE
如图,已知△ABC∽△DEF, 它们对应顶点的连线AD,BE,CF相交于点O,这两个三角形是不是位似三角形
0
B
E
C
F
A
D
练一练
位似图形:
如果两个图形不仅相似,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.
位似图形的性质:位似图形上的任意一对对应点到位似中心的距离之比等于位似比
位似图形应用:放大或缩小原图形;
小结 拓展
正向或反向
截取或延长
1.两图形相似.
同时满足下面三个条件的两个
图形才叫做位似图形.三条件缺一不可.
显然,位似图形是相似图形的特殊情形,其相似比又叫做它们的位似比.
2.每组对应点所在直线都
经过同一点.
3. 对应边互相平行,
小明所在的班参加献血宣传活动,他准备做一个如图
所示的红十字标志,你能将它扩大五倍吗?
作业
Good Bye!
再见
27.3位似(1)
位似图形
位似图形
位似图形
位似图形
在幻灯机上放映幻灯片时,把幻灯片上的图象放大到屏幕上
在照相馆里,摄影师通过照相机把实物的图象缩小在底片上
这样放大或缩小的图形,形状_____,大小______,所以它们_____.
相同
不同
相似
放映机
D
E
F
A
O
B
C
下列图形中有多边形相似吗 如果有,那么这种相似有什么特征
如何探究这两个相似图形之间的内在关系呢?
除对应点连线外,我们还可以怎样去探究?
对类似的这两个相似图形,同学们知道怎样
去探究了吗?
根据经验,我们从对应边的位置关系去探究。
再探究这两个相似图形,对同学们来说已经不是难事了,我们完全有能力自己去探究!
①
P
A
②
③
④
⑤
B
C
D
E
F
如果两个图形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行(或共线),像这样的两个图形叫做位似图形, 这个点叫做位似中心, 这时的相似比又称为位似比.
.
.
请说明位似图形和相似图形的联系与区别。
位似图形是一种特殊的相似图形,而相似图形不
一定构成位似关系。
1.两图形相似.
同时满足下面三个条件的两个
图形才叫做位似图形.三条件缺一不可.
显然,位似图形是相似图形的特殊情形,其相似比又叫做它们的位似比.
2.每组对应点所在直线都
经过同一点.
3. 对应边互相平行,
请指出下列图形那些是位似图形?
o
P
并指出位似图形图的位似中心
在图中任取一对对应点,度量这两个点到位似中心的距离,它们的比与位似比有什么关系
D
E
F
A
O
B
C
位似图形上任意一对对应点到位似中心的距离之比等于位似比
二.位似图形性质
A
H
G
F
E
D
C
B
O
L
K
在图中再试一试,还有类似的规律吗
位似图形的性质:位似图形上的任意一对对应点到位似中心的距离之比等于位似比
认一认:它们是位似图形吗?
4
3
6
4.5
2
5
你知道位似中心在哪儿吗 位似比是多少呢
2
4
3
6
2.5
5
这幅图的位似中心在哪儿 位似比是多少
若△ABC∽△DEF,那么,它们位似吗?位似中心在哪儿呢?
若△ADE∽△ABC呢?
若△ABC∽△EDC呢?
这种情况又如何呢?
做一做
你能得到的是正立放大的“像”、正立缩小的“像”、倒立缩小的“像”吗?
P
得到的是倒立放大的“像”
(1)将△ABC按比例缩小为原来的1/2:
O
A
B
C
如图,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F;
△DEF的三边就是△ABC相应三边的1/2.
△ABC与△DEF是位似图形吗
F
●
E
●
D
●
还有其他方法吗
利用位似把图形放大或缩小
在射线OA,OB,OC上分别取D,E,F,使OD=2OA, OE=2OB, OF=2OC,连接D,E,F,
(3)如果在射线AO,BO,CO上分别取点D,E,F使DO=OA,EO=OB,FO=OC,那么,结果又会怎样呢
D
E
F
A
O
B
C
D
E
F
A
O
B
C
还有其他方法吗
结果会得到一个与△ABC全等的△DEF,.即它们的位似比是1∶1.
(2)如何把三角形ABC放大为原来的2倍
如图,D,E分别AB,AC上的点.
(1)如果DE∥BC,那么 ADE和 ABC是位似图形吗?为什么?
A
B
C
D
E
解:(1) ADE和 ABC是位似图形.理由是:
DE∥BC,所以∠ADE和=∠B, ∠AED =∠C.所以 ADE∽ ABC.
又因为 点A是 ADE和 ABC的公共点,点D和点B是对应点,点E和点C是对应点,直线BD与CE交于点A,所以 ADE和 ABC是位似图形.
如图,D,E分别AB,AC上的点.
(1)如果DE∥BC,那么 ADE和 ABC是位似图形吗?为什么?
A
B
C
D
E
(2)如果 ADE和 ABC是位似图形,那么DE∥BC吗?为什么?
解:(2) DE∥BC.理由是:
ADE和 ABC是位似图形,
ADE∽ ABC
∠ADE=∠B
DE∥BC.
o
A
B
C
D
E
F
如图:△ABC与 △FED是位似图形说明为什么AB∥FE
如图,已知△ABC∽△DEF, 它们对应顶点的连线AD,BE,CF相交于点O,这两个三角形是不是位似三角形
0
B
E
C
F
A
D
练一练
位似图形:
如果两个图形不仅相似,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.
位似图形的性质:位似图形上的任意一对对应点到位似中心的距离之比等于位似比
位似图形应用:放大或缩小原图形;
小结 拓展
正向或反向
截取或延长
1.两图形相似.
同时满足下面三个条件的两个
图形才叫做位似图形.三条件缺一不可.
显然,位似图形是相似图形的特殊情形,其相似比又叫做它们的位似比.
2.每组对应点所在直线都
经过同一点.
3. 对应边互相平行,
小明所在的班参加献血宣传活动,他准备做一个如图
所示的红十字标志,你能将它扩大五倍吗?
作业
Good Bye!
再见
