北师大版七年级数学下册4.1 认识三角形 同步练习(含解析)
文档属性
| 名称 | 北师大版七年级数学下册4.1 认识三角形 同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 69.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 17:53:19 | ||
图片预览


文档简介
4.1 认识三角形 同步练习 北师大版七年级(下)
一.选择题(共10小题)
1.如果一个三角形的三个内角都不相等,那么最小角一定小于( )
A.60° B.59° C.45° D.30°
2.若三角形三个内角的度数之比为1:2:3,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
3.在△ABC中,已知∠A=∠B=∠C,则三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.形状无法确定
4.在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大12°,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
5.有下列长度的三条线段能构成三角形的是( )
A.1 cm、2 cm、3 cm B.1 cm、4 cm、2 cm
C.2 cm、3 cm、4 cm D.6 cm、2 cm、3 cm
6.已知一个三角形有两条边相等,一边长为4cm,另一边长为7cm,则这个三角形的周长为( )
A.15 cm B.18 cm
C.不能确定 D.15 cm或18 cm
7.如图,∠1=100°,∠C=70°,则∠A的大小是( )
A.10° B.20° C.30° D.80°
8.三角形的两边分别为a和b(a>b),则周长l的范围是( )
A.2a<l<3b B.2a<l<2(a+b)
C.2a+b<l<a+2b D.2b<l<2(a+6)
9.下列说法中错误的是( )
A.三角形三条角平分线都在三角形的内部
B.三角形三条中线都在三角形的内部
C.三角形三条高都在三角形的内部
D.三角形三条高至少有一条在三角形的内部
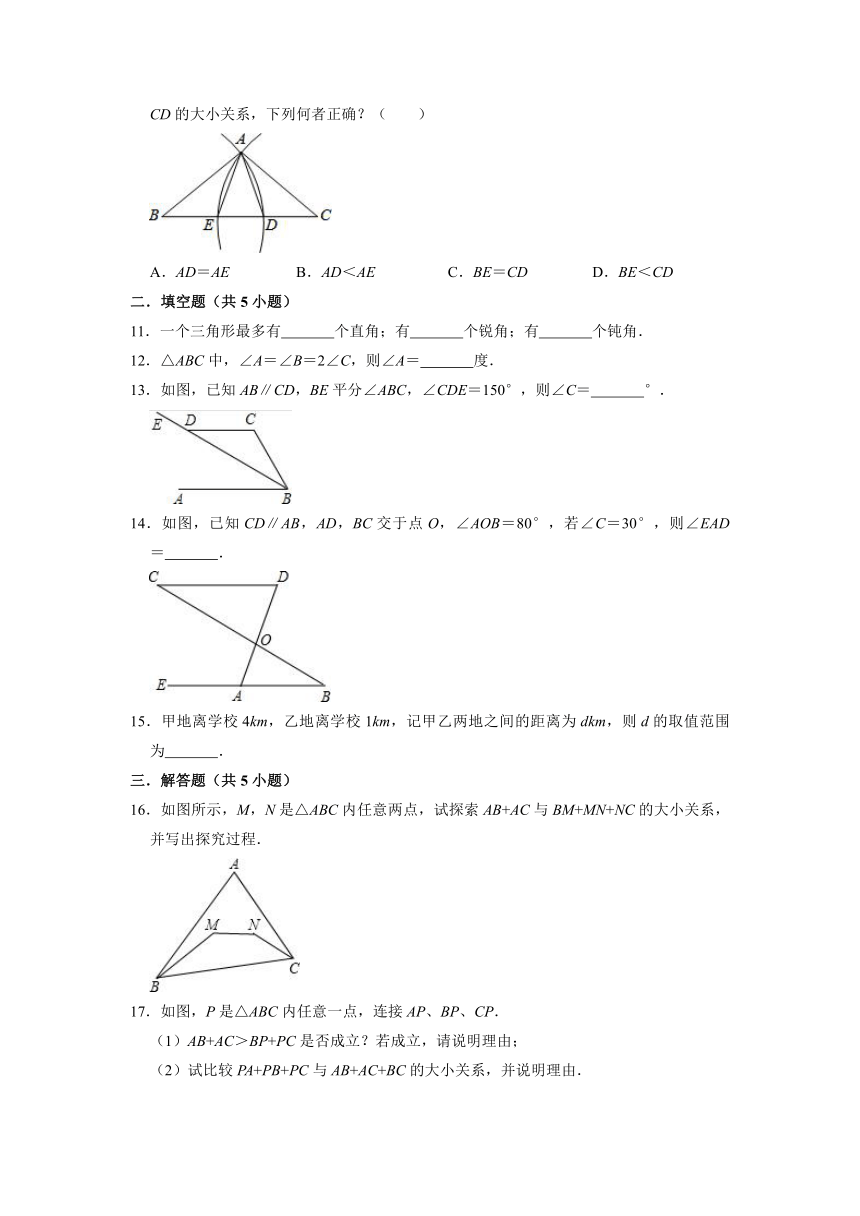
10.如图,有一△ABC,今以B为圆心,AB长为半径画弧,交BC于D点,以C为圆心,AC长为半径画弧,交BC于E点.若∠B=40°,∠C=36°,则关于AD、AE、BE、CD的大小关系,下列何者正确?( )
A.AD=AE B.AD<AE C.BE=CD D.BE<CD
二.填空题(共5小题)
11.一个三角形最多有 个直角;有 个锐角;有 个钝角.
12.△ABC中,∠A=∠B=2∠C,则∠A= 度.
13.如图,已知AB∥CD,BE平分∠ABC,∠CDE=150°,则∠C= °.
14.如图,已知CD∥AB,AD,BC交于点O,∠AOB=80°,若∠C=30°,则∠EAD= .
15.甲地离学校4km,乙地离学校1km,记甲乙两地之间的距离为dkm,则d的取值范围为 .
三.解答题(共5小题)
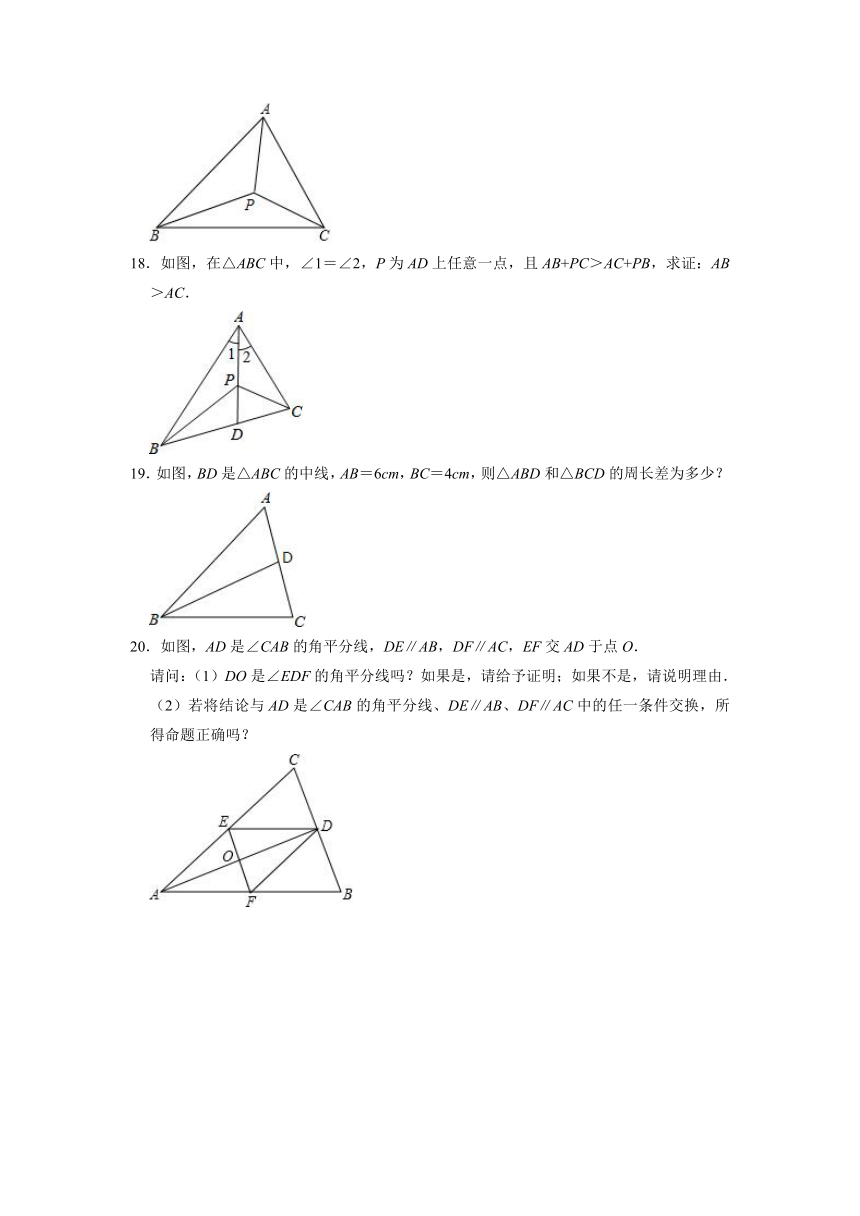
16.如图所示,M,N是△ABC内任意两点,试探索AB+AC与BM+MN+NC的大小关系,并写出探究过程.
17.如图,P是△ABC内任意一点,连接AP、BP、CP.
(1)AB+AC>BP+PC是否成立?若成立,请说明理由;
(2)试比较PA+PB+PC与AB+AC+BC的大小关系,并说明理由.
18.如图,在△ABC中,∠1=∠2,P为AD上任意一点,且AB+PC>AC+PB,求证:AB>AC.
19.如图,BD是△ABC的中线,AB=6cm,BC=4cm,则△ABD和△BCD的周长差为多少?
20.如图,AD是∠CAB的角平分线,DE∥AB,DF∥AC,EF交AD于点O.
请问:(1)DO是∠EDF的角平分线吗?如果是,请给予证明;如果不是,请说明理由.
(2)若将结论与AD是∠CAB的角平分线、DE∥AB、DF∥AC中的任一条件交换,所得命题正确吗?
4.1 认识三角形 同步练习 2023年北师大版七年级(下)
参考答案与试题解析
一.选择题(共10小题)
1. 解:假设,最小角度大于或等于60°,则另外两个角一定也大于60°,
那么此三角形内角和大于180°,
故假设不成立,
所以此三角形的最小角一定要小于60°.
故选:A.
2. 解:设一份为k°,则三个内角的度数分别为k°,2k°,3k°,
根据三角形内角和定理,可知k°+2k°+3k°=180°,
得k°=30°,
那么三角形三个内角的度数分别是30°,60°和90°.
故选:B.
3. 解:∵∠A=∠B=∠C,
∴∠B=2∠A,∠C=3∠A,
又∵A+∠B+∠C=180°,
∴∠A+2∠A+3∠A=180°,
解得:∠A=30°,
∴∠C=90°.
即该三角形是直角三角形.
故选:B.
4. 解:设∠B为x,则∠A=2x,∠C=3x+12,
由题意得:x+2x+3x+12=180°,
解得:x=28°,2x=56°,3x+12=96°,
即三角形为钝角三角形.
故选:C.
5. 解:根据三角形的三边关系,得
A、1+2=3,不能组成三角形,故此选项错误;
B、1+2<4,不能组成三角形,故此选项错误;
C、2+3>4,能够组成三角形,故此选项正确;
D、2+3<6,不能组成三角形,故此选项错误.
故选:C.
6. 解:当相等的两边是4cm时,另一边长为7cm,则三角形的周长是4×2+7=15cm,
当相等的两边是7cm时,则三角形的周长是4+7×2=18cm,
故选:D.
7. 解:∵∠1=100°,∠C=70°,
∴∠A=∠1﹣∠C=100°﹣70°=30°.
故选:C.
8. 解:假设第三边为c,
由三角形三边关系定理得:a﹣b<c<a+b,
∴这个三角形的周长C的取值范围是:a+b+a﹣b<l<a+b+a+b=2(a+b),
∴2a<l<2(a+b),
故选:B.
9. 解:A、三角形三条角平分线都在三角形的内部,故正确;
B、三角形三条中线都在三角形的内部,故正确;
C、直角三角形有两条高就是直角三角形的边,一条在内部,钝角三角形有两条高在外部,一条在内部,故错误.
D、三角形三条高至少有一条在三角形的内部,故正确.
故选:C.
10. 解:∵∠C<∠B,
∴AB<AC,
∵AB=BDAC=EC
∴BE+ED<ED+CD,
∴BE<CD.
故选:D.
二.填空题(共5小题)
11. 解:如果一个三角形中出现2个或3个钝角,那么三角形的内角和就大于180°,不符合三角形内角和是180°;
如果一个三角形中出现2个或3个直角,再加上第三个角,那么三角形的内角和就大于180°,也不符合三角形内角和是180°;
所以,三角形中最多有一个钝角或直角,最少有两个锐角,一个三角形中最多有3个锐角,如锐角三角形.
故答案为:1,3,1.
12. 解:∵∠A+∠B+∠C=180°,∠A=∠B=2∠C,
∴5∠C=180°,即∠C=36°.
则∠A=72°.
13. 解:∵∠CDE=150°,
∴∠CDB=180﹣∠CDE=30°,
又∵AB∥CD,
∴∠ABD=∠CDB=30°;
∵BE平分∠ABC,
∴∠ABC=60°,
∴∠C=180°﹣60°=120°.
故答案为:120.
14. 解:∵CD∥AB,
∴∠B=∠C=30°,
∵∠AOB=80°,
∴∠EAO=∠AOB+∠B=80°+30°=110°.
故答案为:110°.
15. 解:(1)甲乙都在学校同侧,则d≥4﹣1=3;
(2)甲乙在学校两侧,则d≤4+1=5;
则d的取值范围为:3≤d≤5.
三.解答题(共5小题)
16. 解:AB+AC>BM+MN+NC.
理由:延长BM交AC于D,延长MN交AC于F,
∴AB+AD>BM+MD①,
DM+DF>MN+NF②,
NF+CF>CN③,
∴①+②+③得,AB+AC>BM+MN+NC.
17. 解:(1)成立.
理由:延长BP交AC于点D,
在△ABD中,PB+PD<AB+AD①,
在△PCD中,PC<PD+CD②,
①+②得PB+PD+PC<AB+AD+PD+CD,
即PB+PC<AB+AC,
即:AB+AC>PB+PC.
(2)结论:PA+PB+PC<AB+AC+BC.
根据第一问的结论有 PB+PC<AB+AC,
PA+PB<CA+CB,
PA+PC<BA+BC,
∴2PA+2PB+2PC<2AB+2AC+2BC,
∴PA+PB+PC<AB+AC+BC.
18. 证明:假设AC>AB,在AB上截取AE,使AE=AC,连接PE,
在△AEP和△ACP中,
,
∴△AEP≌△ACP(SAS),
∴PE=PC,
∵AB+PC>AC+PB,
∴AC﹣AB>PC﹣PB,
BE<PE﹣PB,
在△PBE中,BE>PE﹣PB,
假设不成立;
若AB=AC,
在△ABP和△ACP中,
,
∴△ABP≌△ACP(SAS),
∴PB=PC,
∴AB+PC=AC+PB,
与已知矛盾,
综上所述AB>AC.
19. 解:∵BD是△ABC的中线,
∴AD=CD,
∴△ABD和△BCD的周长差=(AB+AD+BD)﹣(BC+CD+BD),
=AB+AD+BD﹣BC﹣CD﹣BD,
=AB﹣BC,
∵AB=6cm,BC=4cm,
∴△ABD和△BCD的周长差=6﹣4=2cm.
答:△ABD和△BCD的周长差为2cm.
20. (1)DO是∠EDF的角平分线,
证明:∵DE∥AB,DF∥AC,
∴四边形AFDE是平行四边形,
∵AD是∠CAB的角平分线,
∴∠EAD=∠FAD,
∵DE∥AB,
∴∠EDA=∠FAD,
∴∠EAD=EDA,
∴AE=DE,
∴平行四边形AFDE是菱形,
∴DO是∠EDF的角平分线.
(2)解:正确.
①如和AD是∠CAB的角平分线交换,正确,理由与(1)证明过程相似;
②如和DE∥AB交换,
理由是:∵DF∥AC,
∴∠FDA=∠EAD,
∵AD是∠CAB的角平分线,DO是∠EDF的角平分线,
∴∠EAD=∠FAD,∠EDA=∠FDA,
∴∠EAF=∠EDF,
∵AE∥DF,
∴∠AEF=∠DFE,
∵∠EDF+∠EFD+∠DEF=180°,∠EAF+∠AEF+∠AFE=180°,
∴∠DEF=∠AFE,
∴DE∥AB,正确.
③如和AE∥DF交换,正确理由与②类似.
答:若将结论与AD是∠CAB的角平分线、DE∥AB、DF∥AC中的任一条件交换,所得命题正确.
一.选择题(共10小题)
1.如果一个三角形的三个内角都不相等,那么最小角一定小于( )
A.60° B.59° C.45° D.30°
2.若三角形三个内角的度数之比为1:2:3,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
3.在△ABC中,已知∠A=∠B=∠C,则三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.形状无法确定
4.在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大12°,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
5.有下列长度的三条线段能构成三角形的是( )
A.1 cm、2 cm、3 cm B.1 cm、4 cm、2 cm
C.2 cm、3 cm、4 cm D.6 cm、2 cm、3 cm
6.已知一个三角形有两条边相等,一边长为4cm,另一边长为7cm,则这个三角形的周长为( )
A.15 cm B.18 cm
C.不能确定 D.15 cm或18 cm
7.如图,∠1=100°,∠C=70°,则∠A的大小是( )
A.10° B.20° C.30° D.80°
8.三角形的两边分别为a和b(a>b),则周长l的范围是( )
A.2a<l<3b B.2a<l<2(a+b)
C.2a+b<l<a+2b D.2b<l<2(a+6)
9.下列说法中错误的是( )
A.三角形三条角平分线都在三角形的内部
B.三角形三条中线都在三角形的内部
C.三角形三条高都在三角形的内部
D.三角形三条高至少有一条在三角形的内部
10.如图,有一△ABC,今以B为圆心,AB长为半径画弧,交BC于D点,以C为圆心,AC长为半径画弧,交BC于E点.若∠B=40°,∠C=36°,则关于AD、AE、BE、CD的大小关系,下列何者正确?( )
A.AD=AE B.AD<AE C.BE=CD D.BE<CD
二.填空题(共5小题)
11.一个三角形最多有 个直角;有 个锐角;有 个钝角.
12.△ABC中,∠A=∠B=2∠C,则∠A= 度.
13.如图,已知AB∥CD,BE平分∠ABC,∠CDE=150°,则∠C= °.
14.如图,已知CD∥AB,AD,BC交于点O,∠AOB=80°,若∠C=30°,则∠EAD= .
15.甲地离学校4km,乙地离学校1km,记甲乙两地之间的距离为dkm,则d的取值范围为 .
三.解答题(共5小题)
16.如图所示,M,N是△ABC内任意两点,试探索AB+AC与BM+MN+NC的大小关系,并写出探究过程.
17.如图,P是△ABC内任意一点,连接AP、BP、CP.
(1)AB+AC>BP+PC是否成立?若成立,请说明理由;
(2)试比较PA+PB+PC与AB+AC+BC的大小关系,并说明理由.
18.如图,在△ABC中,∠1=∠2,P为AD上任意一点,且AB+PC>AC+PB,求证:AB>AC.
19.如图,BD是△ABC的中线,AB=6cm,BC=4cm,则△ABD和△BCD的周长差为多少?
20.如图,AD是∠CAB的角平分线,DE∥AB,DF∥AC,EF交AD于点O.
请问:(1)DO是∠EDF的角平分线吗?如果是,请给予证明;如果不是,请说明理由.
(2)若将结论与AD是∠CAB的角平分线、DE∥AB、DF∥AC中的任一条件交换,所得命题正确吗?
4.1 认识三角形 同步练习 2023年北师大版七年级(下)
参考答案与试题解析
一.选择题(共10小题)
1. 解:假设,最小角度大于或等于60°,则另外两个角一定也大于60°,
那么此三角形内角和大于180°,
故假设不成立,
所以此三角形的最小角一定要小于60°.
故选:A.
2. 解:设一份为k°,则三个内角的度数分别为k°,2k°,3k°,
根据三角形内角和定理,可知k°+2k°+3k°=180°,
得k°=30°,
那么三角形三个内角的度数分别是30°,60°和90°.
故选:B.
3. 解:∵∠A=∠B=∠C,
∴∠B=2∠A,∠C=3∠A,
又∵A+∠B+∠C=180°,
∴∠A+2∠A+3∠A=180°,
解得:∠A=30°,
∴∠C=90°.
即该三角形是直角三角形.
故选:B.
4. 解:设∠B为x,则∠A=2x,∠C=3x+12,
由题意得:x+2x+3x+12=180°,
解得:x=28°,2x=56°,3x+12=96°,
即三角形为钝角三角形.
故选:C.
5. 解:根据三角形的三边关系,得
A、1+2=3,不能组成三角形,故此选项错误;
B、1+2<4,不能组成三角形,故此选项错误;
C、2+3>4,能够组成三角形,故此选项正确;
D、2+3<6,不能组成三角形,故此选项错误.
故选:C.
6. 解:当相等的两边是4cm时,另一边长为7cm,则三角形的周长是4×2+7=15cm,
当相等的两边是7cm时,则三角形的周长是4+7×2=18cm,
故选:D.
7. 解:∵∠1=100°,∠C=70°,
∴∠A=∠1﹣∠C=100°﹣70°=30°.
故选:C.
8. 解:假设第三边为c,
由三角形三边关系定理得:a﹣b<c<a+b,
∴这个三角形的周长C的取值范围是:a+b+a﹣b<l<a+b+a+b=2(a+b),
∴2a<l<2(a+b),
故选:B.
9. 解:A、三角形三条角平分线都在三角形的内部,故正确;
B、三角形三条中线都在三角形的内部,故正确;
C、直角三角形有两条高就是直角三角形的边,一条在内部,钝角三角形有两条高在外部,一条在内部,故错误.
D、三角形三条高至少有一条在三角形的内部,故正确.
故选:C.
10. 解:∵∠C<∠B,
∴AB<AC,
∵AB=BDAC=EC
∴BE+ED<ED+CD,
∴BE<CD.
故选:D.
二.填空题(共5小题)
11. 解:如果一个三角形中出现2个或3个钝角,那么三角形的内角和就大于180°,不符合三角形内角和是180°;
如果一个三角形中出现2个或3个直角,再加上第三个角,那么三角形的内角和就大于180°,也不符合三角形内角和是180°;
所以,三角形中最多有一个钝角或直角,最少有两个锐角,一个三角形中最多有3个锐角,如锐角三角形.
故答案为:1,3,1.
12. 解:∵∠A+∠B+∠C=180°,∠A=∠B=2∠C,
∴5∠C=180°,即∠C=36°.
则∠A=72°.
13. 解:∵∠CDE=150°,
∴∠CDB=180﹣∠CDE=30°,
又∵AB∥CD,
∴∠ABD=∠CDB=30°;
∵BE平分∠ABC,
∴∠ABC=60°,
∴∠C=180°﹣60°=120°.
故答案为:120.
14. 解:∵CD∥AB,
∴∠B=∠C=30°,
∵∠AOB=80°,
∴∠EAO=∠AOB+∠B=80°+30°=110°.
故答案为:110°.
15. 解:(1)甲乙都在学校同侧,则d≥4﹣1=3;
(2)甲乙在学校两侧,则d≤4+1=5;
则d的取值范围为:3≤d≤5.
三.解答题(共5小题)
16. 解:AB+AC>BM+MN+NC.
理由:延长BM交AC于D,延长MN交AC于F,
∴AB+AD>BM+MD①,
DM+DF>MN+NF②,
NF+CF>CN③,
∴①+②+③得,AB+AC>BM+MN+NC.
17. 解:(1)成立.
理由:延长BP交AC于点D,
在△ABD中,PB+PD<AB+AD①,
在△PCD中,PC<PD+CD②,
①+②得PB+PD+PC<AB+AD+PD+CD,
即PB+PC<AB+AC,
即:AB+AC>PB+PC.
(2)结论:PA+PB+PC<AB+AC+BC.
根据第一问的结论有 PB+PC<AB+AC,
PA+PB<CA+CB,
PA+PC<BA+BC,
∴2PA+2PB+2PC<2AB+2AC+2BC,
∴PA+PB+PC<AB+AC+BC.
18. 证明:假设AC>AB,在AB上截取AE,使AE=AC,连接PE,
在△AEP和△ACP中,
,
∴△AEP≌△ACP(SAS),
∴PE=PC,
∵AB+PC>AC+PB,
∴AC﹣AB>PC﹣PB,
BE<PE﹣PB,
在△PBE中,BE>PE﹣PB,
假设不成立;
若AB=AC,
在△ABP和△ACP中,
,
∴△ABP≌△ACP(SAS),
∴PB=PC,
∴AB+PC=AC+PB,
与已知矛盾,
综上所述AB>AC.
19. 解:∵BD是△ABC的中线,
∴AD=CD,
∴△ABD和△BCD的周长差=(AB+AD+BD)﹣(BC+CD+BD),
=AB+AD+BD﹣BC﹣CD﹣BD,
=AB﹣BC,
∵AB=6cm,BC=4cm,
∴△ABD和△BCD的周长差=6﹣4=2cm.
答:△ABD和△BCD的周长差为2cm.
20. (1)DO是∠EDF的角平分线,
证明:∵DE∥AB,DF∥AC,
∴四边形AFDE是平行四边形,
∵AD是∠CAB的角平分线,
∴∠EAD=∠FAD,
∵DE∥AB,
∴∠EDA=∠FAD,
∴∠EAD=EDA,
∴AE=DE,
∴平行四边形AFDE是菱形,
∴DO是∠EDF的角平分线.
(2)解:正确.
①如和AD是∠CAB的角平分线交换,正确,理由与(1)证明过程相似;
②如和DE∥AB交换,
理由是:∵DF∥AC,
∴∠FDA=∠EAD,
∵AD是∠CAB的角平分线,DO是∠EDF的角平分线,
∴∠EAD=∠FAD,∠EDA=∠FDA,
∴∠EAF=∠EDF,
∵AE∥DF,
∴∠AEF=∠DFE,
∵∠EDF+∠EFD+∠DEF=180°,∠EAF+∠AEF+∠AFE=180°,
∴∠DEF=∠AFE,
∴DE∥AB,正确.
③如和AE∥DF交换,正确理由与②类似.
答:若将结论与AD是∠CAB的角平分线、DE∥AB、DF∥AC中的任一条件交换,所得命题正确.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
