2022-2023学年人教版七年级数学下册8.2 消元——解二元一次方程组课件(共36张PPT)
文档属性
| 名称 | 2022-2023学年人教版七年级数学下册8.2 消元——解二元一次方程组课件(共36张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 18:27:00 | ||
图片预览











文档简介
(共36张PPT)
8.2.2 消元——解二元一次方程组
(加减消元法)
主要步骤:
基本思路:
4、写解
3、求解
2、代入
把变形后的方程代入到另一个方程中,消去一个元
分别求出两个未知数的值
写出方程组的解
1、变形
用含有一个未知数的代数式表示另一个未知数,写成y=ax+b或x=ay+b
消元: 二元
1、解二元一次方程组的基本思路是什么?
2、用代入法解方程的步骤是什么?
一元
复习:
解法一:设胜x场,负y场,则有
x+y=10①
2x+y=16②
篮球联赛中,每场都要分出胜负,每队胜一场得2分,负一场得1分,某队为了争取较好的名次,想在全部的10场比赛中得到16分,那么这个队胜负应该分别是多少?
新课导入
x+y=10
2x+y=16
这两个方程中未知数y的系数相同,
①
②
②-①可消去未知数y得
把x=6代入①,得 y=4.
①-②也能消去
未知数y,求得
x吗
像这样,通过对方程组中的两个方程进行加或减的运算就
可以消去一个未知数,得到一个一元一次方程,这种方法叫做
加减消元法,简称加减法.
x=6
(②-①等式性质)
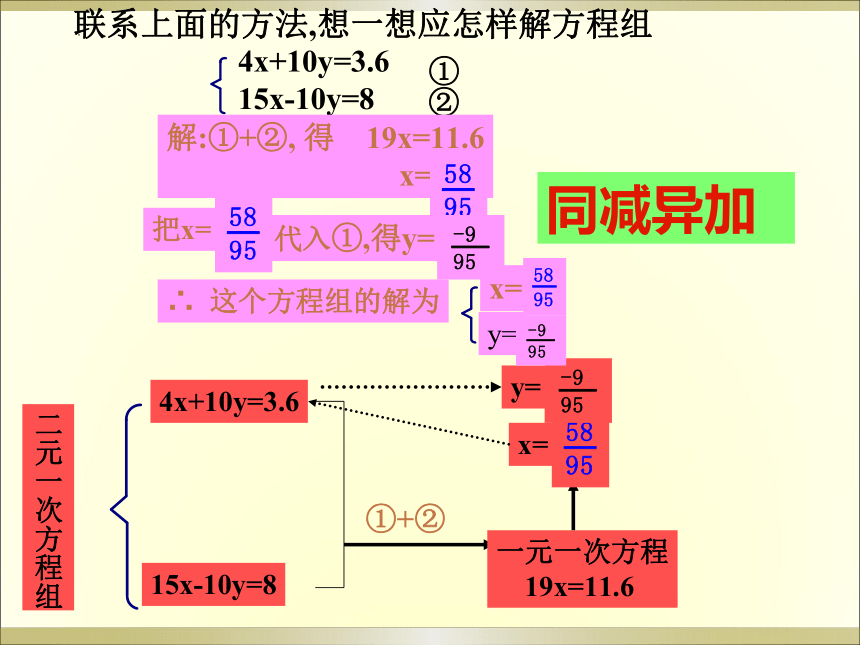
联系上面的方法,想一想应怎样解方程组
4x+10y=3.6
15x-10y=8
①②
解:①+②, 得 19x=11.6
x=
二元一次方程组
4x+10y=3.6
15x-10y=8
一元一次方程
19x=11.6
x=
y=
把x=
代入①,得y=
∴ 这个方程组的解为
x=
y=
①+②
同减异加
归纳:
我们发现,如果二元一次方程组的两个方程中
某个未知数的系数相同或互为相反数,就可以直接用
加减法显得非常简便.
例1.用加减法解下列方程组:
(1)
4x+y=2
4x-3y=-6
①②
解: (1)①-②, 得
4y=8
y=2
把y=2代入方程①,得
x=0
3x + 7y = 27 ①
4x - 7y =-13 ②
(2)
解:
① + ②,得
7x = 14
把 x = 2 代入①,得
3 ×2 + 7y = 27
y= 3
所以原方程组的解是
x = 2
y = 3
所以原方程组的解是
x = 0
y = 2
(1) ①×2-②, 得
4x=5
x=1.25
把x=1.25代入②,得
y=-2.375
3x+2y=-1
2x+4y=-7
(1)
所以,原方程组的解为
x = 1.25
y = -2.375
① ②
例2:
(3)
7x+3y=36
2x+9y=51
系数的绝对值成倍数关系:
归纳:当两个方程中某个未知数的
系数成倍数关系时,我们也可以用加
减法,只不过在加或减之前,可先将一
个方程变形成与另一个方程中相同
未知数的系数相同,这样就可以达到
消元的目的.
① ②
看一看下面这个例子,我们又该如何解决呢
3x+4y=16
5x-6y=33
能用加减法做吗 怎么做呢 试试看!
解:① × 3 ,得:9x+12y=48 ③
②×2,得:10x-12y=66 ④
③十④,得:19x= 11
x=6
把x=6代入①得 3x6+4y=16
y=-1/2
所以原方程组的解为 x=6
y=-1/2
例3:
例4: 用加减法解方程组
4x+5y=23 ①
5x-2y=4 ②
解:①×2,得 8x+10y=46 ③
②×5,得 25x-10y=20 ④
③+④,得 33x=66 x=2
把x=2代入②,得 5×2-2y=4, y=3
所以这个方程组的解是
x=2
y=3
(1)
(2)
加减法归纳:
用加减法解同一个未知数的系数绝对值不相等,且不成整数倍的二元一次方程组时,把一个(或两个)方程的两边乘以适当的数,使两个方程中某一未知数的系数绝对值相等,从而化为第一类型方程组求解.
解:原方程组变形为
①-②,得:2y=2 y=1
把y=1代入①,得x=2
例5 用加减法解方程组
2(2x+1)=15-5y
3(y+1)=14-4x
4x+5y=13 ①
4x+3y=11 ②
x=2
y=1
所以原方程组的解是
解:由①×6,得
3x+2y=9 ③
由②×15,得
5x-3y=15 ④
例6 用加减法解方程组
②
①
③④组成一个新的方程组:
3x+2y=9 ③
5x-3y=15 ④
③×3,得 9x+6y=27 ⑤
④×2,得 10x-6y=30 ⑥
⑤+⑥,得 19x= 57 x=3
把x= 3代入③,得
3×3+2y=9
y=0
所以原方程组的解是
x=3
y=0
对于较复杂的二元一次方程组,应先化简(去分母,去括号, 合并同类项等),通常要把每个方程整理成含未知数的项在方程的左边,常数项在方程的右边的形式,再作加减消元的考虑。
注意:
复杂方程先化简
基本思路:
主要步骤:
加减消元:
二元
一元
加减消元法解方程组基本思路是什么?主要步骤有哪些?
处理系数
同一个未知数的系
数变成相同或相反的数
代入
求值2
写解
写出方程组的解
加/减
求值1
解方程组:
解:原方程组可化为:
2x+3y=4 ③
2x - y=8 ④
由③-④得: y= -1
所以原方程组
的解是
把y= -1代入② ,
解得:
②
①
方法1:
由 ④得: y= 2x-8
⑤
把⑤代入③ ,得:
2x+3 (2x-8) =4
x=7/2
把x=7/2代入⑤得
y=-1
方法2:
主要步骤:
基本思路:
写解
求解
加减
二元变一元
加减消元:
消去一个元
求出两个未知数的值
写出方程组的解
加减消元法解方程组基本思路和主要步骤:
变形
同一个未知数的系数相同或互为相反数
每个二元一次方程组均可采用代入法和加减法求解,但在解题中
要根据方程组的特点灵活选用最恰当的方法,使计算过程更简便。
当化简后的方程组存在一个方程的某个未知数系数的绝对值是1或
有一个方程的常数项是0时,用代入法;当两个方程中某个未知数
的绝对值相等或整数倍时,用加减法。
例 7: 2台大收割机和5台小收割机工作2小时收割小麦3.6公顷,3台大收割机和2台小收割机工作5小时收割小麦8公顷,1台大收割机和1台小收割机1小时各收割小麦多少公顷?
解:设1台大收割机和1台小收割机1小时各收割小麦x公顷和y公顷
化简,得:
①
②
②-①,得: 11x=4.4,
解得 x=0.4
把x=0.4代入①中,得:y=0.2
所以原方程组的解是
答:1台大收割机和1台小收割机1小时各收割小麦0.4公顷和0.2公顷。
例8: 两个完全相同的纸杯中盛有相同重量的水,现将第一个纸杯中的若干重量的水倒入第二个纸杯中,称得第一个纸杯重50克,第二个纸杯重90克(纸杯本身的重量忽略不计),问原来纸杯中各盛有多少克水?从第一个纸杯中倒了多少克水到第二个纸杯中?
解:设原来纸杯中盛有x克水,从第一个纸杯中倒入第二个纸杯中的水为y克,根据题意,得
x-y=50 ①
x+y=90 ②
①+②得:(x-y)+(x+y)=50+90,
则有 2x=50+90 所以 x=70
或者:
②-①得 :(x+y) -(x-y)=90-50,
则有 2y=40 所以 y=20
x-y=50 ①
x+y=90 ②
上述方程的另一种解法是:
例9 已知方程组
与方程组
的解相同,求a,b的值.
ax-by=4
ax+by=2
4x+3y=11
4x-5y=3
解方程组
得
解:
4x+3y=11
4x-5y=3
把x=2,y=1代入 得,
ax-by=4
ax+by=2
x=2
y=1
2a-b=4
2a+b=2
解得
a=1.5
b=-1
例10 解关于x,y的方程组
4x+3ky+1=0 ①
6y-4x=1 ②
解:①+②得(3k+6)y=0
即(2+k)y=0
(1)当k≠-2时,y=0
(2)当k=-2时,则k+2=0,(2+k)y=0恒成立
原方程组有无数组解.
把y=0代入②,得 -4x=1
y=0
例11 已知4|5x+3y-23| +5(x+4y-8)2 = 0 ,求x-y的值.
解:由题知,
5x+3y-23=0 ①
x+4y-8=0 ②
解这个方程组,得
x=4
y=1
所以 x-y=4-1=3
例12 已知4x3a+b-3 +3y2a-b=2,是关于x、y的二元一次方程,试求a、b的值.
解:根据题意:得
3a+b-3=1
2a-b=1
解,得
a=1
b=1
解:由已知得
3x-2y- 8z=0 ①
2x+y-10z=0 ②
例13 已知:3x-2y-8z=0,2x+y-10z=0,且x,y,z均不为零,求 的值.
解得
x=4z
y=2z
把x=4z,y=2z代入所求代数式,解得
例13 当x = 2与x = -3时,代数式2x2+ax-b的值都是9,求a, b 的值.
解:把x=2,x=-3代入2x2+ax-b,得
8+2a-b=9
18-3a-b=9
即
2a-b=1
3a+b=9
解,得
a=2
b=3
例14 a 为何值时,方程组 的解互为相反数,并求它的值.
2x-7y=9a
3x+4y=a-6
解:若方程组的解互为相反数,则有y=-x,将y=-x代入原方程组,得
2x+7x=9a
3x-4x=a-6
解,得
x=3
a=3
当a=3时,原方程组中的解互为相反数,
即
x=3
y=-3
例15 m , n 为何值时,5x4m-ny3m+2n与3x5y6m是同类项.
解:根据同类项的定义,有
4m-n=5
3m+2n=6m
解,得
m=2
n=3
1.代入消元法解二元一次方程组
对于用代入法解未知数系数的绝对值不是1的二元一次方程组,解题时应选择未知数的系数绝对值比较小的一个方程进行变形,这样运算简便.
课堂小结
用加减法解二元一次方程组的思想:“二元”消元转化为“一元”.条件:某一未知数系数绝对值相等.
2.用加减消元法解二元一次方程组
2.若(x-2y-3)2+(2x-y-3)2=0, 则x、y的
值是x=___,y=______.
1
-1
1.二元一次方程组 的解是________.
4x-y=5
5x+2y=10
x=0
y=-5
3.已知│x+y-5│+(2x-3y+10)2=0,则
x=____,y=____.
1
4
随堂练习
4.己知: ,则方程组
的解是___________.
x=2,y=3
5.已知(3m+2n-16)2与|3m-n-1|互为相反数,
则m+2n=_______.
12
6.若方程 (a2-9)x2+(2-4a)x+(a+4)y+
3a-5=0 是二元一次方程,则a的值为__.
±3
7.已知5a3xb2x-y和-9a8-yb7是同类项,则2xy=____.
-6
2
3
8.若方程组 与 方程组
同解,则 m=______,n=______.
9.下列方程组中,
x=_____,y=______.
4
2
10.已知方程组 ,且x+y=2,
则m2-2m+5的值是____.
11.当m≠__时,方程组 有一组解.
8
12.已知方程组 ,且y=3x,则m=___.
1
13.己知 ,则
的值是______.
2
14. 己知 ,则 的值是
_______.
2
15.如果二元一次方程组
ax-by=1,
3ax+2by=23
的解是
x=5
y=4.
求a-b的值.
1、若方程组 的解满足
2x-5y=-1,则m 为多少?
2、若(3x+2y-5)2+|5x+3y-8|=0
求x2+y-1的值。
x+y=8m
x-y=2m
8.2.2 消元——解二元一次方程组
(加减消元法)
主要步骤:
基本思路:
4、写解
3、求解
2、代入
把变形后的方程代入到另一个方程中,消去一个元
分别求出两个未知数的值
写出方程组的解
1、变形
用含有一个未知数的代数式表示另一个未知数,写成y=ax+b或x=ay+b
消元: 二元
1、解二元一次方程组的基本思路是什么?
2、用代入法解方程的步骤是什么?
一元
复习:
解法一:设胜x场,负y场,则有
x+y=10①
2x+y=16②
篮球联赛中,每场都要分出胜负,每队胜一场得2分,负一场得1分,某队为了争取较好的名次,想在全部的10场比赛中得到16分,那么这个队胜负应该分别是多少?
新课导入
x+y=10
2x+y=16
这两个方程中未知数y的系数相同,
①
②
②-①可消去未知数y得
把x=6代入①,得 y=4.
①-②也能消去
未知数y,求得
x吗
像这样,通过对方程组中的两个方程进行加或减的运算就
可以消去一个未知数,得到一个一元一次方程,这种方法叫做
加减消元法,简称加减法.
x=6
(②-①等式性质)
联系上面的方法,想一想应怎样解方程组
4x+10y=3.6
15x-10y=8
①②
解:①+②, 得 19x=11.6
x=
二元一次方程组
4x+10y=3.6
15x-10y=8
一元一次方程
19x=11.6
x=
y=
把x=
代入①,得y=
∴ 这个方程组的解为
x=
y=
①+②
同减异加
归纳:
我们发现,如果二元一次方程组的两个方程中
某个未知数的系数相同或互为相反数,就可以直接用
加减法显得非常简便.
例1.用加减法解下列方程组:
(1)
4x+y=2
4x-3y=-6
①②
解: (1)①-②, 得
4y=8
y=2
把y=2代入方程①,得
x=0
3x + 7y = 27 ①
4x - 7y =-13 ②
(2)
解:
① + ②,得
7x = 14
把 x = 2 代入①,得
3 ×2 + 7y = 27
y= 3
所以原方程组的解是
x = 2
y = 3
所以原方程组的解是
x = 0
y = 2
(1) ①×2-②, 得
4x=5
x=1.25
把x=1.25代入②,得
y=-2.375
3x+2y=-1
2x+4y=-7
(1)
所以,原方程组的解为
x = 1.25
y = -2.375
① ②
例2:
(3)
7x+3y=36
2x+9y=51
系数的绝对值成倍数关系:
归纳:当两个方程中某个未知数的
系数成倍数关系时,我们也可以用加
减法,只不过在加或减之前,可先将一
个方程变形成与另一个方程中相同
未知数的系数相同,这样就可以达到
消元的目的.
① ②
看一看下面这个例子,我们又该如何解决呢
3x+4y=16
5x-6y=33
能用加减法做吗 怎么做呢 试试看!
解:① × 3 ,得:9x+12y=48 ③
②×2,得:10x-12y=66 ④
③十④,得:19x= 11
x=6
把x=6代入①得 3x6+4y=16
y=-1/2
所以原方程组的解为 x=6
y=-1/2
例3:
例4: 用加减法解方程组
4x+5y=23 ①
5x-2y=4 ②
解:①×2,得 8x+10y=46 ③
②×5,得 25x-10y=20 ④
③+④,得 33x=66 x=2
把x=2代入②,得 5×2-2y=4, y=3
所以这个方程组的解是
x=2
y=3
(1)
(2)
加减法归纳:
用加减法解同一个未知数的系数绝对值不相等,且不成整数倍的二元一次方程组时,把一个(或两个)方程的两边乘以适当的数,使两个方程中某一未知数的系数绝对值相等,从而化为第一类型方程组求解.
解:原方程组变形为
①-②,得:2y=2 y=1
把y=1代入①,得x=2
例5 用加减法解方程组
2(2x+1)=15-5y
3(y+1)=14-4x
4x+5y=13 ①
4x+3y=11 ②
x=2
y=1
所以原方程组的解是
解:由①×6,得
3x+2y=9 ③
由②×15,得
5x-3y=15 ④
例6 用加减法解方程组
②
①
③④组成一个新的方程组:
3x+2y=9 ③
5x-3y=15 ④
③×3,得 9x+6y=27 ⑤
④×2,得 10x-6y=30 ⑥
⑤+⑥,得 19x= 57 x=3
把x= 3代入③,得
3×3+2y=9
y=0
所以原方程组的解是
x=3
y=0
对于较复杂的二元一次方程组,应先化简(去分母,去括号, 合并同类项等),通常要把每个方程整理成含未知数的项在方程的左边,常数项在方程的右边的形式,再作加减消元的考虑。
注意:
复杂方程先化简
基本思路:
主要步骤:
加减消元:
二元
一元
加减消元法解方程组基本思路是什么?主要步骤有哪些?
处理系数
同一个未知数的系
数变成相同或相反的数
代入
求值2
写解
写出方程组的解
加/减
求值1
解方程组:
解:原方程组可化为:
2x+3y=4 ③
2x - y=8 ④
由③-④得: y= -1
所以原方程组
的解是
把y= -1代入② ,
解得:
②
①
方法1:
由 ④得: y= 2x-8
⑤
把⑤代入③ ,得:
2x+3 (2x-8) =4
x=7/2
把x=7/2代入⑤得
y=-1
方法2:
主要步骤:
基本思路:
写解
求解
加减
二元变一元
加减消元:
消去一个元
求出两个未知数的值
写出方程组的解
加减消元法解方程组基本思路和主要步骤:
变形
同一个未知数的系数相同或互为相反数
每个二元一次方程组均可采用代入法和加减法求解,但在解题中
要根据方程组的特点灵活选用最恰当的方法,使计算过程更简便。
当化简后的方程组存在一个方程的某个未知数系数的绝对值是1或
有一个方程的常数项是0时,用代入法;当两个方程中某个未知数
的绝对值相等或整数倍时,用加减法。
例 7: 2台大收割机和5台小收割机工作2小时收割小麦3.6公顷,3台大收割机和2台小收割机工作5小时收割小麦8公顷,1台大收割机和1台小收割机1小时各收割小麦多少公顷?
解:设1台大收割机和1台小收割机1小时各收割小麦x公顷和y公顷
化简,得:
①
②
②-①,得: 11x=4.4,
解得 x=0.4
把x=0.4代入①中,得:y=0.2
所以原方程组的解是
答:1台大收割机和1台小收割机1小时各收割小麦0.4公顷和0.2公顷。
例8: 两个完全相同的纸杯中盛有相同重量的水,现将第一个纸杯中的若干重量的水倒入第二个纸杯中,称得第一个纸杯重50克,第二个纸杯重90克(纸杯本身的重量忽略不计),问原来纸杯中各盛有多少克水?从第一个纸杯中倒了多少克水到第二个纸杯中?
解:设原来纸杯中盛有x克水,从第一个纸杯中倒入第二个纸杯中的水为y克,根据题意,得
x-y=50 ①
x+y=90 ②
①+②得:(x-y)+(x+y)=50+90,
则有 2x=50+90 所以 x=70
或者:
②-①得 :(x+y) -(x-y)=90-50,
则有 2y=40 所以 y=20
x-y=50 ①
x+y=90 ②
上述方程的另一种解法是:
例9 已知方程组
与方程组
的解相同,求a,b的值.
ax-by=4
ax+by=2
4x+3y=11
4x-5y=3
解方程组
得
解:
4x+3y=11
4x-5y=3
把x=2,y=1代入 得,
ax-by=4
ax+by=2
x=2
y=1
2a-b=4
2a+b=2
解得
a=1.5
b=-1
例10 解关于x,y的方程组
4x+3ky+1=0 ①
6y-4x=1 ②
解:①+②得(3k+6)y=0
即(2+k)y=0
(1)当k≠-2时,y=0
(2)当k=-2时,则k+2=0,(2+k)y=0恒成立
原方程组有无数组解.
把y=0代入②,得 -4x=1
y=0
例11 已知4|5x+3y-23| +5(x+4y-8)2 = 0 ,求x-y的值.
解:由题知,
5x+3y-23=0 ①
x+4y-8=0 ②
解这个方程组,得
x=4
y=1
所以 x-y=4-1=3
例12 已知4x3a+b-3 +3y2a-b=2,是关于x、y的二元一次方程,试求a、b的值.
解:根据题意:得
3a+b-3=1
2a-b=1
解,得
a=1
b=1
解:由已知得
3x-2y- 8z=0 ①
2x+y-10z=0 ②
例13 已知:3x-2y-8z=0,2x+y-10z=0,且x,y,z均不为零,求 的值.
解得
x=4z
y=2z
把x=4z,y=2z代入所求代数式,解得
例13 当x = 2与x = -3时,代数式2x2+ax-b的值都是9,求a, b 的值.
解:把x=2,x=-3代入2x2+ax-b,得
8+2a-b=9
18-3a-b=9
即
2a-b=1
3a+b=9
解,得
a=2
b=3
例14 a 为何值时,方程组 的解互为相反数,并求它的值.
2x-7y=9a
3x+4y=a-6
解:若方程组的解互为相反数,则有y=-x,将y=-x代入原方程组,得
2x+7x=9a
3x-4x=a-6
解,得
x=3
a=3
当a=3时,原方程组中的解互为相反数,
即
x=3
y=-3
例15 m , n 为何值时,5x4m-ny3m+2n与3x5y6m是同类项.
解:根据同类项的定义,有
4m-n=5
3m+2n=6m
解,得
m=2
n=3
1.代入消元法解二元一次方程组
对于用代入法解未知数系数的绝对值不是1的二元一次方程组,解题时应选择未知数的系数绝对值比较小的一个方程进行变形,这样运算简便.
课堂小结
用加减法解二元一次方程组的思想:“二元”消元转化为“一元”.条件:某一未知数系数绝对值相等.
2.用加减消元法解二元一次方程组
2.若(x-2y-3)2+(2x-y-3)2=0, 则x、y的
值是x=___,y=______.
1
-1
1.二元一次方程组 的解是________.
4x-y=5
5x+2y=10
x=0
y=-5
3.已知│x+y-5│+(2x-3y+10)2=0,则
x=____,y=____.
1
4
随堂练习
4.己知: ,则方程组
的解是___________.
x=2,y=3
5.已知(3m+2n-16)2与|3m-n-1|互为相反数,
则m+2n=_______.
12
6.若方程 (a2-9)x2+(2-4a)x+(a+4)y+
3a-5=0 是二元一次方程,则a的值为__.
±3
7.已知5a3xb2x-y和-9a8-yb7是同类项,则2xy=____.
-6
2
3
8.若方程组 与 方程组
同解,则 m=______,n=______.
9.下列方程组中,
x=_____,y=______.
4
2
10.已知方程组 ,且x+y=2,
则m2-2m+5的值是____.
11.当m≠__时,方程组 有一组解.
8
12.已知方程组 ,且y=3x,则m=___.
1
13.己知 ,则
的值是______.
2
14. 己知 ,则 的值是
_______.
2
15.如果二元一次方程组
ax-by=1,
3ax+2by=23
的解是
x=5
y=4.
求a-b的值.
1、若方程组 的解满足
2x-5y=-1,则m 为多少?
2、若(3x+2y-5)2+|5x+3y-8|=0
求x2+y-1的值。
x+y=8m
x-y=2m
