6.1分类加法计数原理与分步乘法计数原理课件 (共21张PPT)
文档属性
| 名称 | 6.1分类加法计数原理与分步乘法计数原理课件 (共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 182.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-20 19:23:39 | ||
图片预览








文档简介
(共21张PPT)
6.1分类加法计数原理与
分步乘法计数原理
思考:用一个大写的英文字母或一个阿拉伯数字(0~9)
给教室的座位编号,总共编出多少种不同的号码?
分类加法计数原理:完成一件事有两类方案,在第一类方案中有m种不同的方法,在第二类方案中有n种不同的方法那么完成这件事共有
种不同的方法。
P2 例1
P3 练习3
注:两类不同方案中的方法独立
N=m+n
分类加法计数原理
问题 1. 从甲地到乙地,可以乘火车,也可以乘汽车,还可以乘轮船。一天中,火车有4 班, 汽车有2班,轮船有3班。那么一天中乘坐这些交通工具从甲地到乙地共有多少种不同的走法
分析: 从甲地到乙地有3类方法,
第一类方法, 乘火车,有4种方法;
第二类方法, 乘汽车,有2种方法;
第三类方法, 乘轮船, 有3种方法;
所以 从甲地到乙地共有 4 + 2 + 3 = 9 种方法。
分类加法计数原理:做一件事情,完成它可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法。那么完成这件事共有
种不同的方法。
N=m1+m2+…+mn
分步乘法计数原理
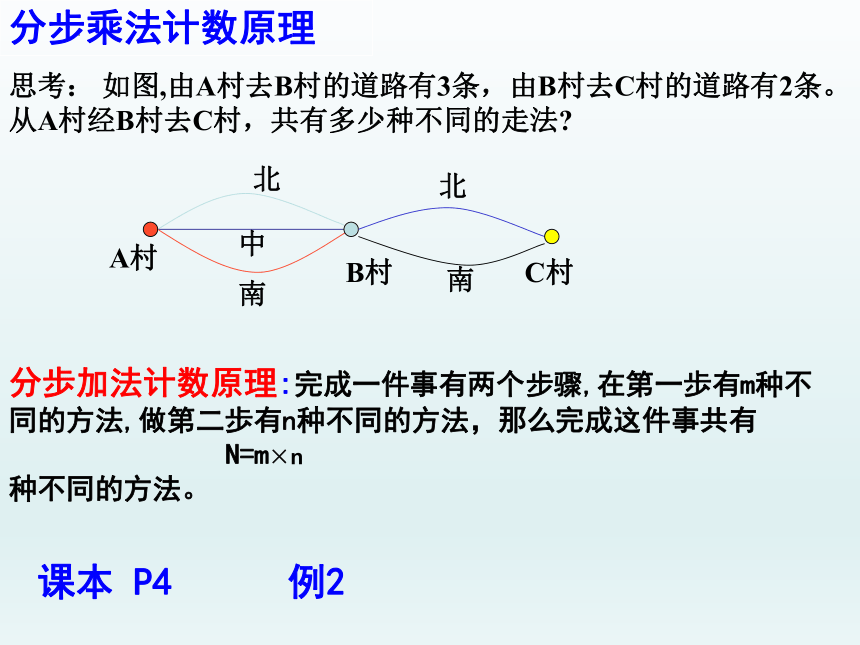
思考: 如图,由A村去B村的道路有3条,由B村去C村的道路有2条。
从A村经B村去C村,共有多少种不同的走法
A村
B村
C村
北
南
中
北
南
分歩加法计数原理:完成一件事有两个步骤,在第一歩有m种不同的方法,做第二歩有n种不同的方法,那么完成这件事共有
N=m×n
种不同的方法。
课本 P4 例2
分步乘法计数原理 : 做一件事情,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事有
种不同的方法。
分步乘法计数原理
课本 P6 练习1,2
N=m1×m2×…×mn
例1、 书架的第1层放有4本不同的计算机书,
第2层放有3本不同的文艺书,第3层放2本不同的
体育书.
①从书架上任取1本书,有多少种不同的取法?
②从书架的第1、2、3层各取1本书,有多少种不
同的取法?
例2、 要从甲、乙、丙3幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,问共有多少种不同的挂法?
例3、 一个三位密码锁,各位上数字由0,1,2,3,4,5,6,
7,8,9十个数字组成,
(1)可以设置多少种三位数的密码?
(各位上的数字允许重复)
(2)首位数字不为0的密码数是多少?
(3)首位数字是0的密码数又是多少?
例4、现高一4个班学生34人,其中一、二、三、四班分别有7人,8人,9人,10人,他们自愿组成数学课外活动小组.
(1)选其中一人为负责人,有多少种不同的选法?
(2)每班选一名组长,有多少种不同的选法?
(3)推选二人作中心发言,这二人需来自不同的班级,
有多少种不同的选法?
练习、如图,从甲地到乙地有2条路可通,从乙地到丙地有3条路可通;从甲地到丁地有4条路可通, 从丁地到丙地有2条路可通。从甲地到丙地共有多少种不同的走法?
甲地
乙地
丙地
丁地
解:从总体上看,由甲到丙有两类不同的走法,
第一类, 由甲经乙去丙,又需分两步, 所以 m1 = 2×3 = 6 种不同的走法;
第二类, 由甲经丁去丙,也需分两步, 所以 m2 = 4×2 = 8 种不同的走法;
所以从甲地到丙地共有 N = 6 + 8 = 14 种不同的走法。
分类加法与
分步乘法精练
A
U
C
C
U
U
A
A
A
G
G
例1:用0,1,2,3,4,5这六个数字,
(1)可以组成多少个数字无重复的四位数
(2)可以组成多少个数字无重复的四位偶数
排数字问题
例题补充
例2、如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?
例题补充
染色问题
①
⑤
②
③
④
变式练习2、 用红、黄、蓝3种颜色给下图中① ② ③ ④ ⑤五个区域涂色,要求相邻两个区域的颜色不同,有多少种不同的涂法?
12
变式练习1、某班宣传小组要出一期向英雄学习的专刊,现有红、黄、白、绿、蓝五种颜色的粉笔供选用,要求在黑板中A、B、C、D每一部分只写一种颜色,如图所示,相邻两块颜色不同,则不同颜色的书写方法共有________种.
180
例3、4名同学分别报名参加学校的足球队、篮球队、乒乓球队,每人限报其中的一个运动队,共有多少种报法?
练习、3各班分别从5个景点中选择一处浏览,共有多少种选法?
练习、 四名研究生各从A、B、 C三位教授中选一位作自己的导师,共有______种选法;
三名教授各从四名研究生中选一位作自己的学生,共有_____种选法。
43
34
……
…...
A
B
A
B
m1
m1
m2
m2
mn
mn
点评: 我们可以把加法原理看成“并联电路”;乘法原理看成“串联电路”。如图:
变式练习2、将红、黄、绿、黑四种不同的颜色涂入图中的5个区域内,要求相邻的颜色都不相同,则有多少种不同的涂法?
6.1分类加法计数原理与
分步乘法计数原理
思考:用一个大写的英文字母或一个阿拉伯数字(0~9)
给教室的座位编号,总共编出多少种不同的号码?
分类加法计数原理:完成一件事有两类方案,在第一类方案中有m种不同的方法,在第二类方案中有n种不同的方法那么完成这件事共有
种不同的方法。
P2 例1
P3 练习3
注:两类不同方案中的方法独立
N=m+n
分类加法计数原理
问题 1. 从甲地到乙地,可以乘火车,也可以乘汽车,还可以乘轮船。一天中,火车有4 班, 汽车有2班,轮船有3班。那么一天中乘坐这些交通工具从甲地到乙地共有多少种不同的走法
分析: 从甲地到乙地有3类方法,
第一类方法, 乘火车,有4种方法;
第二类方法, 乘汽车,有2种方法;
第三类方法, 乘轮船, 有3种方法;
所以 从甲地到乙地共有 4 + 2 + 3 = 9 种方法。
分类加法计数原理:做一件事情,完成它可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法。那么完成这件事共有
种不同的方法。
N=m1+m2+…+mn
分步乘法计数原理
思考: 如图,由A村去B村的道路有3条,由B村去C村的道路有2条。
从A村经B村去C村,共有多少种不同的走法
A村
B村
C村
北
南
中
北
南
分歩加法计数原理:完成一件事有两个步骤,在第一歩有m种不同的方法,做第二歩有n种不同的方法,那么完成这件事共有
N=m×n
种不同的方法。
课本 P4 例2
分步乘法计数原理 : 做一件事情,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事有
种不同的方法。
分步乘法计数原理
课本 P6 练习1,2
N=m1×m2×…×mn
例1、 书架的第1层放有4本不同的计算机书,
第2层放有3本不同的文艺书,第3层放2本不同的
体育书.
①从书架上任取1本书,有多少种不同的取法?
②从书架的第1、2、3层各取1本书,有多少种不
同的取法?
例2、 要从甲、乙、丙3幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,问共有多少种不同的挂法?
例3、 一个三位密码锁,各位上数字由0,1,2,3,4,5,6,
7,8,9十个数字组成,
(1)可以设置多少种三位数的密码?
(各位上的数字允许重复)
(2)首位数字不为0的密码数是多少?
(3)首位数字是0的密码数又是多少?
例4、现高一4个班学生34人,其中一、二、三、四班分别有7人,8人,9人,10人,他们自愿组成数学课外活动小组.
(1)选其中一人为负责人,有多少种不同的选法?
(2)每班选一名组长,有多少种不同的选法?
(3)推选二人作中心发言,这二人需来自不同的班级,
有多少种不同的选法?
练习、如图,从甲地到乙地有2条路可通,从乙地到丙地有3条路可通;从甲地到丁地有4条路可通, 从丁地到丙地有2条路可通。从甲地到丙地共有多少种不同的走法?
甲地
乙地
丙地
丁地
解:从总体上看,由甲到丙有两类不同的走法,
第一类, 由甲经乙去丙,又需分两步, 所以 m1 = 2×3 = 6 种不同的走法;
第二类, 由甲经丁去丙,也需分两步, 所以 m2 = 4×2 = 8 种不同的走法;
所以从甲地到丙地共有 N = 6 + 8 = 14 种不同的走法。
分类加法与
分步乘法精练
A
U
C
C
U
U
A
A
A
G
G
例1:用0,1,2,3,4,5这六个数字,
(1)可以组成多少个数字无重复的四位数
(2)可以组成多少个数字无重复的四位偶数
排数字问题
例题补充
例2、如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?
例题补充
染色问题
①
⑤
②
③
④
变式练习2、 用红、黄、蓝3种颜色给下图中① ② ③ ④ ⑤五个区域涂色,要求相邻两个区域的颜色不同,有多少种不同的涂法?
12
变式练习1、某班宣传小组要出一期向英雄学习的专刊,现有红、黄、白、绿、蓝五种颜色的粉笔供选用,要求在黑板中A、B、C、D每一部分只写一种颜色,如图所示,相邻两块颜色不同,则不同颜色的书写方法共有________种.
180
例3、4名同学分别报名参加学校的足球队、篮球队、乒乓球队,每人限报其中的一个运动队,共有多少种报法?
练习、3各班分别从5个景点中选择一处浏览,共有多少种选法?
练习、 四名研究生各从A、B、 C三位教授中选一位作自己的导师,共有______种选法;
三名教授各从四名研究生中选一位作自己的学生,共有_____种选法。
43
34
……
…...
A
B
A
B
m1
m1
m2
m2
mn
mn
点评: 我们可以把加法原理看成“并联电路”;乘法原理看成“串联电路”。如图:
变式练习2、将红、黄、绿、黑四种不同的颜色涂入图中的5个区域内,要求相邻的颜色都不相同,则有多少种不同的涂法?
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
