18.1.2 平行四边形的判定课时练习题(含答案)
文档属性
| 名称 | 18.1.2 平行四边形的判定课时练习题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 454.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-21 08:16:57 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版八年级数学下册《18.1.2平行四边形的判定》课时练习题(含答案)
一、单选题
1.下列命题中,正确的是( )
A.一组对边平行且另一组对边相等的四边形是平行四边形
B.两组邻边分别相等的四边形是平行四边形
C.两组对边分别平行的四边形是平行四边形
D.对角线互相垂直的四边形是平行四边形
2.如图,AD为△ABC中∠ BAC的外角平分线,BD⊥AD于D,E为BC中点,DE=5,AC=3,则AB长为()
A.8.5 B.8 C.7.5 D.7
3.若△ABC的三条中位线的长度分别为3cm,4cm,5cm,那么这个三角形的周长是( )
A.6cm B.12cm C.24cm D.48cm
4.如图,EF过 ABCD的对角线的交点O,且分别交AB,CD于点E,F,那么阴影部分的面积是 ABCD面积的( )
A. B. C. D.
5.如图,的周长为,对角线、相交于点,点是的中点,,则的周长为( )
A. B. C. D.
6.如图,是等边的边上一点,四边形是平行四边形,点在的延长线上,是的中点,连接.若,,则的长为( )
A.2 B.2.5 C.3 D.3.5
7.如图,在 ABCD中,延长CD到E,使DE=CD,连接BE交AD于点F,交AC于点G.下列结论正确的是( )
A.DE=DF B.AG=GF C.AF=DF D.BG=GC
8.如图,A,B两地被池塘隔开,小明先在直线AB外选一点C,然后步测出AC,BC的中点M,N,并步测出MN的长为6.5m.由此,他可以知道A.B间的距离为( )
A.12m B.12.5m C.13m D.13.5m
9.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A., B.,
C., D.,
10.下列命题正确的有( )
①如果等腰三角形的底角为15°,那么腰上的高是腰长的一半;
②三角形至少有一个内角不大于60°;
③连结任意四边形各边中点形成的新四边形是平行四边形;
④十边形内角和为1800°.
A.1个 B.2个 C.3个 D.4个
二、填空题
11.点D、E分别是△ABC边AB、AC的中点,已知BC=12,则DE=_____
12.如图,在△ABC中,AB=AC,AD是△ABC的角平分线,CE是△ABC的中线,连接 DE,若AB=6,则DE=____.
13.如图,的周长为28,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若,则PQ的长是______.
14.如图,D、E分别是AC和AB上的点,AD=DC=8,DE=6,DE∥BC,∠C=90°,将△ADE沿着AB边向右平移,当点D落在BC上时,平移的距离为______.
15.如图,平行四边形ABCD的对角线AC,BD的交点为O,AC⊥AB,CD边的中点为E.若OA=2,AB=3,则OE=__.
三、解答题
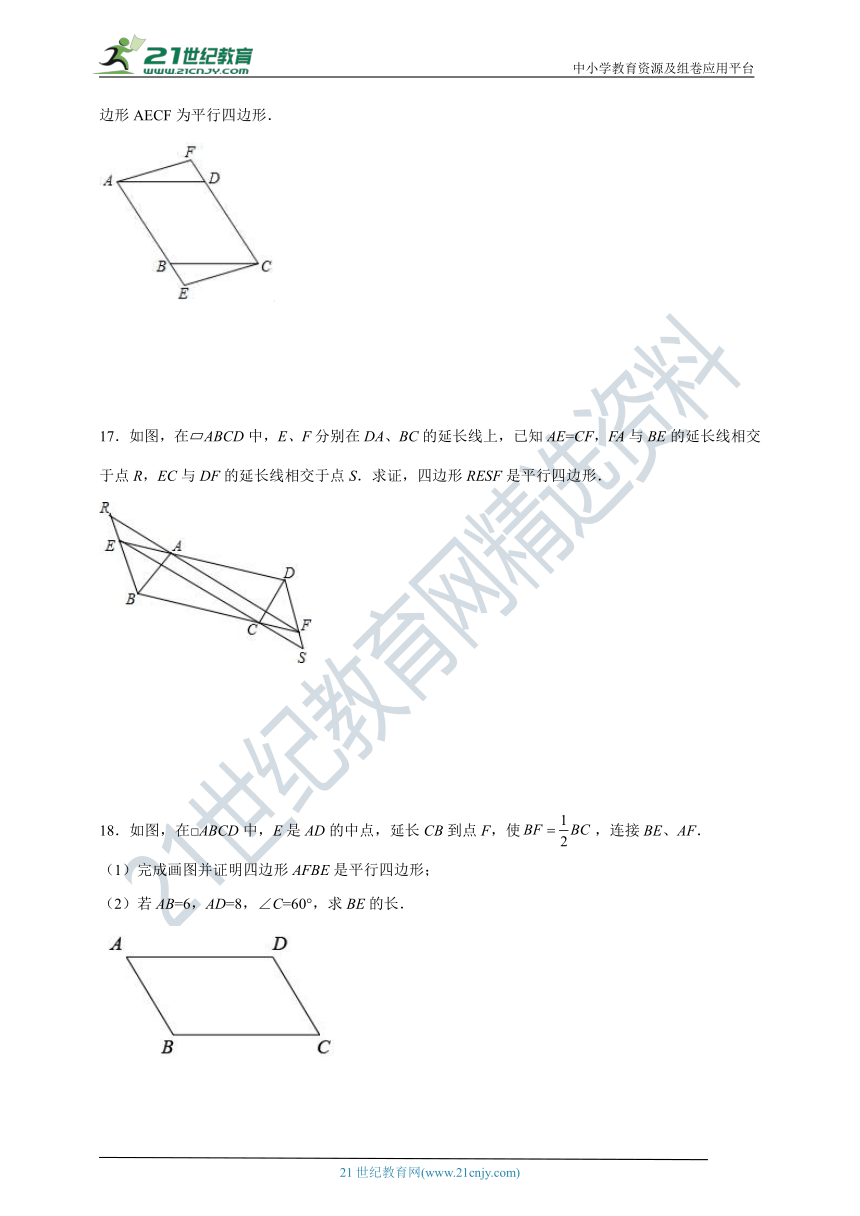
16.如图,分别延长 ABCD的边AB、CD至点E、点F,连接CE、AF,其中∠E=∠F.求证:四边形AECF为平行四边形.
17.如图,在 ABCD中,E、F分别在DA、BC的延长线上,已知AE=CF,FA与BE的延长线相交于点R,EC与DF的延长线相交于点S.求证,四边形RESF是平行四边形.
18.如图,在□ABCD中,E是AD的中点,延长CB到点F,使,连接BE、AF.
(1)完成画图并证明四边形AFBE是平行四边形;
(2)若AB=6,AD=8,∠C=60°,求BE的长.
19.如图,△ABC中,BE⊥AC于点E,AD⊥BC于点D,连接DE.
(1)若AB=BC,DE=1,BE=3,求△ABC的周长;
(2)如图2,若AB=BC,AD=BD,∠ADB的角平分线DF交BE于点F,求证:BF=DE;
(3)如图3,若AB≠BC,AD=BD,将△ADC沿着AC翻折得到△AGC,连接DG、EG,请猜想线段AE、BE、DG之间的数量关系,并证明你的结论.
参考答案
1.C2.D3.C4.C5.A6.D7.C8.C9.B10.C
11.6
12.3
13.4
14.10
15.2.5
16.∵四边形ABCD是平行四边形
∴AB=CD,AD=BC,∠ADC=∠ABC
∴∠ADF=∠CBE,且∠E=∠F,AD=BC
∴△ADF≌△CBE(AAS)
∴AF=CE,DF=BE
∴AB+BE=CD+DF
∴AE=CF,且AF=CE
∴四边形AECF是平行四边形
17.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,
∴四边形BFDE是平行四边形,
∴BR∥DS,
∵AE=CF,AE∥CF,
∴四边形AECF是平行四边形,
∴AF∥EC,
∴四边形RESF是平行四边形.
18.解:(1)∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
又E是AD的中点,,
∴AE∥BF,AE=BF,
∴四边形AFBE是平行四边形;
(2)过点A作AG⊥BF于G ,
由□ABCD可知∠ABF=∠C=60°,
又AB=6,AD=8,
∴BG=3,FG=1,AG=,
∴BE=AF=.
19.(1)如图1所示:
∵AB=BC,BE⊥AC,
∴AE=CE,∠AEB=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴DE=AC=AE,
∴AC=2DE=2,AE=1,
∴AB=,
∴BC=,
∴△ABC的周长=AB+BC+AC=2+2;
(2)连接AF,如图2所示:
∵AB=BC,BE⊥AC,
∴∠3=∠4,
∵∠ADC=90°,AD=BD,
∴△ABD是等腰直角三角形,
∴∠DAB=∠DBA=45°,
∴∠3=22.5°,
∵∠1+∠C=∠3+∠C=90°,
∴∠1=∠3=22.5°,
∵DF平分∠ABD,
∴∠ADF=∠BDF,
在△ADF和△BDF中,
,
∴△ADF≌△BDF(SAS),
∴AF=BF,∠2=∠3=22.5°,
∴∠EAF=∠1+∠2=45°,
∴△AEF是等腰直角三角形,
∴AF=AE,
∵DE=AE,
∴BF=DE;
(3)BE=DG+AE;理由如下:
作DH⊥DE交BE于H,如图3所示:
∵BE⊥AC,AD⊥BC,
∴∠1+∠ACD=∠2+∠ACD=90°,
∴∠1=∠2,
∴∠ADE=90°-∠ADH=∠BDH,
在△ADE和△BDH中,
,
∴△ADE≌△BDH(ASA),
∴DH=DE,AE=BH,
∴△DHE是等腰直角三角形,
∴∠DEH=45°,
∴∠3=90°-∠DEH=45°,
∵△ACD翻折至△ACG,
∴DE=GE,∠3=∠4=45°,
∴∠DEG=∠EDH=90°,DH=GE,
∴DH∥GE,
∴四边形DHEG是平行四边形,
∴DG=EH,
∴BE=EH+BH=DG+AE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级数学下册《18.1.2平行四边形的判定》课时练习题(含答案)
一、单选题
1.下列命题中,正确的是( )
A.一组对边平行且另一组对边相等的四边形是平行四边形
B.两组邻边分别相等的四边形是平行四边形
C.两组对边分别平行的四边形是平行四边形
D.对角线互相垂直的四边形是平行四边形
2.如图,AD为△ABC中∠ BAC的外角平分线,BD⊥AD于D,E为BC中点,DE=5,AC=3,则AB长为()
A.8.5 B.8 C.7.5 D.7
3.若△ABC的三条中位线的长度分别为3cm,4cm,5cm,那么这个三角形的周长是( )
A.6cm B.12cm C.24cm D.48cm
4.如图,EF过 ABCD的对角线的交点O,且分别交AB,CD于点E,F,那么阴影部分的面积是 ABCD面积的( )
A. B. C. D.
5.如图,的周长为,对角线、相交于点,点是的中点,,则的周长为( )
A. B. C. D.
6.如图,是等边的边上一点,四边形是平行四边形,点在的延长线上,是的中点,连接.若,,则的长为( )
A.2 B.2.5 C.3 D.3.5
7.如图,在 ABCD中,延长CD到E,使DE=CD,连接BE交AD于点F,交AC于点G.下列结论正确的是( )
A.DE=DF B.AG=GF C.AF=DF D.BG=GC
8.如图,A,B两地被池塘隔开,小明先在直线AB外选一点C,然后步测出AC,BC的中点M,N,并步测出MN的长为6.5m.由此,他可以知道A.B间的距离为( )
A.12m B.12.5m C.13m D.13.5m
9.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A., B.,
C., D.,
10.下列命题正确的有( )
①如果等腰三角形的底角为15°,那么腰上的高是腰长的一半;
②三角形至少有一个内角不大于60°;
③连结任意四边形各边中点形成的新四边形是平行四边形;
④十边形内角和为1800°.
A.1个 B.2个 C.3个 D.4个
二、填空题
11.点D、E分别是△ABC边AB、AC的中点,已知BC=12,则DE=_____
12.如图,在△ABC中,AB=AC,AD是△ABC的角平分线,CE是△ABC的中线,连接 DE,若AB=6,则DE=____.
13.如图,的周长为28,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若,则PQ的长是______.
14.如图,D、E分别是AC和AB上的点,AD=DC=8,DE=6,DE∥BC,∠C=90°,将△ADE沿着AB边向右平移,当点D落在BC上时,平移的距离为______.
15.如图,平行四边形ABCD的对角线AC,BD的交点为O,AC⊥AB,CD边的中点为E.若OA=2,AB=3,则OE=__.
三、解答题
16.如图,分别延长 ABCD的边AB、CD至点E、点F,连接CE、AF,其中∠E=∠F.求证:四边形AECF为平行四边形.
17.如图,在 ABCD中,E、F分别在DA、BC的延长线上,已知AE=CF,FA与BE的延长线相交于点R,EC与DF的延长线相交于点S.求证,四边形RESF是平行四边形.
18.如图,在□ABCD中,E是AD的中点,延长CB到点F,使,连接BE、AF.
(1)完成画图并证明四边形AFBE是平行四边形;
(2)若AB=6,AD=8,∠C=60°,求BE的长.
19.如图,△ABC中,BE⊥AC于点E,AD⊥BC于点D,连接DE.
(1)若AB=BC,DE=1,BE=3,求△ABC的周长;
(2)如图2,若AB=BC,AD=BD,∠ADB的角平分线DF交BE于点F,求证:BF=DE;
(3)如图3,若AB≠BC,AD=BD,将△ADC沿着AC翻折得到△AGC,连接DG、EG,请猜想线段AE、BE、DG之间的数量关系,并证明你的结论.
参考答案
1.C2.D3.C4.C5.A6.D7.C8.C9.B10.C
11.6
12.3
13.4
14.10
15.2.5
16.∵四边形ABCD是平行四边形
∴AB=CD,AD=BC,∠ADC=∠ABC
∴∠ADF=∠CBE,且∠E=∠F,AD=BC
∴△ADF≌△CBE(AAS)
∴AF=CE,DF=BE
∴AB+BE=CD+DF
∴AE=CF,且AF=CE
∴四边形AECF是平行四边形
17.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,
∴四边形BFDE是平行四边形,
∴BR∥DS,
∵AE=CF,AE∥CF,
∴四边形AECF是平行四边形,
∴AF∥EC,
∴四边形RESF是平行四边形.
18.解:(1)∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
又E是AD的中点,,
∴AE∥BF,AE=BF,
∴四边形AFBE是平行四边形;
(2)过点A作AG⊥BF于G ,
由□ABCD可知∠ABF=∠C=60°,
又AB=6,AD=8,
∴BG=3,FG=1,AG=,
∴BE=AF=.
19.(1)如图1所示:
∵AB=BC,BE⊥AC,
∴AE=CE,∠AEB=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴DE=AC=AE,
∴AC=2DE=2,AE=1,
∴AB=,
∴BC=,
∴△ABC的周长=AB+BC+AC=2+2;
(2)连接AF,如图2所示:
∵AB=BC,BE⊥AC,
∴∠3=∠4,
∵∠ADC=90°,AD=BD,
∴△ABD是等腰直角三角形,
∴∠DAB=∠DBA=45°,
∴∠3=22.5°,
∵∠1+∠C=∠3+∠C=90°,
∴∠1=∠3=22.5°,
∵DF平分∠ABD,
∴∠ADF=∠BDF,
在△ADF和△BDF中,
,
∴△ADF≌△BDF(SAS),
∴AF=BF,∠2=∠3=22.5°,
∴∠EAF=∠1+∠2=45°,
∴△AEF是等腰直角三角形,
∴AF=AE,
∵DE=AE,
∴BF=DE;
(3)BE=DG+AE;理由如下:
作DH⊥DE交BE于H,如图3所示:
∵BE⊥AC,AD⊥BC,
∴∠1+∠ACD=∠2+∠ACD=90°,
∴∠1=∠2,
∴∠ADE=90°-∠ADH=∠BDH,
在△ADE和△BDH中,
,
∴△ADE≌△BDH(ASA),
∴DH=DE,AE=BH,
∴△DHE是等腰直角三角形,
∴∠DEH=45°,
∴∠3=90°-∠DEH=45°,
∵△ACD翻折至△ACG,
∴DE=GE,∠3=∠4=45°,
∴∠DEG=∠EDH=90°,DH=GE,
∴DH∥GE,
∴四边形DHEG是平行四边形,
∴DG=EH,
∴BE=EH+BH=DG+AE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
