第18章 平行四边形复习(第2课时+专题讲解)课件(PPT17张)
文档属性
| 名称 | 第18章 平行四边形复习(第2课时+专题讲解)课件(PPT17张) |  | |
| 格式 | zip | ||
| 文件大小 | 764.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 19:20:38 | ||
图片预览





文档简介
(共17张PPT)
考点讲解
平行四边形 章节复习
| 第2课时|
考点一 平行四边形的性质与判定
例1 如图,E、F是平行四边形ABCD对角线BD上的两点,给出下列三个条件:①BE=DF;②∠AEB=∠DFC;③AF∥EC.请你从中选择一个适当的条件____,使四边形AECF是平行四边形,并证明你的结论.
证明:如图,连接AC交BD于O.
∴AO=CO,OB=OD.
又∵BE=DF,
∴OB-BE=OD-DF,∴OE=OF.
又∵AO=CO,
∴四边形AECF为平行四边形.
①
例2 在△ABC 中,AB = AC,点 D 在边 BC 所在的直线上,过点 D 作 DF∥AC 交直线 AB 于点 F,DE∥AB 交直线 AC 于点 E.
(1)当点 D 在边 BC 上时,如图①,求证:DE+DF=AC.
证明:∵ DF∥AC,DE∥AB,
∴ 四边形 AFDE 是平行四边形.
∴ AF = DE.
∵ DF∥AC,∴∠FDB = ∠C.
又∵ AB = AC,
∴ ∠B = ∠C,
∴ ∠FDB =∠B,∴ DF = BF.
∴ DE + DF = AF + BF = AB = AC.
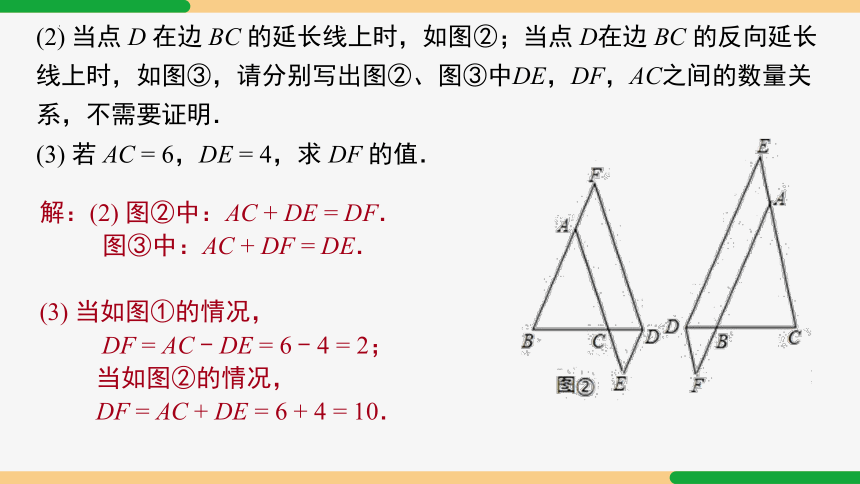
(2) 当点 D 在边 BC 的延长线上时,如图②;当点 D在边 BC 的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3) 若 AC = 6,DE = 4,求 DF 的值.
解:(2) 图②中:AC + DE = DF.
图③中:AC + DF = DE.
(3) 当如图①的情况,
DF = AC - DE = 6 - 4 = 2;
当如图②的情况,
DF = AC + DE = 6 + 4 = 10.
考点二 三角形的中位线
例3 如图,△ABC中,BD,CE为高,F是边BC的中点,判断△DEF的形状,并说明理由.
解:△DEF为等腰三角形.
在Rt△BEC中,∵F为BC的中点,
∴EF= BC.
同理:FD= BC.
∴FD=EF,
∴ △DEF为等腰三角形.
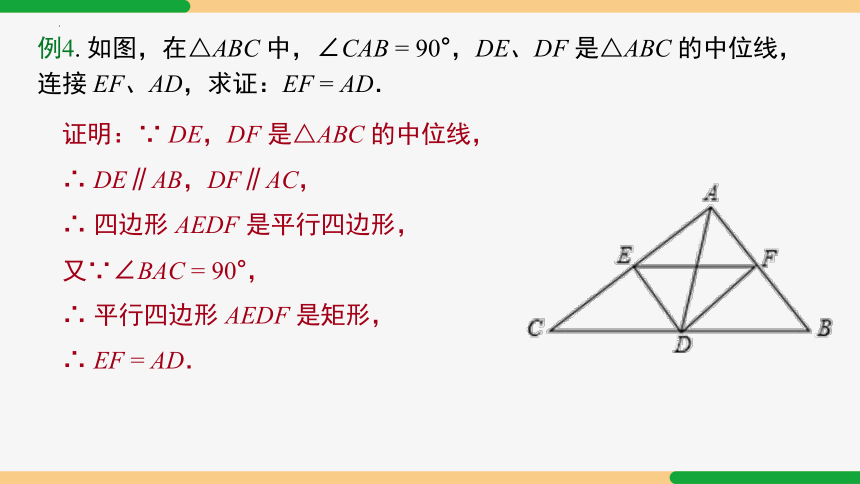
例4. 如图,在△ABC 中,∠CAB = 90°,DE、DF 是△ABC 的中位线,连接 EF、AD,求证:EF = AD.
证明:∵ DE,DF 是△ABC 的中位线,
∴ DE∥AB,DF∥AC,
∴ 四边形 AEDF 是平行四边形,
又∵∠BAC = 90°,
∴ 平行四边形 AEDF 是矩形,
∴ EF = AD.
考点三 特殊平行四边形的性质与判定
例5 如图,四边形 ABCD 是边长为 2 的正方形,点 G 是 BC 延长线上一点,连接 AG,点 E、F 分别在 AG 上,连接 BE、DF,∠1=∠2,∠3=∠4.
(1) 求证:△ABE≌△DAF;
(2) 若∠G=30°,求EF的长.
(1) 证明:∵ 四边形 ABCD 是正方形,
∴ AB = AD.
在△ABE 和△DAF 中,
∴△ABE≌△DAF (ASA).
(2) 解:∵ 四边形 ABCD 是正方形,
∴∠BAD=∠1+∠4=90°.
∵∠3=∠4,∴∠1+∠3=90°,
∴∠AFD=90°.
在正方形 ABCD 中,AD∥BC,
∴∠1=∠G=30°.
在 Rt△ADF 中,AD=2,
∴ DF=1,AF= .
由 (1) 得△ABE≌△DAF,
∴ AE=DF=1.
∴ EF=AF-AE= -1.
例6 如图,△ABC 中,点 O 是 AC 上的一动点,过点 O 作直线 MN∥BC,设 MN 交∠BCA 的平分线于点 E,交∠BCA 的外角∠ACG 的平分线于点 F,连接 AE、AF.
(1) 求证:∠ECF=90°;
(2) 当点 O 运动到何处时,四边形 AECF 是矩形?请说明理由;
(1) 证明:∵ CE 平分∠BCO,CF 平分∠GCO,
∴∠OCE=∠BCE,∠OCF=∠GCF,
∴∠ECF= ×180°=90°.
(2)解:当点 O 运动到 AC 的中点时,四边形 AECF 是矩形. 理由如下:
∵ MN∥BC,∴∠OEC=∠BCE,∠OFC=∠GCF.
又∵ CE 平分∠BCO,CF 平分∠GCO,
∴∠OCE=∠BCE,∠OCF=∠GCF.
∴∠OCE=∠OEC,∠OCF=∠OFC.
∴ OE=OC,OF=OC.
∴ OE=OF.
当点 O 运动到 AC 的中点时,OA=OC,
∴ 四边形 AECF 是平行四边形.
∵∠ECF=90°,∴ 四边形 AECF 是矩形.
解:当点 O 运动到 AC 的中点,且满足∠ACB 为直角时,四边形 AECF 是正方形.
由 (2) 知四边形 AECF 是矩形,
而 MN∥BC,当∠ACB=90° 时,
∠AOF=∠COE=∠COF=∠AOE=90°,
即AC⊥EF,
∴ 四边形AECF是正方形.
(3) 在 (2) 的条件下,△ABC 满足什么条件时, 四边形 AECF 为正方形?
例7 8.如图,四边形ABCD、DEFG都是正方形,连接AE、CG.
(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.
(1)证明:∵∠ADC=∠GDE=90°,
∴∠ADC+∠ADG=∠GDE+∠ADG,
即∠GDC=∠ADE.
又∵CD=AD,
DG=DE,
∴△GCD≌△EAD,
∴AE=CG.
(2) 观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.
(2)解:AE⊥CG.
∵由(1)知△GCD≌△EAD,
∴∠GCD=∠EAD.
又∵∠ANM=∠CND,
∴∠AMN=∠CDN=90°,
∴AE⊥CG.
考点四 本章解题思想方法——方程思想
例8 如图,折叠长方形一边 AD,点 D 落在BC 边的点 F 处,BC = 10 cm,AB = 8 cm,
求:(1) FC 的长; (2) EF 的长.
解:(1)由题意得 AF = AD = 10 cm,
在 Rt△ABF 中,∵ AB = 8,
∴ BF = 6 cm,
∴ FC = BC - BF = 10 - 6 = 4 (cm).
(2) 由题意可得 EF = DE,可设 DE 的长为 x,
在Rt△EFC中,(8 - x)2 + 42 = x2,
解得 x = 5.
即 EF 的长为 5 cm.
考点四 本章解题思想方法——分类讨论思想
例9 在一个平行四边形中,若一个角的平分线把一条边分成长是2 cm和3 cm的两条线段,求该平行四边形的周长是__________.
解:如图,∵在平行四边形ABCD中,AB = CD, AD = BC ,AD∥BC,
∴∠AEB = ∠CBE.
又∠ABE =∠CBE,
∴ ∠ABE =∠AEB,∴ AB = AE.
(1) 当 AE = 2 时,则平行四边形的周长= 2×(2+5) = 14.
(2) 当 AE = 3 时,则平行四边形的周长= 2×(3+5) = 16.
14 或16
考点四 本章解题思想方法——面积法
例10 .如图,在矩形ABCD中,AB=3,AD=4,点P在AD上,PE⊥AC于E,PF⊥BD于F,则PE+PF=____.
例11 如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于H,求高DH的长.
解:∵四边形ABCD为菱形,
∴AO= AC=4cm,AC⊥BD,
∴在Rt△AOB中,
(cm).
S△ABD= DH · AB= AO · BD
∴DH= (cm).
考点讲解
平行四边形 章节复习
| 第2课时|
考点一 平行四边形的性质与判定
例1 如图,E、F是平行四边形ABCD对角线BD上的两点,给出下列三个条件:①BE=DF;②∠AEB=∠DFC;③AF∥EC.请你从中选择一个适当的条件____,使四边形AECF是平行四边形,并证明你的结论.
证明:如图,连接AC交BD于O.
∴AO=CO,OB=OD.
又∵BE=DF,
∴OB-BE=OD-DF,∴OE=OF.
又∵AO=CO,
∴四边形AECF为平行四边形.
①
例2 在△ABC 中,AB = AC,点 D 在边 BC 所在的直线上,过点 D 作 DF∥AC 交直线 AB 于点 F,DE∥AB 交直线 AC 于点 E.
(1)当点 D 在边 BC 上时,如图①,求证:DE+DF=AC.
证明:∵ DF∥AC,DE∥AB,
∴ 四边形 AFDE 是平行四边形.
∴ AF = DE.
∵ DF∥AC,∴∠FDB = ∠C.
又∵ AB = AC,
∴ ∠B = ∠C,
∴ ∠FDB =∠B,∴ DF = BF.
∴ DE + DF = AF + BF = AB = AC.
(2) 当点 D 在边 BC 的延长线上时,如图②;当点 D在边 BC 的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3) 若 AC = 6,DE = 4,求 DF 的值.
解:(2) 图②中:AC + DE = DF.
图③中:AC + DF = DE.
(3) 当如图①的情况,
DF = AC - DE = 6 - 4 = 2;
当如图②的情况,
DF = AC + DE = 6 + 4 = 10.
考点二 三角形的中位线
例3 如图,△ABC中,BD,CE为高,F是边BC的中点,判断△DEF的形状,并说明理由.
解:△DEF为等腰三角形.
在Rt△BEC中,∵F为BC的中点,
∴EF= BC.
同理:FD= BC.
∴FD=EF,
∴ △DEF为等腰三角形.
例4. 如图,在△ABC 中,∠CAB = 90°,DE、DF 是△ABC 的中位线,连接 EF、AD,求证:EF = AD.
证明:∵ DE,DF 是△ABC 的中位线,
∴ DE∥AB,DF∥AC,
∴ 四边形 AEDF 是平行四边形,
又∵∠BAC = 90°,
∴ 平行四边形 AEDF 是矩形,
∴ EF = AD.
考点三 特殊平行四边形的性质与判定
例5 如图,四边形 ABCD 是边长为 2 的正方形,点 G 是 BC 延长线上一点,连接 AG,点 E、F 分别在 AG 上,连接 BE、DF,∠1=∠2,∠3=∠4.
(1) 求证:△ABE≌△DAF;
(2) 若∠G=30°,求EF的长.
(1) 证明:∵ 四边形 ABCD 是正方形,
∴ AB = AD.
在△ABE 和△DAF 中,
∴△ABE≌△DAF (ASA).
(2) 解:∵ 四边形 ABCD 是正方形,
∴∠BAD=∠1+∠4=90°.
∵∠3=∠4,∴∠1+∠3=90°,
∴∠AFD=90°.
在正方形 ABCD 中,AD∥BC,
∴∠1=∠G=30°.
在 Rt△ADF 中,AD=2,
∴ DF=1,AF= .
由 (1) 得△ABE≌△DAF,
∴ AE=DF=1.
∴ EF=AF-AE= -1.
例6 如图,△ABC 中,点 O 是 AC 上的一动点,过点 O 作直线 MN∥BC,设 MN 交∠BCA 的平分线于点 E,交∠BCA 的外角∠ACG 的平分线于点 F,连接 AE、AF.
(1) 求证:∠ECF=90°;
(2) 当点 O 运动到何处时,四边形 AECF 是矩形?请说明理由;
(1) 证明:∵ CE 平分∠BCO,CF 平分∠GCO,
∴∠OCE=∠BCE,∠OCF=∠GCF,
∴∠ECF= ×180°=90°.
(2)解:当点 O 运动到 AC 的中点时,四边形 AECF 是矩形. 理由如下:
∵ MN∥BC,∴∠OEC=∠BCE,∠OFC=∠GCF.
又∵ CE 平分∠BCO,CF 平分∠GCO,
∴∠OCE=∠BCE,∠OCF=∠GCF.
∴∠OCE=∠OEC,∠OCF=∠OFC.
∴ OE=OC,OF=OC.
∴ OE=OF.
当点 O 运动到 AC 的中点时,OA=OC,
∴ 四边形 AECF 是平行四边形.
∵∠ECF=90°,∴ 四边形 AECF 是矩形.
解:当点 O 运动到 AC 的中点,且满足∠ACB 为直角时,四边形 AECF 是正方形.
由 (2) 知四边形 AECF 是矩形,
而 MN∥BC,当∠ACB=90° 时,
∠AOF=∠COE=∠COF=∠AOE=90°,
即AC⊥EF,
∴ 四边形AECF是正方形.
(3) 在 (2) 的条件下,△ABC 满足什么条件时, 四边形 AECF 为正方形?
例7 8.如图,四边形ABCD、DEFG都是正方形,连接AE、CG.
(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.
(1)证明:∵∠ADC=∠GDE=90°,
∴∠ADC+∠ADG=∠GDE+∠ADG,
即∠GDC=∠ADE.
又∵CD=AD,
DG=DE,
∴△GCD≌△EAD,
∴AE=CG.
(2) 观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.
(2)解:AE⊥CG.
∵由(1)知△GCD≌△EAD,
∴∠GCD=∠EAD.
又∵∠ANM=∠CND,
∴∠AMN=∠CDN=90°,
∴AE⊥CG.
考点四 本章解题思想方法——方程思想
例8 如图,折叠长方形一边 AD,点 D 落在BC 边的点 F 处,BC = 10 cm,AB = 8 cm,
求:(1) FC 的长; (2) EF 的长.
解:(1)由题意得 AF = AD = 10 cm,
在 Rt△ABF 中,∵ AB = 8,
∴ BF = 6 cm,
∴ FC = BC - BF = 10 - 6 = 4 (cm).
(2) 由题意可得 EF = DE,可设 DE 的长为 x,
在Rt△EFC中,(8 - x)2 + 42 = x2,
解得 x = 5.
即 EF 的长为 5 cm.
考点四 本章解题思想方法——分类讨论思想
例9 在一个平行四边形中,若一个角的平分线把一条边分成长是2 cm和3 cm的两条线段,求该平行四边形的周长是__________.
解:如图,∵在平行四边形ABCD中,AB = CD, AD = BC ,AD∥BC,
∴∠AEB = ∠CBE.
又∠ABE =∠CBE,
∴ ∠ABE =∠AEB,∴ AB = AE.
(1) 当 AE = 2 时,则平行四边形的周长= 2×(2+5) = 14.
(2) 当 AE = 3 时,则平行四边形的周长= 2×(3+5) = 16.
14 或16
考点四 本章解题思想方法——面积法
例10 .如图,在矩形ABCD中,AB=3,AD=4,点P在AD上,PE⊥AC于E,PF⊥BD于F,则PE+PF=____.
例11 如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于H,求高DH的长.
解:∵四边形ABCD为菱形,
∴AO= AC=4cm,AC⊥BD,
∴在Rt△AOB中,
(cm).
S△ABD= DH · AB= AO · BD
∴DH= (cm).
