18.2.1 矩形(1)课件(PPT24张)
文档属性
| 名称 | 18.2.1 矩形(1)课件(PPT24张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 19:23:59 | ||
图片预览





文档简介
(共24张PPT)
人教版 八下
第十八章 平行四边形
18.2 特殊的平行四边形
18.2.1 矩形(1)
主讲人:
学习目标
1.理解矩形的概念,知道矩形与平行四边形的区别与联系.(重点)
2.会证明矩形的性质,会用矩形的性质解决简单的问题.(重点、难点)
3.掌握直角三角形斜边中线的性质,并会简单的运用. (重点)
D
A
B
C
课前导入
我们已经研究了平行四边形,观察下面两个图形,看看它们有什么关系?
矩形
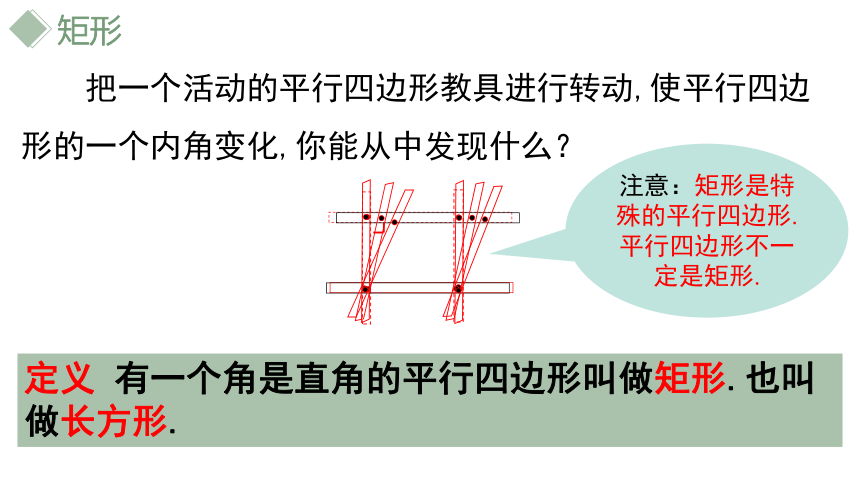
定义 有一个角是直角的平行四边形叫做矩形.也叫做长方形.
把一个活动的平行四边形教具进行转动,使平行四边形的一个内角变化,你能从中发现什么?
注意:矩形是特殊的平行四边形.
平行四边形不一定是矩形.
矩形
矩形是常见的图形,门窗框、书桌面、教科书封面、地砖等都有矩形的形象。你还能举出一些例子吗?
矩形的性质
思考 因为矩形是平行四边形,所以它具有平行四边形的所有性质,由于它有一个角为直角,它是否具有一般平行四边形不具有的一些特殊性质呢?
猜想:矩形的四个角都是直角.
矩形的对角线相等.
矩形的性质
性质1 矩形的四个角都是直角.
猜想1:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°.
证明: ∵四边形ABCD是矩形,
又∵矩形ABCD是平行四边形,
∴ ∠A=∠C , ∠B = ∠D,
∠A +∠B = 180°.
∴ ∠A=∠B=∠C=∠D=90°.
即矩形的四个角都是直角.
矩形的性质
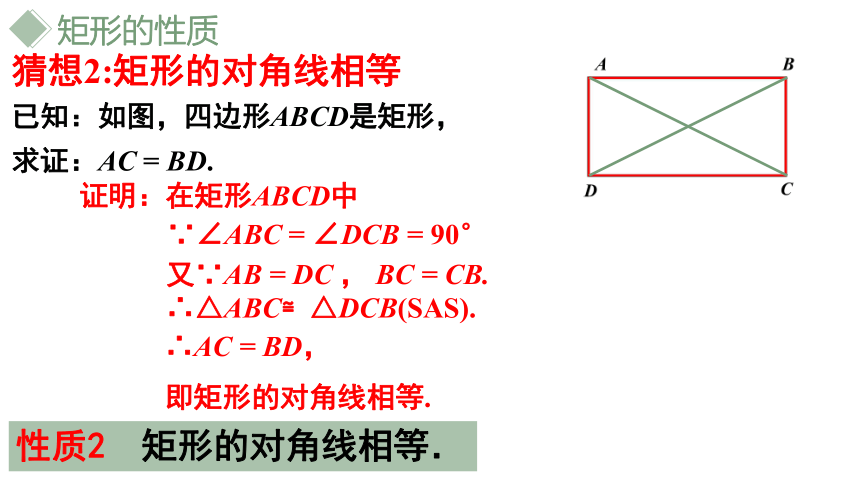
性质2 矩形的对角线相等.
已知:如图,四边形ABCD是矩形,
求证:AC = BD.
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB.
∴△ABC≌△DCB(SAS).
∴AC = BD,
即矩形的对角线相等.
猜想2:矩形的对角线相等
思考 Rt△ABC中,BO是一条怎样的线段?它的长度与斜边AC有什么关系?
直角三角形斜边上的中线的性质
O
猜想:BO=AC
直角三角形斜边上的中线的性质
直角三角形斜边上的中线等于斜边的一半.
证明: 延长BO至点D, 使OD=BO,连结AD、DC.
∵AO=OC, BO=OD,
∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∴平行四边形ABCD是矩形,
∴AC=BD,
如图,在Rt△ABC中,∠ABC=90°,BO是AC上的中线.
求证: BO =AC .
∴BO= BD= AC.
O
直角三角形斜边上的中线的性质
例1 如图,矩形ABCD的两条对角线AC,BD相交于点O,∠AOB=60°,AB=4 .求矩形对角线的长.
A
B
C
D
O
∴AC与BD相等且互相平分,
∴OA=OB=OC=OD,
∵∠AOB=60°,
∴ 矩形的对角线长 AC=BD=2OA=8.
解:∵四边形ABCD是矩形,
∴OB=OA=AB=4cm
矩形的性质
练一练 1.矩形具有而一般平行四边形不具有的性质
是 ( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分
A
矩形的性质
练一练 1.矩形具有而一般平行四边形不具有的性质
是 ( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分
A
03
巩固练习
巩固练习
1.一个矩形的一条对角线长为8,两条对角线的一个夹角为120,求矩形的边长.
∴AC与BD相等且互相平分,
∴OA=OC=AC=4,
∵∠AOD=120°, ∴ ∠COD=60°
∴ AD=
解:由题知∠AOD=120°,AC=8
∵四边形ABCD是矩形,
∴CD=OC=4
A
B
C
D
O
巩固练习
2.矩形是轴对称图形吗?如果是,它有几条对称轴?
解:矩形是轴对称图形;
有两条对称轴.
巩固练习
3.如图,在矩形ABCD中,AC与BD交于O点,BE⊥AC于E,CF⊥BD于F,求证:BE=CF.
证明:∵AC、BD为矩形ABCD的对角线,
∴OB=OC.
又∵∠BEO=∠CFO=90°,∠EOB=∠FOC.
∴Rt△EBO≌Rt△FCO,
∴BE=CF.
巩固练习
4.如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.求证:BD=BE;
证明:∵四边形ABCD是矩形,
∴AC= BD, AB∥CD.
又∵BE∥AC,
∴四边形ABEC是平行四边形,
∴AC=BE,
∴BD=BE.
巩固练习
5.如图,在矩形ABCD中,AE⊥BD于点E,∠DAE:
∠BAE=3:1,求∠BAE和∠EAO的度数.
解:∵四边形ABCD是矩形,
∴∠DAB=90°,
AO= AC,BO= BD,AC=BD,
∴∠BAE+∠DAE=90°,AO=BO.
又∵∠DAE:∠BAE=3:1,
∴∠BAE=22.5°,∠DAE=67.5°.
巩固练习
∵AE⊥BD,
∴∠ABE=90°-∠BAE=90°-22.5°=67.5°,
∴∠OAB=∠ABE=67.5°
∴∠EAO=67.5°-22.5°=45°.
04
课堂小结
课堂小结
矩形
定义:
性质
有一个角是直角的平行四边形叫做矩形.也叫做长方形.
矩形的四个角都是直角.
矩形的对角线相等.
直角三角形斜边上的中线等于斜边的一半.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 八下
第十八章 平行四边形
18.2 特殊的平行四边形
18.2.1 矩形(1)
主讲人:
学习目标
1.理解矩形的概念,知道矩形与平行四边形的区别与联系.(重点)
2.会证明矩形的性质,会用矩形的性质解决简单的问题.(重点、难点)
3.掌握直角三角形斜边中线的性质,并会简单的运用. (重点)
D
A
B
C
课前导入
我们已经研究了平行四边形,观察下面两个图形,看看它们有什么关系?
矩形
定义 有一个角是直角的平行四边形叫做矩形.也叫做长方形.
把一个活动的平行四边形教具进行转动,使平行四边形的一个内角变化,你能从中发现什么?
注意:矩形是特殊的平行四边形.
平行四边形不一定是矩形.
矩形
矩形是常见的图形,门窗框、书桌面、教科书封面、地砖等都有矩形的形象。你还能举出一些例子吗?
矩形的性质
思考 因为矩形是平行四边形,所以它具有平行四边形的所有性质,由于它有一个角为直角,它是否具有一般平行四边形不具有的一些特殊性质呢?
猜想:矩形的四个角都是直角.
矩形的对角线相等.
矩形的性质
性质1 矩形的四个角都是直角.
猜想1:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°.
证明: ∵四边形ABCD是矩形,
又∵矩形ABCD是平行四边形,
∴ ∠A=∠C , ∠B = ∠D,
∠A +∠B = 180°.
∴ ∠A=∠B=∠C=∠D=90°.
即矩形的四个角都是直角.
矩形的性质
性质2 矩形的对角线相等.
已知:如图,四边形ABCD是矩形,
求证:AC = BD.
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB.
∴△ABC≌△DCB(SAS).
∴AC = BD,
即矩形的对角线相等.
猜想2:矩形的对角线相等
思考 Rt△ABC中,BO是一条怎样的线段?它的长度与斜边AC有什么关系?
直角三角形斜边上的中线的性质
O
猜想:BO=AC
直角三角形斜边上的中线的性质
直角三角形斜边上的中线等于斜边的一半.
证明: 延长BO至点D, 使OD=BO,连结AD、DC.
∵AO=OC, BO=OD,
∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∴平行四边形ABCD是矩形,
∴AC=BD,
如图,在Rt△ABC中,∠ABC=90°,BO是AC上的中线.
求证: BO =AC .
∴BO= BD= AC.
O
直角三角形斜边上的中线的性质
例1 如图,矩形ABCD的两条对角线AC,BD相交于点O,∠AOB=60°,AB=4 .求矩形对角线的长.
A
B
C
D
O
∴AC与BD相等且互相平分,
∴OA=OB=OC=OD,
∵∠AOB=60°,
∴ 矩形的对角线长 AC=BD=2OA=8.
解:∵四边形ABCD是矩形,
∴OB=OA=AB=4cm
矩形的性质
练一练 1.矩形具有而一般平行四边形不具有的性质
是 ( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分
A
矩形的性质
练一练 1.矩形具有而一般平行四边形不具有的性质
是 ( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分
A
03
巩固练习
巩固练习
1.一个矩形的一条对角线长为8,两条对角线的一个夹角为120,求矩形的边长.
∴AC与BD相等且互相平分,
∴OA=OC=AC=4,
∵∠AOD=120°, ∴ ∠COD=60°
∴ AD=
解:由题知∠AOD=120°,AC=8
∵四边形ABCD是矩形,
∴CD=OC=4
A
B
C
D
O
巩固练习
2.矩形是轴对称图形吗?如果是,它有几条对称轴?
解:矩形是轴对称图形;
有两条对称轴.
巩固练习
3.如图,在矩形ABCD中,AC与BD交于O点,BE⊥AC于E,CF⊥BD于F,求证:BE=CF.
证明:∵AC、BD为矩形ABCD的对角线,
∴OB=OC.
又∵∠BEO=∠CFO=90°,∠EOB=∠FOC.
∴Rt△EBO≌Rt△FCO,
∴BE=CF.
巩固练习
4.如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.求证:BD=BE;
证明:∵四边形ABCD是矩形,
∴AC= BD, AB∥CD.
又∵BE∥AC,
∴四边形ABEC是平行四边形,
∴AC=BE,
∴BD=BE.
巩固练习
5.如图,在矩形ABCD中,AE⊥BD于点E,∠DAE:
∠BAE=3:1,求∠BAE和∠EAO的度数.
解:∵四边形ABCD是矩形,
∴∠DAB=90°,
AO= AC,BO= BD,AC=BD,
∴∠BAE+∠DAE=90°,AO=BO.
又∵∠DAE:∠BAE=3:1,
∴∠BAE=22.5°,∠DAE=67.5°.
巩固练习
∵AE⊥BD,
∴∠ABE=90°-∠BAE=90°-22.5°=67.5°,
∴∠OAB=∠ABE=67.5°
∴∠EAO=67.5°-22.5°=45°.
04
课堂小结
课堂小结
矩形
定义:
性质
有一个角是直角的平行四边形叫做矩形.也叫做长方形.
矩形的四个角都是直角.
矩形的对角线相等.
直角三角形斜边上的中线等于斜边的一半.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
