18.2.1 矩形(2)课件(PPT25张)
文档属性
| 名称 | 18.2.1 矩形(2)课件(PPT25张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 19:25:09 | ||
图片预览






文档简介
(共25张PPT)
人教版 八下
第十八章 平行四边形
18.2 特殊的平行四边形
18.2.1 矩形(2)
主讲人:
学习目标
1.经历矩形判定定理的猜想与证明过程,理解并掌握矩形的判定定理.(重点)
2.能应用矩形的判定解决简单的证明题和计算题.(难点)
课前导入
矩形有哪些性质呢?
具有平行四边形的一切性质;
四个角都是直角;
对角线相等。
那如何判定一个四边形或者平行四边形是矩形呢?
矩形的判定
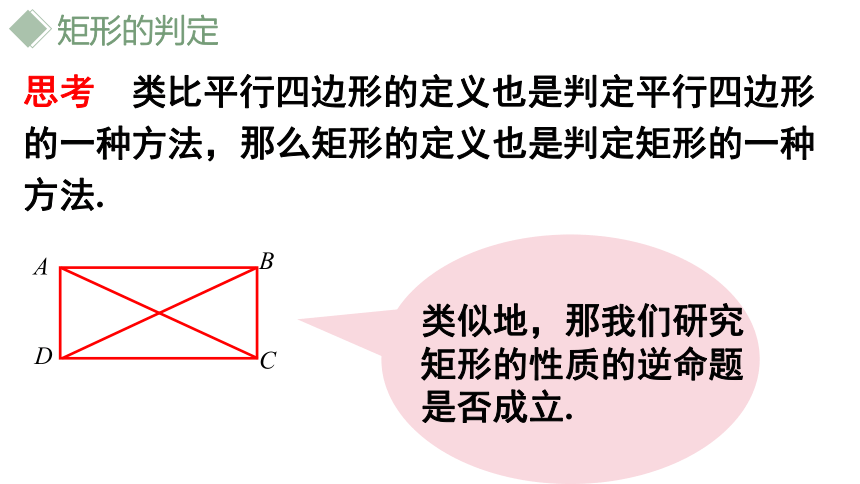
类似地,那我们研究矩形的性质的逆命题是否成立.
思考 类比平行四边形的定义也是判定平行四边形的一种方法,那么矩形的定义也是判定矩形的一种方法.
A
B
C
D
矩形的判定
思考 上节课我们已经知道“矩形的对角线相等”,反过来,对角线相等的四边形是矩形吗?
不是,平行四边形和等腰梯形的对角线也相等;
猜想:对角线相等的平行四边形是矩形.
如何证明呢?
矩形的判定
如图,在平行四边形ABCD中,对角线AC=BD.
求证:平行四边形ABCD为矩形。
证明:过点C作CE平行于BD交AB的延长线于E,
∵BD∥CE,BE∥CD
∴四边形BECD为平行四边形
∴CD=BE. 又∵AB=CD
∴AB=BE 即:B为AE的中点
又∵AC=BD BD=CE
∴AC=CE ∴CB⊥AE
综上所述:四边形ABCD为矩形.
E
矩形的判定
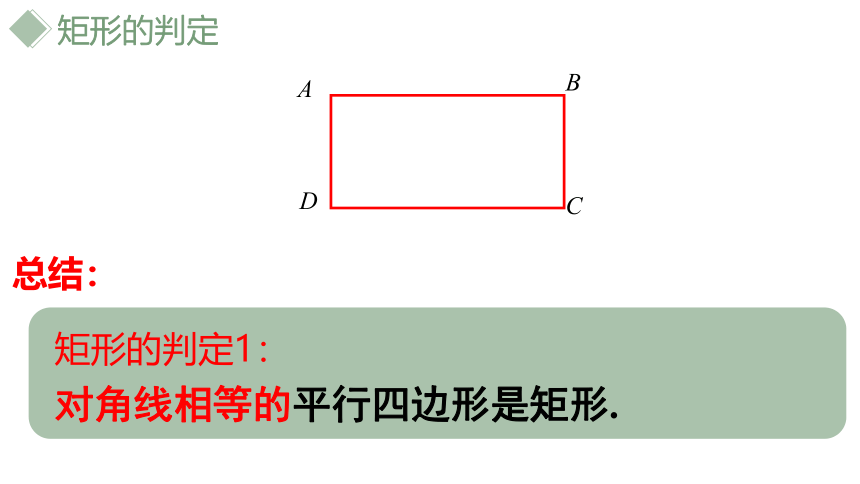
总结:
矩形的判定1:
对角线相等的平行四边形是矩形.
A
B
C
D
矩形的判定
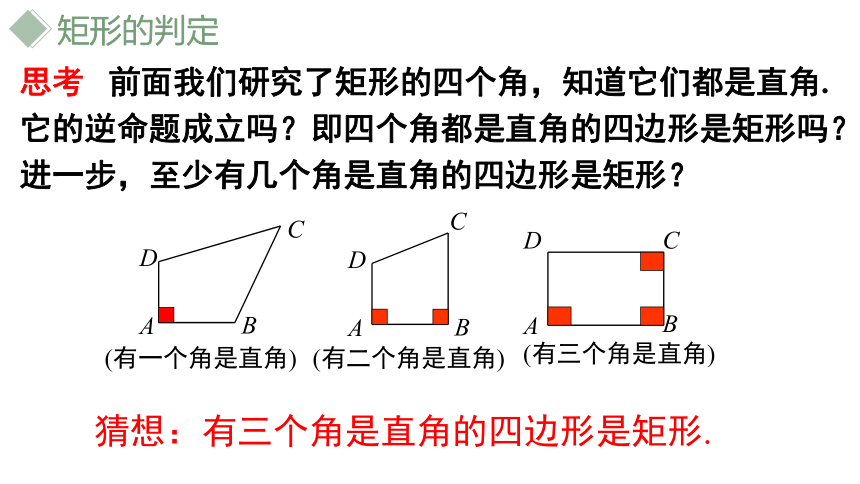
思考 前面我们研究了矩形的四个角,知道它们都是直角.它的逆命题成立吗?即四个角都是直角的四边形是矩形吗?进一步,至少有几个角是直角的四边形是矩形?
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
猜想:有三个角是直角的四边形是矩形.
矩形的判定
已知:如图, 在四边形ABCD中, ∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
A
B
C
D
矩形的判定
总结:
矩形的判定2:
有三个角是直角的四边形是矩形.
A
B
C
D
矩形的判定
例1 如图,在 ABCD中,对角线AC、BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
解:∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD= BD
又OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,∴∠BAD=90°
又∠OAD=50°,∴∠OAB=40°
平行四边形的判定
练一练 1.下列判定矩形的说法是否正确?为什么?
(1)有一个角是直角的四边形是矩形.( )
(2)四个角都相等的四边形是矩形.( )
(3)对角线相等的四边形是矩形.( )
×
√
×
03
巩固练习
巩固练习
1.八年级(3)班同学要在广场上布置一个矩形的花坛,计划用红花摆成两条对角线.如果一条对角线用了38盆红花,还需要从花房运来多少盆红花?为什么?如果一条对角线用了49盆呢?
巩固练习
解:还需要从花房运来38盆“红花”.
因为,矩形的对角线相等,所以另一条对角线也需38盆“红花”.且不应除去两条对角线的交点,这是因为38盆是偶数,因此对较线的交点没有摆花盆.
如果一条对角线用了49盆,那么应从花房运来48盆“红花”.因为矩形的对角线相等,但由于49盆是奇数,因此对角线交点应已摆放花盆,所以,另一条对角线上的花盆数应少1盆.
巩固练习
2.如图,平行四边形 ABCD的对角线AC、BD相交于点O,△OAB是等边三角形,且AB=4. 求 平行四边形ABCD的面积.
解:∵△OAB是等边三角形且平行四边形 ABCD的对角线AC、BD互相平分
∴AO=OB=OC=OD=AB=DC=4
∵∠AOB= 60°
∴∠AOD=120°
巩固练习
又∵AO=DO ,
∴∠ADC=90°.
∴四边形ABCD是矩形,
AC=8 ,DC=4, AD=4,
∴矩形ABCD的面积为1.
巩固练习
3.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E,求证:四边形ADCE为矩形.
证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,即∠DAC= ∠BAC.
又∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE= ∠CAM,
巩固练习
∴∠DAE=∠DAC+∠CAE= (∠BAC+∠CAM)=90°.
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形.
巩固练习
4.如图,在四边形ABCD中,AB∥CD,∠BAD=90°,
AB=5,BC=12,AC=13.求证:四边形ABCD是矩形.
证明:四边形ABCD中,AB∥CD,∠BAD=90°,
∴∠ADC=90°.
∵△ABC中,AB=5,BC=12,AC=13,
满足132=52+122,即
∴△ABC是直角三角形,且∠B=90°,
∴四边形ABCD是矩形.
巩固练习
5.如图,在△ABC中,D在AB边上,AD=BD=CD,DE∥AC,DF∥BC.求证:四边形DECF是矩形.
证明:∵AD=BD=CD,
∴△ABC为直角三角形,∠FCE=90°
∵DE∥AC,DF∥BC,
∴四边形DECF为平行四边形,
又∵∠FCE=90°,
∴平行四边形DECF是矩形.
04
课堂小结
课堂小结
矩形的判定定理:
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
矩形的定义:
有一个角是直角的平行四边形是矩形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 八下
第十八章 平行四边形
18.2 特殊的平行四边形
18.2.1 矩形(2)
主讲人:
学习目标
1.经历矩形判定定理的猜想与证明过程,理解并掌握矩形的判定定理.(重点)
2.能应用矩形的判定解决简单的证明题和计算题.(难点)
课前导入
矩形有哪些性质呢?
具有平行四边形的一切性质;
四个角都是直角;
对角线相等。
那如何判定一个四边形或者平行四边形是矩形呢?
矩形的判定
类似地,那我们研究矩形的性质的逆命题是否成立.
思考 类比平行四边形的定义也是判定平行四边形的一种方法,那么矩形的定义也是判定矩形的一种方法.
A
B
C
D
矩形的判定
思考 上节课我们已经知道“矩形的对角线相等”,反过来,对角线相等的四边形是矩形吗?
不是,平行四边形和等腰梯形的对角线也相等;
猜想:对角线相等的平行四边形是矩形.
如何证明呢?
矩形的判定
如图,在平行四边形ABCD中,对角线AC=BD.
求证:平行四边形ABCD为矩形。
证明:过点C作CE平行于BD交AB的延长线于E,
∵BD∥CE,BE∥CD
∴四边形BECD为平行四边形
∴CD=BE. 又∵AB=CD
∴AB=BE 即:B为AE的中点
又∵AC=BD BD=CE
∴AC=CE ∴CB⊥AE
综上所述:四边形ABCD为矩形.
E
矩形的判定
总结:
矩形的判定1:
对角线相等的平行四边形是矩形.
A
B
C
D
矩形的判定
思考 前面我们研究了矩形的四个角,知道它们都是直角.它的逆命题成立吗?即四个角都是直角的四边形是矩形吗?进一步,至少有几个角是直角的四边形是矩形?
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
猜想:有三个角是直角的四边形是矩形.
矩形的判定
已知:如图, 在四边形ABCD中, ∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
A
B
C
D
矩形的判定
总结:
矩形的判定2:
有三个角是直角的四边形是矩形.
A
B
C
D
矩形的判定
例1 如图,在 ABCD中,对角线AC、BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
解:∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD= BD
又OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,∴∠BAD=90°
又∠OAD=50°,∴∠OAB=40°
平行四边形的判定
练一练 1.下列判定矩形的说法是否正确?为什么?
(1)有一个角是直角的四边形是矩形.( )
(2)四个角都相等的四边形是矩形.( )
(3)对角线相等的四边形是矩形.( )
×
√
×
03
巩固练习
巩固练习
1.八年级(3)班同学要在广场上布置一个矩形的花坛,计划用红花摆成两条对角线.如果一条对角线用了38盆红花,还需要从花房运来多少盆红花?为什么?如果一条对角线用了49盆呢?
巩固练习
解:还需要从花房运来38盆“红花”.
因为,矩形的对角线相等,所以另一条对角线也需38盆“红花”.且不应除去两条对角线的交点,这是因为38盆是偶数,因此对较线的交点没有摆花盆.
如果一条对角线用了49盆,那么应从花房运来48盆“红花”.因为矩形的对角线相等,但由于49盆是奇数,因此对角线交点应已摆放花盆,所以,另一条对角线上的花盆数应少1盆.
巩固练习
2.如图,平行四边形 ABCD的对角线AC、BD相交于点O,△OAB是等边三角形,且AB=4. 求 平行四边形ABCD的面积.
解:∵△OAB是等边三角形且平行四边形 ABCD的对角线AC、BD互相平分
∴AO=OB=OC=OD=AB=DC=4
∵∠AOB= 60°
∴∠AOD=120°
巩固练习
又∵AO=DO ,
∴∠ADC=90°.
∴四边形ABCD是矩形,
AC=8 ,DC=4, AD=4,
∴矩形ABCD的面积为1.
巩固练习
3.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E,求证:四边形ADCE为矩形.
证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,即∠DAC= ∠BAC.
又∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE= ∠CAM,
巩固练习
∴∠DAE=∠DAC+∠CAE= (∠BAC+∠CAM)=90°.
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形.
巩固练习
4.如图,在四边形ABCD中,AB∥CD,∠BAD=90°,
AB=5,BC=12,AC=13.求证:四边形ABCD是矩形.
证明:四边形ABCD中,AB∥CD,∠BAD=90°,
∴∠ADC=90°.
∵△ABC中,AB=5,BC=12,AC=13,
满足132=52+122,即
∴△ABC是直角三角形,且∠B=90°,
∴四边形ABCD是矩形.
巩固练习
5.如图,在△ABC中,D在AB边上,AD=BD=CD,DE∥AC,DF∥BC.求证:四边形DECF是矩形.
证明:∵AD=BD=CD,
∴△ABC为直角三角形,∠FCE=90°
∵DE∥AC,DF∥BC,
∴四边形DECF为平行四边形,
又∵∠FCE=90°,
∴平行四边形DECF是矩形.
04
课堂小结
课堂小结
矩形的判定定理:
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
矩形的定义:
有一个角是直角的平行四边形是矩形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
