2022—2023学年北师大版数学九年级下册 3.4.1圆周角定理 课时作业(含答案)
文档属性
| 名称 | 2022—2023学年北师大版数学九年级下册 3.4.1圆周角定理 课时作业(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 205.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 07:59:03 | ||
图片预览


文档简介
九年级数学下册课时作业(北师版)
第三章 圆
4 圆周角和圆心角的关系
第1课时 圆周角定理
一、选择题
1.如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是( )
A.75° B.60° C.45° D.30°
2.如图,A,D是⊙O上的两个点,BC是直径.若∠D=32°,则∠OAC的度数是( )
A.64° B.58° C.72° D.55°
3.如图,AB是半圆直径,∠BAC=20°,D是的中点,则∠DAC的度数是( )
A.30° B.35° C.45° D.70°
4.如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为cm,则弦CD的长为( )
A.cm B.3cm C.2cm D.9cm
5.如图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠CDE的度数是50°,则∠A的度数是( )
A.25° B.30° C.40° D.50°
6.如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足为D,E,∠DCE=40°,则∠P的度数为( )
A.140° B.70° C.60° D.40°
7.圆上三点A,B,C把圆分成,,,三条弧的度数之比为1∶2∶3,连AB,BC,CA,则△ABC为( )
A.锐角三角形 B.钝角三角形 C.等腰三角形 D.直角三角形
8.如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B的度数是( )
A.100° B.72° C.64° D.36°
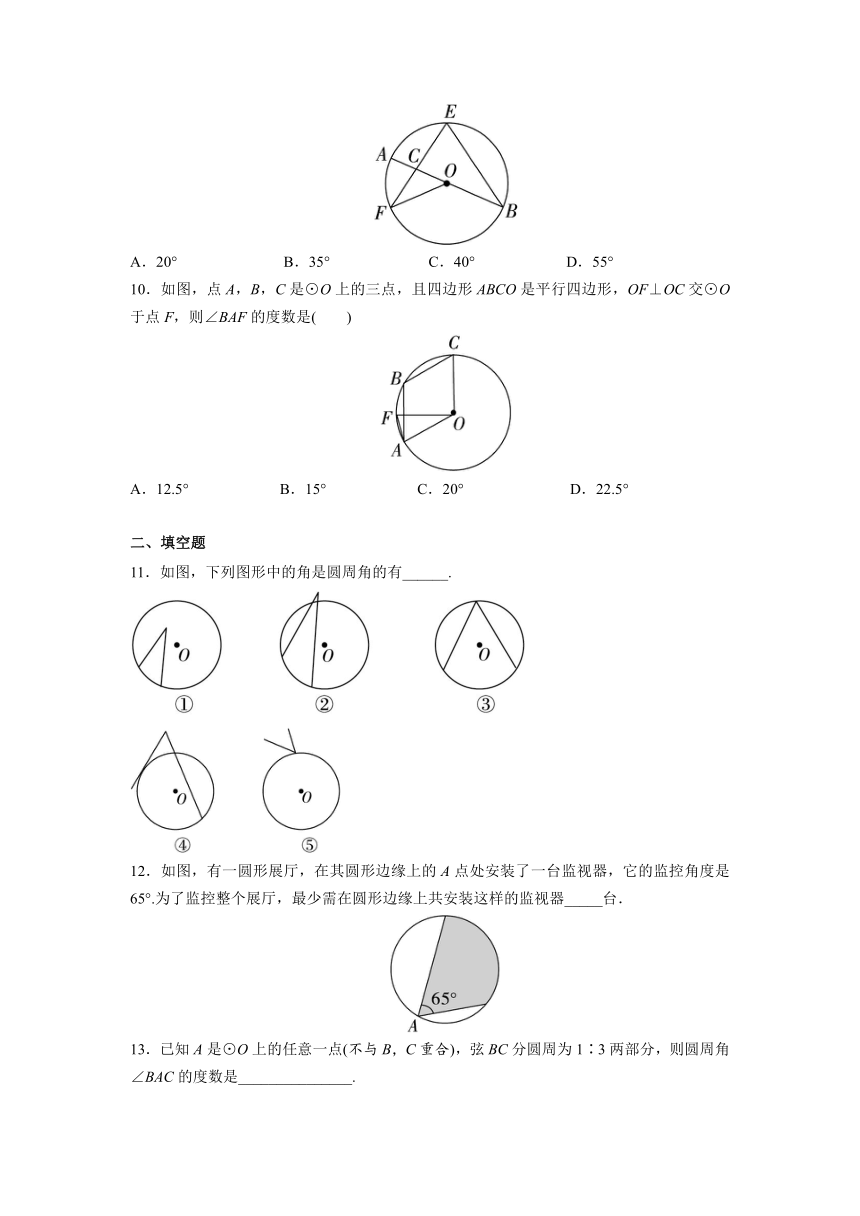
9.如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠F的度数是( )
A.20° B.35° C.40° D.55°
10.如图,点A,B,C是⊙O上的三点,且四边形ABCO是平行四边形,OF⊥OC交⊙O于点F,则∠BAF的度数是( )
A.12.5° B.15° C.20° D.22.5°
二、填空题
11.如图,下列图形中的角是圆周角的有______.
12.如图,有一圆形展厅,在其圆形边缘上的A点处安装了一台监视器,它的监控角度是65°.为了监控整个展厅,最少需在圆形边缘上共安装这样的监视器_____台.
13.已知A是⊙O上的任意一点(不与B,C重合),弦BC分圆周为1∶3两部分,则圆周角∠BAC的度数是_______________.
14.如图,一副三角板ABC和DEF的顶点都在同一个圆上,边DE⊥边BC,则与的度数和是_________.
15.如图,CD是⊙O的直径,若AB⊥CD,垂足为B,∠OAB=40°,则∠C=______.
16.如图,在⊙O中,弦AC=2,点B是圆上一点,且∠ABC=45°,则⊙O的半径是______.
三、解答题
17.如图,在⊙O中,∠AOC=150°,求∠ABC,∠ADC,∠EBC的度数,并判断∠ABC和∠ADC,∠EBC和∠ADC之间的度数关系.
18.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)点P是上一点(不与点C,D重合),求证:∠CPD=∠COB.
(2)点P′在劣弧CD上(不与C,D重合)时,∠CP′D与∠COB之间有什么数量关系?请证明你的结论.
参 考 答 案
1. D 2. B 3. B 4. B 5. A 6. B 7. D 8. C 9. B 10. B
11. ③
12. 3
13. 45°或135°
14. 150°
15. 25°
16.
17. 解:∵∠AOC=150°,∴∠ABC=∠AOC=75°.∵∠α=360°-∠AOC=360°-150°=210°,∴∠ADC=∠α=105°.∵∠EBC=180°-∠ABC=180°-75°=105°,∴∠EBC=∠ADC,即∠EBC与∠ADC相等.又∵∠ABC+∠ADC=75°+105°=180°,∴∠ABC和∠ADC互补.
18. (1)证明:连接OD.∵AB是直径,AB⊥CD.∴=,∴∠COB=∠DOB=∠COD.又∵∠CPD=∠COD,∴∠CPD=∠COB.
(2)解:∠CP′D与∠COB的数量关系是∠CP′D+∠COB=180°.证明:∵点P在优弧CAD上,点P′在劣弧CD上,∴∠CPD+∠CP′D=×360°=180°.由(1)知∠CPD=∠COB,∴∠CP′D+∠COB=180°.
第三章 圆
4 圆周角和圆心角的关系
第1课时 圆周角定理
一、选择题
1.如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是( )
A.75° B.60° C.45° D.30°
2.如图,A,D是⊙O上的两个点,BC是直径.若∠D=32°,则∠OAC的度数是( )
A.64° B.58° C.72° D.55°
3.如图,AB是半圆直径,∠BAC=20°,D是的中点,则∠DAC的度数是( )
A.30° B.35° C.45° D.70°
4.如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为cm,则弦CD的长为( )
A.cm B.3cm C.2cm D.9cm
5.如图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠CDE的度数是50°,则∠A的度数是( )
A.25° B.30° C.40° D.50°
6.如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足为D,E,∠DCE=40°,则∠P的度数为( )
A.140° B.70° C.60° D.40°
7.圆上三点A,B,C把圆分成,,,三条弧的度数之比为1∶2∶3,连AB,BC,CA,则△ABC为( )
A.锐角三角形 B.钝角三角形 C.等腰三角形 D.直角三角形
8.如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B的度数是( )
A.100° B.72° C.64° D.36°
9.如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠F的度数是( )
A.20° B.35° C.40° D.55°
10.如图,点A,B,C是⊙O上的三点,且四边形ABCO是平行四边形,OF⊥OC交⊙O于点F,则∠BAF的度数是( )
A.12.5° B.15° C.20° D.22.5°
二、填空题
11.如图,下列图形中的角是圆周角的有______.
12.如图,有一圆形展厅,在其圆形边缘上的A点处安装了一台监视器,它的监控角度是65°.为了监控整个展厅,最少需在圆形边缘上共安装这样的监视器_____台.
13.已知A是⊙O上的任意一点(不与B,C重合),弦BC分圆周为1∶3两部分,则圆周角∠BAC的度数是_______________.
14.如图,一副三角板ABC和DEF的顶点都在同一个圆上,边DE⊥边BC,则与的度数和是_________.
15.如图,CD是⊙O的直径,若AB⊥CD,垂足为B,∠OAB=40°,则∠C=______.
16.如图,在⊙O中,弦AC=2,点B是圆上一点,且∠ABC=45°,则⊙O的半径是______.
三、解答题
17.如图,在⊙O中,∠AOC=150°,求∠ABC,∠ADC,∠EBC的度数,并判断∠ABC和∠ADC,∠EBC和∠ADC之间的度数关系.
18.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)点P是上一点(不与点C,D重合),求证:∠CPD=∠COB.
(2)点P′在劣弧CD上(不与C,D重合)时,∠CP′D与∠COB之间有什么数量关系?请证明你的结论.
参 考 答 案
1. D 2. B 3. B 4. B 5. A 6. B 7. D 8. C 9. B 10. B
11. ③
12. 3
13. 45°或135°
14. 150°
15. 25°
16.
17. 解:∵∠AOC=150°,∴∠ABC=∠AOC=75°.∵∠α=360°-∠AOC=360°-150°=210°,∴∠ADC=∠α=105°.∵∠EBC=180°-∠ABC=180°-75°=105°,∴∠EBC=∠ADC,即∠EBC与∠ADC相等.又∵∠ABC+∠ADC=75°+105°=180°,∴∠ABC和∠ADC互补.
18. (1)证明:连接OD.∵AB是直径,AB⊥CD.∴=,∴∠COB=∠DOB=∠COD.又∵∠CPD=∠COD,∴∠CPD=∠COB.
(2)解:∠CP′D与∠COB的数量关系是∠CP′D+∠COB=180°.证明:∵点P在优弧CAD上,点P′在劣弧CD上,∴∠CPD+∠CP′D=×360°=180°.由(1)知∠CPD=∠COB,∴∠CP′D+∠COB=180°.
