2022-2023学年人教版八年级数学下册18.2 特殊的平行四边形 课时训练(含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学下册18.2 特殊的平行四边形 课时训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 227.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 08:03:25 | ||
图片预览

文档简介
18.2 特殊的平行四边形 课时训练-2022-2023学年人教版八年级数学下册
一、单选题
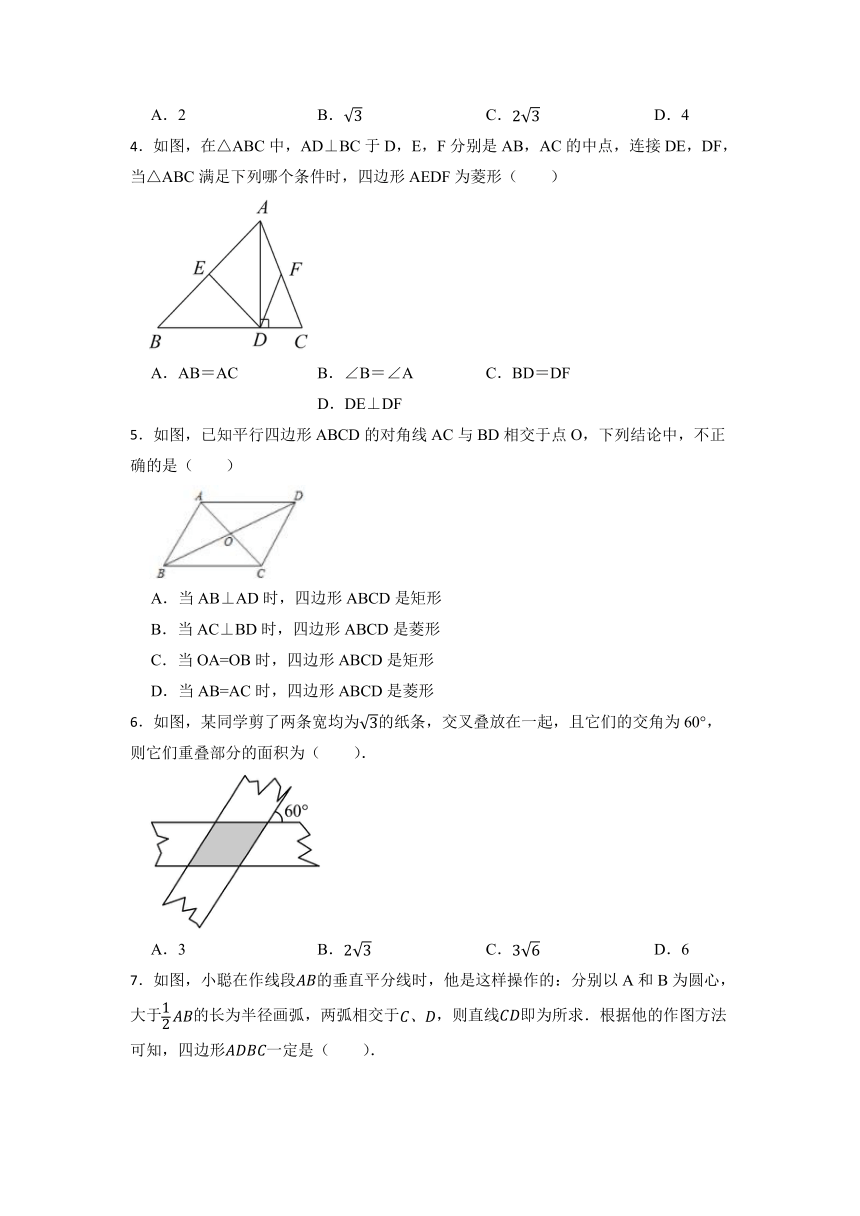
1.如图,在中,,AD是角平分线,且,,点E为中点,则的值为( )
A.5 B.5.8 C.6 D.6.5
2.已知8个长为a,宽为b的小长方形(如图1),不重叠无空隙地摆放(如图2),在长方形ABCD中,当BC长度变化时,左上角阴影面积与右下角阴影面积的差没有变化,则a,b之间的关系应满足( )
A. B. C. D.
3.如图,长方形纸片中, 点是的中点,连接; 按以下步骤作图:①分别 以点和为圆心, 以大于的等长为半径作弧,两弧相交于点和;②作直线,且直线刚好经过点.若,则的长度是( )
A.2 B. C. D.4
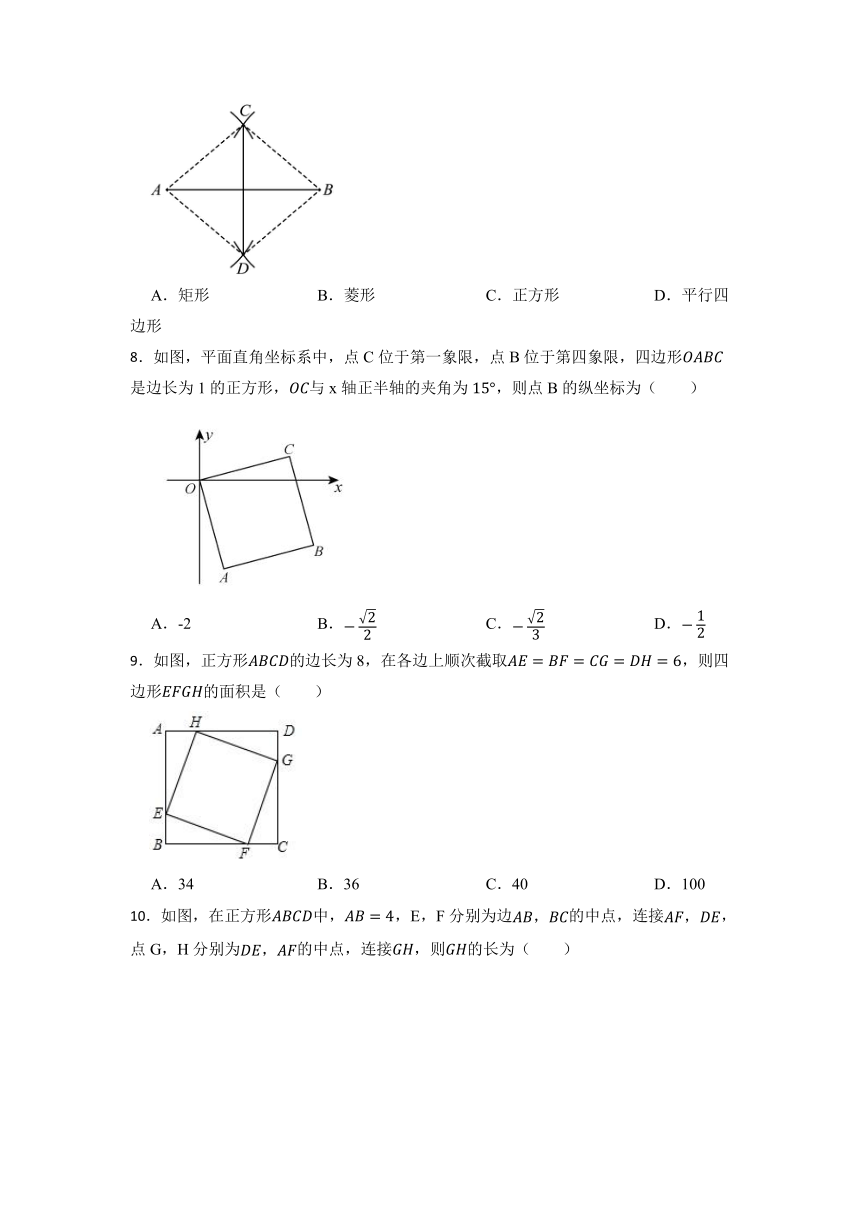
4.如图,在△ABC中,AD⊥BC于D,E,F分别是AB,AC的中点,连接DE,DF,当△ABC满足下列哪个条件时,四边形AEDF为菱形( )
A.AB=AC B.∠B=∠A C.BD=DF D.DE⊥DF
5.如图,已知平行四边形ABCD的对角线AC与BD相交于点O,下列结论中,不正确的是( )
A.当AB⊥AD时,四边形ABCD是矩形
B.当AC⊥BD时,四边形ABCD是菱形
C.当OA=OB时,四边形ABCD是矩形
D.当AB=AC时,四边形ABCD是菱形
6.如图,某同学剪了两条宽均为的纸条,交叉叠放在一起,且它们的交角为60°,则它们重叠部分的面积为( ).
A.3 B. C. D.6
7.如图,小聪在作线段的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于的长为半径画弧,两弧相交于,则直线即为所求.根据他的作图方法可知,四边形一定是( ).
A.矩形 B.菱形 C.正方形 D.平行四边形
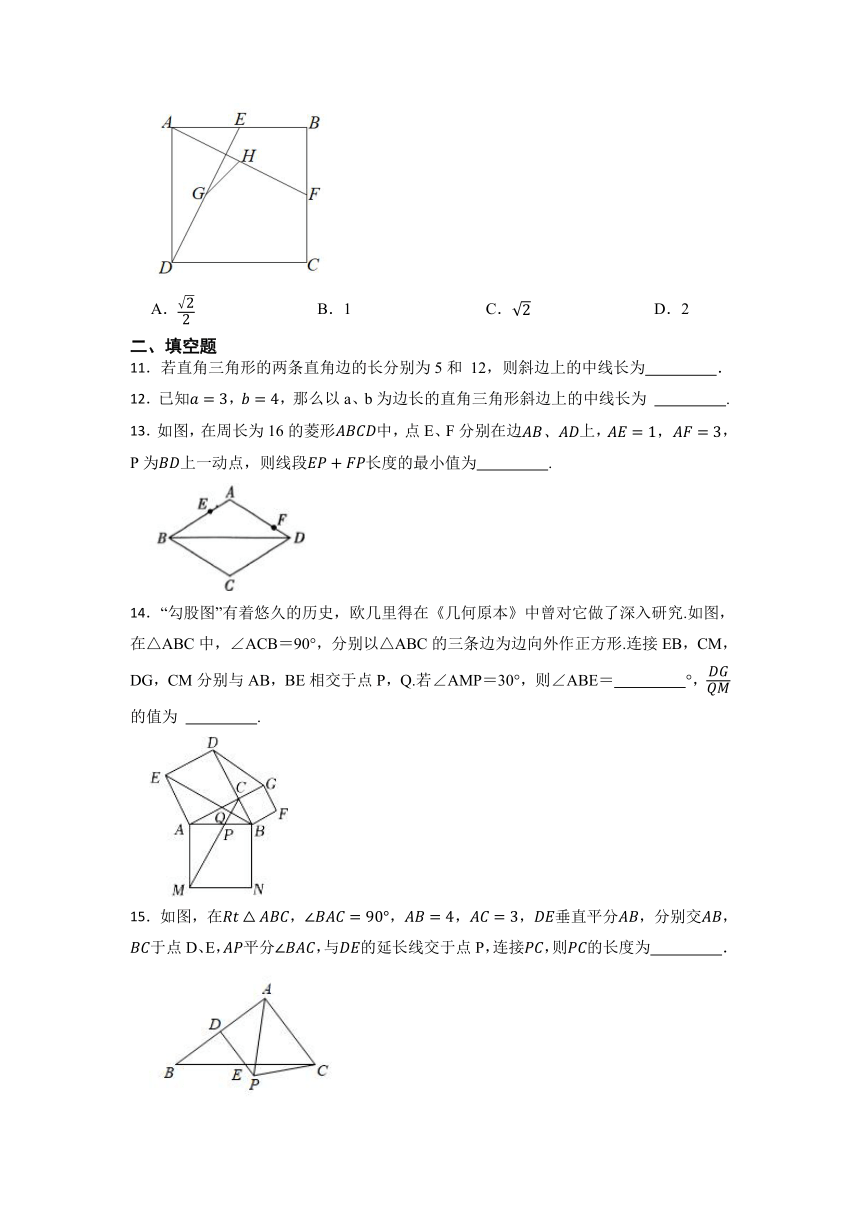
8.如图,平面直角坐标系中,点C位于第一象限,点B位于第四象限,四边形是边长为1的正方形,与x轴正半轴的夹角为,则点B的纵坐标为( )
A.-2 B. C. D.
9.如图,正方形的边长为8,在各边上顺次截取,则四边形的面积是( )
A.34 B.36 C.40 D.100
10.如图,在正方形中,,E,F分别为边的中点,连接,点G,H分别为的中点,连接,则的长为( )
A. B.1 C. D.2
二、填空题
11.若直角三角形的两条直角边的长分别为5和 12,则斜边上的中线长为 .
12.已知,,那么以a、b为边长的直角三角形斜边上的中线长为 .
13.如图,在周长为16的菱形中,点E、F分别在边上,,P为上一动点,则线段长度的最小值为 .
14.“勾股图”有着悠久的历史,欧几里得在《几何原本》中曾对它做了深入研究.如图,在△ABC中,∠ACB=90°,分别以△ABC的三条边为边向外作正方形.连接EB,CM,DG,CM分别与AB,BE相交于点P,Q.若∠AMP=30°,则∠ABE= °,的值为 .
15.如图,在,,,,垂直平分,分别交,于点D、E,平分,与的延长线交于点P,连接,则的长度为 .
三、解答题
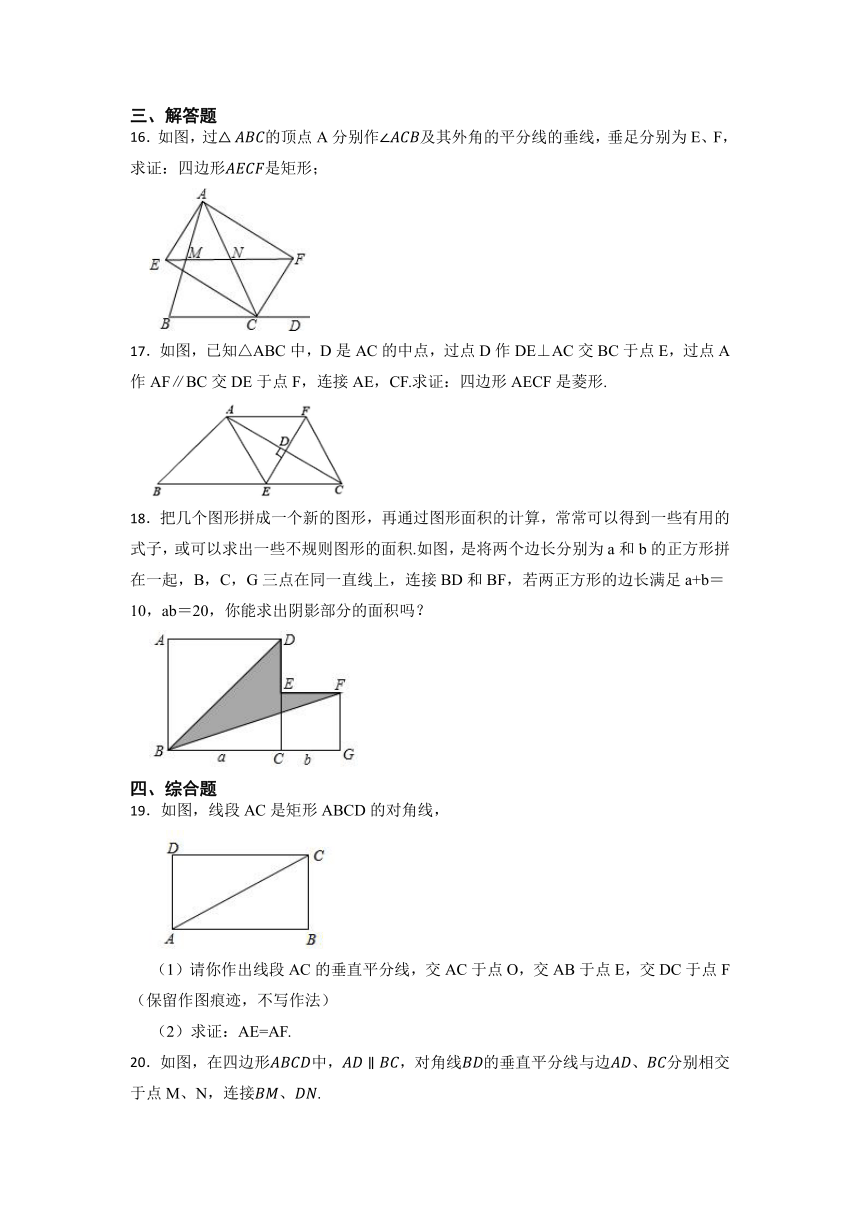
16.如图,过的顶点A分别作及其外角的平分线的垂线,垂足分别为E、F,求证:四边形是矩形;
17.如图,已知△ABC中,D是AC的中点,过点D作DE⊥AC交BC于点E,过点A作AF∥BC交DE于点F,连接AE,CF.求证:四边形AECF是菱形.
18.把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.如图,是将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=10,ab=20,你能求出阴影部分的面积吗?
四、综合题
19.如图,线段AC是矩形ABCD的对角线,
(1)请你作出线段AC的垂直平分线,交AC于点O,交AB于点E,交DC于点F(保留作图痕迹,不写作法)
(2)求证:AE=AF.
20.如图,在四边形中,,对角线的垂直平分线与边、分别相交于点M、N,连接、.
(1)求证:四边形是菱形;
(2)若四边形的周长为52,,求的长.
21.如图,已知在菱形中,对角线与交于点,延长到点,使,延长到点,使,顺次连接点,若,.
(1)求证:四边形是矩形;
(2)求四边形的周长为多少.
22.如图,E是正方形ABCD对角线BD上一点,连接AE,CE,并延长CE交AD于点F.
(1)求证:△ABE≌△CBE;
(2)若∠AEC=140°,求∠DFE的度数.
23.如图1,在中,,D是的中点,点E在线段上,连结,作交直线于点F,连结.
(1)【初步尝试】
如图2,当,线段的长度是 ,线段的长度是 .
(2)【结论探究】
如图1,小宁猜想“”,但她未能想出证明思路,小波介绍了添加辅助线的方法,如下表所示,请帮小宁完成证明.
如图,延长至G,使,连结,.
(3)【拓展应用】
如图3,当点E在线段的延长线上时,连结,作交直线于点F,连结.请补全图形,并求出当时,线段的长.
答案解析部分
1.【答案】A
2.【答案】B
3.【答案】C
4.【答案】A
5.【答案】D
6.【答案】B
7.【答案】B
8.【答案】B
9.【答案】C
10.【答案】C
11.【答案】6.5
12.【答案】2或2.5
13.【答案】4
14.【答案】30;
15.【答案】
16.【答案】证明:∵平分,平分,
∴,,
∵,
∴,
即,
又∵,,
∴,
∴四边形是矩形.
17.【答案】证明:在△ABC中,点D是AC的中点,
∴AD=DC,
∵AF∥BC,
∴∠FAD=∠ECD,∠AFD=∠CED,
∴△AFD≌△CED(AAS),
∴AF=EC,
又∵AF∥BC,
∴四边形AECF是平行四边形,
又∵DE⊥AC,
∴EF⊥AC
∴平行四边形AECF是菱形.
18.【答案】解:∵a+b=10,ab=20,
∴(a+b)2=100,
∴a2+b2+2ab=100,
∴a2+b2=60,
∴S阴影=S两正方形﹣S△ABD﹣S△BFG
=a2+b2﹣ a2﹣b(a+b)
=(a2+b2﹣ab)
=×(60﹣20)
=20.
19.【答案】(1)解:如图:
(2)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠OCF=∠OAE,
在△OCF和△OAE中,
,
∴△COF≌△AOE(ASA),
∴AE=CF,
∵EF是AC的垂直平分线,
∴AF=CF,
∴AE=AF.
20.【答案】(1)证明:∵,
∴.
∵直线是对角线的垂直平分线,
∴,.
在和中,
,
∴,
∴,
∵,
∴四边形是平行四边形,
∵,
∴四边形是菱形;
(2)解:∵菱形的周长为52,
∴,
又∵,
∴
在中,由勾股定理得,
∴,
∴.
21.【答案】(1)证明:∵四边形是菱形,
∴,
∵,
∴四边形是平行四边形,
∵,,
∴是的中位线,
∴,
∴,
∴,
∴平行四边形是矩形;
(2)解:∵四边形是菱形,
∴,
由(1)可知,是的中位线,,
∴,
∵四边形是矩形,,
∴,,
∴四边形的周长.
22.【答案】(1)证明:∵四边形ABCD是正方形,
∴AB=CB,∠ABC=∠ADC=90°,∠ABE=∠CBE=45°,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS);
(2)解:∵△ABE≌△CBE,
∴∠AEB=∠CEB,
又∵∠AEC=140°,
∴∠CEB=70°,
∵∠DEC+∠CEB=180°,
∴∠DEC=180°﹣∠CEB=110°,
∵∠DFE+∠ADB=∠DEC,
∴∠DFE=∠DEC﹣∠ADB=110°﹣45°=65°.
23.【答案】(1)5;3
(2)解:延长至G,使,连结,,
∵D是中点,
∴,
在和中
,
∴,
∴,
∵,
∴,即,
∵,
∴是的垂直平分线,
∴,
在中,,
∴.
(3)解:延长至G,使,连接,,
由(2)同理可证
∴
∴,
∴,
∴
∵,
∴,
∴
设,则,
∵,
∴,
在中,,
∵,
∴
解得,;
∴.
一、单选题
1.如图,在中,,AD是角平分线,且,,点E为中点,则的值为( )
A.5 B.5.8 C.6 D.6.5
2.已知8个长为a,宽为b的小长方形(如图1),不重叠无空隙地摆放(如图2),在长方形ABCD中,当BC长度变化时,左上角阴影面积与右下角阴影面积的差没有变化,则a,b之间的关系应满足( )
A. B. C. D.
3.如图,长方形纸片中, 点是的中点,连接; 按以下步骤作图:①分别 以点和为圆心, 以大于的等长为半径作弧,两弧相交于点和;②作直线,且直线刚好经过点.若,则的长度是( )
A.2 B. C. D.4
4.如图,在△ABC中,AD⊥BC于D,E,F分别是AB,AC的中点,连接DE,DF,当△ABC满足下列哪个条件时,四边形AEDF为菱形( )
A.AB=AC B.∠B=∠A C.BD=DF D.DE⊥DF
5.如图,已知平行四边形ABCD的对角线AC与BD相交于点O,下列结论中,不正确的是( )
A.当AB⊥AD时,四边形ABCD是矩形
B.当AC⊥BD时,四边形ABCD是菱形
C.当OA=OB时,四边形ABCD是矩形
D.当AB=AC时,四边形ABCD是菱形
6.如图,某同学剪了两条宽均为的纸条,交叉叠放在一起,且它们的交角为60°,则它们重叠部分的面积为( ).
A.3 B. C. D.6
7.如图,小聪在作线段的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于的长为半径画弧,两弧相交于,则直线即为所求.根据他的作图方法可知,四边形一定是( ).
A.矩形 B.菱形 C.正方形 D.平行四边形
8.如图,平面直角坐标系中,点C位于第一象限,点B位于第四象限,四边形是边长为1的正方形,与x轴正半轴的夹角为,则点B的纵坐标为( )
A.-2 B. C. D.
9.如图,正方形的边长为8,在各边上顺次截取,则四边形的面积是( )
A.34 B.36 C.40 D.100
10.如图,在正方形中,,E,F分别为边的中点,连接,点G,H分别为的中点,连接,则的长为( )
A. B.1 C. D.2
二、填空题
11.若直角三角形的两条直角边的长分别为5和 12,则斜边上的中线长为 .
12.已知,,那么以a、b为边长的直角三角形斜边上的中线长为 .
13.如图,在周长为16的菱形中,点E、F分别在边上,,P为上一动点,则线段长度的最小值为 .
14.“勾股图”有着悠久的历史,欧几里得在《几何原本》中曾对它做了深入研究.如图,在△ABC中,∠ACB=90°,分别以△ABC的三条边为边向外作正方形.连接EB,CM,DG,CM分别与AB,BE相交于点P,Q.若∠AMP=30°,则∠ABE= °,的值为 .
15.如图,在,,,,垂直平分,分别交,于点D、E,平分,与的延长线交于点P,连接,则的长度为 .
三、解答题
16.如图,过的顶点A分别作及其外角的平分线的垂线,垂足分别为E、F,求证:四边形是矩形;
17.如图,已知△ABC中,D是AC的中点,过点D作DE⊥AC交BC于点E,过点A作AF∥BC交DE于点F,连接AE,CF.求证:四边形AECF是菱形.
18.把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.如图,是将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=10,ab=20,你能求出阴影部分的面积吗?
四、综合题
19.如图,线段AC是矩形ABCD的对角线,
(1)请你作出线段AC的垂直平分线,交AC于点O,交AB于点E,交DC于点F(保留作图痕迹,不写作法)
(2)求证:AE=AF.
20.如图,在四边形中,,对角线的垂直平分线与边、分别相交于点M、N,连接、.
(1)求证:四边形是菱形;
(2)若四边形的周长为52,,求的长.
21.如图,已知在菱形中,对角线与交于点,延长到点,使,延长到点,使,顺次连接点,若,.
(1)求证:四边形是矩形;
(2)求四边形的周长为多少.
22.如图,E是正方形ABCD对角线BD上一点,连接AE,CE,并延长CE交AD于点F.
(1)求证:△ABE≌△CBE;
(2)若∠AEC=140°,求∠DFE的度数.
23.如图1,在中,,D是的中点,点E在线段上,连结,作交直线于点F,连结.
(1)【初步尝试】
如图2,当,线段的长度是 ,线段的长度是 .
(2)【结论探究】
如图1,小宁猜想“”,但她未能想出证明思路,小波介绍了添加辅助线的方法,如下表所示,请帮小宁完成证明.
如图,延长至G,使,连结,.
(3)【拓展应用】
如图3,当点E在线段的延长线上时,连结,作交直线于点F,连结.请补全图形,并求出当时,线段的长.
答案解析部分
1.【答案】A
2.【答案】B
3.【答案】C
4.【答案】A
5.【答案】D
6.【答案】B
7.【答案】B
8.【答案】B
9.【答案】C
10.【答案】C
11.【答案】6.5
12.【答案】2或2.5
13.【答案】4
14.【答案】30;
15.【答案】
16.【答案】证明:∵平分,平分,
∴,,
∵,
∴,
即,
又∵,,
∴,
∴四边形是矩形.
17.【答案】证明:在△ABC中,点D是AC的中点,
∴AD=DC,
∵AF∥BC,
∴∠FAD=∠ECD,∠AFD=∠CED,
∴△AFD≌△CED(AAS),
∴AF=EC,
又∵AF∥BC,
∴四边形AECF是平行四边形,
又∵DE⊥AC,
∴EF⊥AC
∴平行四边形AECF是菱形.
18.【答案】解:∵a+b=10,ab=20,
∴(a+b)2=100,
∴a2+b2+2ab=100,
∴a2+b2=60,
∴S阴影=S两正方形﹣S△ABD﹣S△BFG
=a2+b2﹣ a2﹣b(a+b)
=(a2+b2﹣ab)
=×(60﹣20)
=20.
19.【答案】(1)解:如图:
(2)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠OCF=∠OAE,
在△OCF和△OAE中,
,
∴△COF≌△AOE(ASA),
∴AE=CF,
∵EF是AC的垂直平分线,
∴AF=CF,
∴AE=AF.
20.【答案】(1)证明:∵,
∴.
∵直线是对角线的垂直平分线,
∴,.
在和中,
,
∴,
∴,
∵,
∴四边形是平行四边形,
∵,
∴四边形是菱形;
(2)解:∵菱形的周长为52,
∴,
又∵,
∴
在中,由勾股定理得,
∴,
∴.
21.【答案】(1)证明:∵四边形是菱形,
∴,
∵,
∴四边形是平行四边形,
∵,,
∴是的中位线,
∴,
∴,
∴,
∴平行四边形是矩形;
(2)解:∵四边形是菱形,
∴,
由(1)可知,是的中位线,,
∴,
∵四边形是矩形,,
∴,,
∴四边形的周长.
22.【答案】(1)证明:∵四边形ABCD是正方形,
∴AB=CB,∠ABC=∠ADC=90°,∠ABE=∠CBE=45°,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS);
(2)解:∵△ABE≌△CBE,
∴∠AEB=∠CEB,
又∵∠AEC=140°,
∴∠CEB=70°,
∵∠DEC+∠CEB=180°,
∴∠DEC=180°﹣∠CEB=110°,
∵∠DFE+∠ADB=∠DEC,
∴∠DFE=∠DEC﹣∠ADB=110°﹣45°=65°.
23.【答案】(1)5;3
(2)解:延长至G,使,连结,,
∵D是中点,
∴,
在和中
,
∴,
∴,
∵,
∴,即,
∵,
∴是的垂直平分线,
∴,
在中,,
∴.
(3)解:延长至G,使,连接,,
由(2)同理可证
∴
∴,
∴,
∴
∵,
∴,
∴
设,则,
∵,
∴,
在中,,
∵,
∴
解得,;
∴.
