2022-2023学年人教版八年级数学下册20.2 数据的波动程度 课时训练(含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学下册20.2 数据的波动程度 课时训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 68.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 08:18:05 | ||
图片预览



文档简介
20.2 数据的波动程度 课时训练-2022-2023学年人教版八年级数学下册
一、单选题
1.有甲、乙两组数据,如下表所示:
甲 11 12 13 14 15
乙 12 12 13 14 14
两组数据的方差分别是、,则与的大小关系为( )
A. B. C. D.
2.在方差的计算公式中,数字10和20表示的意义分别是( )
A.数据得个数和平均数 B.数据的方差和平均数
C.数个数和方差 D.以上都不对
3.若x1,x2,x3, ,xn的平均数为8,方差为2,则关于x1+2,x2+2,x3+2,……,xn+2,下列结论正确的是( )
A.平均数为8,方差为2 B.平均数为8,方差为4
C.平均数为10,方差为2 D.平均数为10,方差为4
4.为了从四名同学中选出一人参加计算机编程比赛,对他们进行了多次测试,并对每个人的测试成绩的平均数及方差进行了统计(如下表),则应选的同学是( )
学生 学生一 学生二 学生三 学生四
平均数 95 96 96 95
方差 5 5 4.8 4.8
A.学生一 B.学生二 C.学生三 D.学生四
5.为备战2024年巴黎奥运会,甲、乙两名运动员训练测验,两名运动员的平均分相同,且,,则成绩较稳定的是( )
A.乙运动员 B.甲运动员
C.两运动员一样稳定 D.无法确定
6.甲、乙、丙、丁四位同学3次数学成绩的平均分都是120分,方差分别是,,,.则这四位同学3次数学成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
7.某校将举办一场“中国汉字听写大赛”,要求各班推选一名同学参加比赛,为此,八年二班组织了五轮班级选拔赛,在这五轮选拔赛中,甲、乙两位同学的平均分都是97分,甲的成绩的方差是0.3,乙的成绩的方差是0.7.根据以上数据,下列说法正确的是( )
A.甲的成绩比乙的成绩稳定
B.乙的成绩比甲的成绩稳定
C.甲、乙两人的成绩一样稳定
D.无法确定甲、乙的成绩谁更稳定
8.甲组数据为4、5、6、7;乙组数据为3、5、6、8,下列说法正确的是( )
A.甲更稳定 B.乙更稳定 C.方差一样 D.无法比较
9.某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们亩产量的平均数分别是千克,千克,方差分别是,.则关于这两种小麦推广种植的合理决策是( )
A.乙的平均亩产量较高,应推广乙
B.甲、乙的平均亩产量相差不多,均可推广
C.甲、乙的平均亩产量相差不多,但甲的亩产量比较稳定,应推广甲
D.乙的平均亩产量较高,且亩产量比较稳定,应推广乙
10.若一组数据x1,x2,…xn的平均数为17,方差为2,则另一组数据x1+1,x2+1,…,xn+1的平均数、方差分别为( )
A.17,2 B.18,2 C.17,3 D.18,3
二、填空题
11.某校要从甲、乙两名同学中选取一名成绩稳定的同学去参加数学竞赛,已知五次模拟测试中统计所得的信息为=115,S甲2=12,=115,S乙2=36,则应选择 参加竞赛.
12.“共和国勋章”获得者、“杂交水稻之父”袁隆平为世界粮食安全作出了杰出贡献.全球共有40多个国家引种杂交水稻,中国境外种植面积达800万公顷.某村引进了甲、乙两种超级杂交水稻品种,在条件(肥力、日照、通风……)不同的6块试验田中同时播种并核定亩产,统计结果为:/亩,﹐/亩,,则 品种更适合在该村推广.(填“甲”或“乙”)
13.数据的平均数是4,方差是3,则数据的平均数和方差分别是 , .
14.在一次舞蹈比赛中,甲、乙两队人数相同,身高的平均数相同,方差分别为:,,则这两队队员身高最整齐的是 .
15.下表记录了甲、乙、丙三名学生这学期的射击成绩的平均数和方差
甲 乙 丙
平均数 9.23 9.3 9.3
方差 0.23 0.017 0.057
根据表中的数据,要选择一名成绩好且发挥稳定的学生参加比赛,应选择 .
三、解答题
16.某学校为选拔数学能力突出的学生参加中学生数学竞赛,组织了多次测试,其中甲乙两位同学成绩较为优秀,他们在六次赛前测试中的成绩(单位:分)如下表所示.
甲 80 75 90 64 88 95
乙 84 80 88 76 79 85
如果根据这六次成绩选拔其中一人参加比赛,你认为哪一位比较合适?为什么?
17.为了选拔一名学生参加全市诗词大赛,学校组织了四次测试,其中甲乙两位同学成绩较为优秀,他们在四次测试中的成绩(单位:分)如表所示:
甲 90 85 95 90
乙 98 82 88 92
通过计算,甲同学在这四次测试中的平均分为90分,分别求出两位同学测试成绩的方差.从成绩稳定性的角度出发,你认为选谁参加比赛较合适?
18.2018年12月4日是第五个国家宪法日,也是第一个“宪法宣传周”.甲、乙两班各选派10名学生参加宪法知识竞赛(满分100分),成绩如下:
成绩 85 90 95 100
甲班参赛学生/人 1 1 5 3
乙班参赛学生/人 1 2 3 4
分别求甲、乙两班参赛学生竞赛成绩的平均数和方差.
四、综合题
19.某学校组织七、八年级全体学生举行了安全知识竞赛活动,为了解竞赛成绩情况,为两个年级各随机抽取10名学生的成绩(满分为100分)进行了分析,并依据分析结果绘制了如下表所示的不完整统计表:
七年级:90,95,95,80,85,90,80,90,85,100;
八年级:85,85,95,80,95,90,90,90,100,90.
年级 平均数 中位数 众数 方差
七年级 89 m 90 39
八年级 n 90 p q
根据以上信息解答下面问题:
(1)填空:m= ,p= ;
(2)求q的值;
(3)通过数据分析,你认为哪个年级的成绩比较好?说明理由.
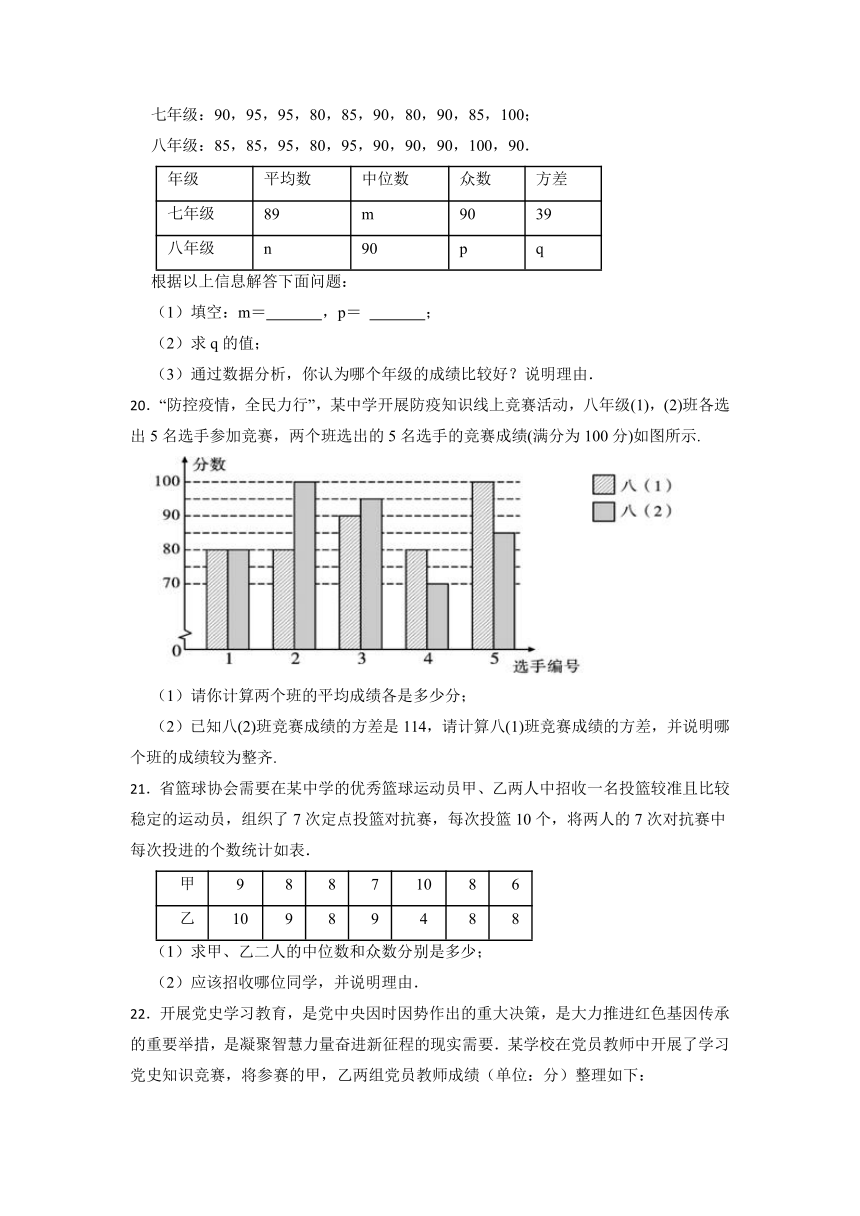
20.“防控疫情,全民力行”,某中学开展防疫知识线上竞赛活动,八年级(1),(2)班各选出5名选手参加竞赛,两个班选出的5名选手的竞赛成绩(满分为100分)如图所示.
(1)请你计算两个班的平均成绩各是多少分;
(2)已知八(2)班竞赛成绩的方差是114,请计算八(1)班竞赛成绩的方差,并说明哪个班的成绩较为整齐.
21.省篮球协会需要在某中学的优秀篮球运动员甲、乙两人中招收一名投篮较准且比较稳定的运动员,组织了7次定点投篮对抗赛,每次投篮10个,将两人的7次对抗赛中每次投进的个数统计如表.
甲 9 8 8 7 10 8 6
乙 10 9 8 9 4 8 8
(1)求甲、乙二人的中位数和众数分别是多少;
(2)应该招收哪位同学,并说明理由.
22.开展党史学习教育,是党中央因时因势作出的重大决策,是大力推进红色基因传承的重要举措,是凝聚智慧力量奋进新征程的现实需要.某学校在党员教师中开展了学习党史知识竞赛,将参赛的甲,乙两组党员教师成绩(单位:分)整理如下:
整理数据:
甲组:6,6,9,7,9,10,9.
乙组:7,6,10,5,9,9,10.
分析数据:
平均数 中位数 众数
甲组 8 b c
乙组 a 9 9和10
(1)表中的 , , ;
(2)已知甲组教师成绩的方差为,请计算乙组教师成绩的方差,并说明哪组教师的成绩更稳定?
23.2022年4月7日是第73个世界卫生日,某学校为纪念爱国卫生运动以及抗击新冠肺炎疫情决定在八年级举办卫生知识竞赛活动.甲,乙两班各选派5名学生参加学校卫生知识竞赛(满分100分).成绩如下(单位:分):
甲班:96,92,94,97,96;
乙班;90,98,97,98,92.
通过数据分析,列表如下:
班级 平均分 中位数 众数
甲班 a 96 96
乙班 95 b c
(1)填空:a= ,b= ,c= ;
(2)已知乙班学生竞赛成绩的方差为11.2,请计算甲班学生竞赛成绩的方差,并回答哪个班的学生竞赛成绩更稳定?
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】C
4.【答案】C
5.【答案】A
6.【答案】B
7.【答案】A
8.【答案】A
9.【答案】C
10.【答案】B
11.【答案】甲
12.【答案】乙
13.【答案】5;3
14.【答案】乙
15.【答案】乙
16.【答案】解: (分),
(分),
,
,
∵甲的方差大于乙的方差,
∴乙参加比赛比较合适.
17.【答案】解: (分)
∵
∴选择甲参加比赛较合适
18.【答案】解:甲班参赛学生的平均数是: (85×1+90×1+95×5+100×3)=95(分)
乙班参赛学生的平均数是: (85×1+90×2+95×3+100×4)=95(分)
则S甲2= [(85﹣95)2+(90﹣95)2+5(95﹣95)2+3(100﹣95)2]=20(分2)
S乙2= [(85﹣95)2+2(90﹣95)2+3(95﹣95)2+4(100﹣95)2]=25(分2)
答:甲、乙两班参赛学生竞赛成绩的平均数都是95分,方差分别为20分2,25分2.
19.【答案】(1)90|90
(2)解:八年级的平均数n=×(85×2+95×2+90×4+80+100)=90,方差为q=×[2×(85﹣90)2+2×(95﹣90)2+4×(90﹣90)2+(80﹣90)2+(100﹣90)2]=30;
(3)解:从平均分来看八年级高;通过方差来看,八年级的方差小,说明八年级的成绩稳定,所以八年级比较好.
20.【答案】(1)解:八(1)班的成绩分别为80,80,90,80,100;
八(2)班的成绩分别为80,100,95,70,85;
∴八(1)班的平均成绩为分;
八(2)班的平均成绩为分;
答:八(1)班平均成绩为86分,八(2)班平均成绩为86分.
(2)解:八(1)班竞赛成绩的方差为;
∵64<114,
∴八(1)班的成绩较为整齐.
21.【答案】(1)解:将甲的7个数据按照由小到大的顺序排列:6,7,8,8,8,9,10,
在最中间的数是8,8出现了3次,出现次数最多,
∴这组数据的中位数为8,众数为8.
将乙的7个数据按照由小到大的顺序排列:4,8,8,8,9,9,10,
在最中间的数是8,8出现了3次,出现次数最多,
∴这组数据的中位数为8,众数为8.
答:甲、乙二人的中位数和众数分别是8,8,8,8;
(2)解:应该招收甲同学.理由如下:
甲的平均数为.
甲的方差=×[(6-8)2+(7-8)2+3×(8-8)2+(9-8)2+(10-8)2]=,
乙的平均数为.
乙的方差=×[(4-8)2+3×(8-8)2+2×(9-8)2+(10-8)2]=,
∴甲、乙的平均成绩都为8,但甲的方差<乙的方差,
∴在平均数相同的情况下,甲的方差比乙小,故甲比乙稳定,应该招收甲同学.
22.【答案】(1)8;9;9
(2)解:.
,
甲组教师成绩的方差较小,成绩更为稳定.
23.【答案】(1)95;97;98
(2)解:由(1)知甲班同学竞赛成绩的平均分为95,
∴方差为: .
∵11.2>3.2,
∴甲班的学生竞赛成绩更稳定.
一、单选题
1.有甲、乙两组数据,如下表所示:
甲 11 12 13 14 15
乙 12 12 13 14 14
两组数据的方差分别是、,则与的大小关系为( )
A. B. C. D.
2.在方差的计算公式中,数字10和20表示的意义分别是( )
A.数据得个数和平均数 B.数据的方差和平均数
C.数个数和方差 D.以上都不对
3.若x1,x2,x3, ,xn的平均数为8,方差为2,则关于x1+2,x2+2,x3+2,……,xn+2,下列结论正确的是( )
A.平均数为8,方差为2 B.平均数为8,方差为4
C.平均数为10,方差为2 D.平均数为10,方差为4
4.为了从四名同学中选出一人参加计算机编程比赛,对他们进行了多次测试,并对每个人的测试成绩的平均数及方差进行了统计(如下表),则应选的同学是( )
学生 学生一 学生二 学生三 学生四
平均数 95 96 96 95
方差 5 5 4.8 4.8
A.学生一 B.学生二 C.学生三 D.学生四
5.为备战2024年巴黎奥运会,甲、乙两名运动员训练测验,两名运动员的平均分相同,且,,则成绩较稳定的是( )
A.乙运动员 B.甲运动员
C.两运动员一样稳定 D.无法确定
6.甲、乙、丙、丁四位同学3次数学成绩的平均分都是120分,方差分别是,,,.则这四位同学3次数学成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
7.某校将举办一场“中国汉字听写大赛”,要求各班推选一名同学参加比赛,为此,八年二班组织了五轮班级选拔赛,在这五轮选拔赛中,甲、乙两位同学的平均分都是97分,甲的成绩的方差是0.3,乙的成绩的方差是0.7.根据以上数据,下列说法正确的是( )
A.甲的成绩比乙的成绩稳定
B.乙的成绩比甲的成绩稳定
C.甲、乙两人的成绩一样稳定
D.无法确定甲、乙的成绩谁更稳定
8.甲组数据为4、5、6、7;乙组数据为3、5、6、8,下列说法正确的是( )
A.甲更稳定 B.乙更稳定 C.方差一样 D.无法比较
9.某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们亩产量的平均数分别是千克,千克,方差分别是,.则关于这两种小麦推广种植的合理决策是( )
A.乙的平均亩产量较高,应推广乙
B.甲、乙的平均亩产量相差不多,均可推广
C.甲、乙的平均亩产量相差不多,但甲的亩产量比较稳定,应推广甲
D.乙的平均亩产量较高,且亩产量比较稳定,应推广乙
10.若一组数据x1,x2,…xn的平均数为17,方差为2,则另一组数据x1+1,x2+1,…,xn+1的平均数、方差分别为( )
A.17,2 B.18,2 C.17,3 D.18,3
二、填空题
11.某校要从甲、乙两名同学中选取一名成绩稳定的同学去参加数学竞赛,已知五次模拟测试中统计所得的信息为=115,S甲2=12,=115,S乙2=36,则应选择 参加竞赛.
12.“共和国勋章”获得者、“杂交水稻之父”袁隆平为世界粮食安全作出了杰出贡献.全球共有40多个国家引种杂交水稻,中国境外种植面积达800万公顷.某村引进了甲、乙两种超级杂交水稻品种,在条件(肥力、日照、通风……)不同的6块试验田中同时播种并核定亩产,统计结果为:/亩,﹐/亩,,则 品种更适合在该村推广.(填“甲”或“乙”)
13.数据的平均数是4,方差是3,则数据的平均数和方差分别是 , .
14.在一次舞蹈比赛中,甲、乙两队人数相同,身高的平均数相同,方差分别为:,,则这两队队员身高最整齐的是 .
15.下表记录了甲、乙、丙三名学生这学期的射击成绩的平均数和方差
甲 乙 丙
平均数 9.23 9.3 9.3
方差 0.23 0.017 0.057
根据表中的数据,要选择一名成绩好且发挥稳定的学生参加比赛,应选择 .
三、解答题
16.某学校为选拔数学能力突出的学生参加中学生数学竞赛,组织了多次测试,其中甲乙两位同学成绩较为优秀,他们在六次赛前测试中的成绩(单位:分)如下表所示.
甲 80 75 90 64 88 95
乙 84 80 88 76 79 85
如果根据这六次成绩选拔其中一人参加比赛,你认为哪一位比较合适?为什么?
17.为了选拔一名学生参加全市诗词大赛,学校组织了四次测试,其中甲乙两位同学成绩较为优秀,他们在四次测试中的成绩(单位:分)如表所示:
甲 90 85 95 90
乙 98 82 88 92
通过计算,甲同学在这四次测试中的平均分为90分,分别求出两位同学测试成绩的方差.从成绩稳定性的角度出发,你认为选谁参加比赛较合适?
18.2018年12月4日是第五个国家宪法日,也是第一个“宪法宣传周”.甲、乙两班各选派10名学生参加宪法知识竞赛(满分100分),成绩如下:
成绩 85 90 95 100
甲班参赛学生/人 1 1 5 3
乙班参赛学生/人 1 2 3 4
分别求甲、乙两班参赛学生竞赛成绩的平均数和方差.
四、综合题
19.某学校组织七、八年级全体学生举行了安全知识竞赛活动,为了解竞赛成绩情况,为两个年级各随机抽取10名学生的成绩(满分为100分)进行了分析,并依据分析结果绘制了如下表所示的不完整统计表:
七年级:90,95,95,80,85,90,80,90,85,100;
八年级:85,85,95,80,95,90,90,90,100,90.
年级 平均数 中位数 众数 方差
七年级 89 m 90 39
八年级 n 90 p q
根据以上信息解答下面问题:
(1)填空:m= ,p= ;
(2)求q的值;
(3)通过数据分析,你认为哪个年级的成绩比较好?说明理由.
20.“防控疫情,全民力行”,某中学开展防疫知识线上竞赛活动,八年级(1),(2)班各选出5名选手参加竞赛,两个班选出的5名选手的竞赛成绩(满分为100分)如图所示.
(1)请你计算两个班的平均成绩各是多少分;
(2)已知八(2)班竞赛成绩的方差是114,请计算八(1)班竞赛成绩的方差,并说明哪个班的成绩较为整齐.
21.省篮球协会需要在某中学的优秀篮球运动员甲、乙两人中招收一名投篮较准且比较稳定的运动员,组织了7次定点投篮对抗赛,每次投篮10个,将两人的7次对抗赛中每次投进的个数统计如表.
甲 9 8 8 7 10 8 6
乙 10 9 8 9 4 8 8
(1)求甲、乙二人的中位数和众数分别是多少;
(2)应该招收哪位同学,并说明理由.
22.开展党史学习教育,是党中央因时因势作出的重大决策,是大力推进红色基因传承的重要举措,是凝聚智慧力量奋进新征程的现实需要.某学校在党员教师中开展了学习党史知识竞赛,将参赛的甲,乙两组党员教师成绩(单位:分)整理如下:
整理数据:
甲组:6,6,9,7,9,10,9.
乙组:7,6,10,5,9,9,10.
分析数据:
平均数 中位数 众数
甲组 8 b c
乙组 a 9 9和10
(1)表中的 , , ;
(2)已知甲组教师成绩的方差为,请计算乙组教师成绩的方差,并说明哪组教师的成绩更稳定?
23.2022年4月7日是第73个世界卫生日,某学校为纪念爱国卫生运动以及抗击新冠肺炎疫情决定在八年级举办卫生知识竞赛活动.甲,乙两班各选派5名学生参加学校卫生知识竞赛(满分100分).成绩如下(单位:分):
甲班:96,92,94,97,96;
乙班;90,98,97,98,92.
通过数据分析,列表如下:
班级 平均分 中位数 众数
甲班 a 96 96
乙班 95 b c
(1)填空:a= ,b= ,c= ;
(2)已知乙班学生竞赛成绩的方差为11.2,请计算甲班学生竞赛成绩的方差,并回答哪个班的学生竞赛成绩更稳定?
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】C
4.【答案】C
5.【答案】A
6.【答案】B
7.【答案】A
8.【答案】A
9.【答案】C
10.【答案】B
11.【答案】甲
12.【答案】乙
13.【答案】5;3
14.【答案】乙
15.【答案】乙
16.【答案】解: (分),
(分),
,
,
∵甲的方差大于乙的方差,
∴乙参加比赛比较合适.
17.【答案】解: (分)
∵
∴选择甲参加比赛较合适
18.【答案】解:甲班参赛学生的平均数是: (85×1+90×1+95×5+100×3)=95(分)
乙班参赛学生的平均数是: (85×1+90×2+95×3+100×4)=95(分)
则S甲2= [(85﹣95)2+(90﹣95)2+5(95﹣95)2+3(100﹣95)2]=20(分2)
S乙2= [(85﹣95)2+2(90﹣95)2+3(95﹣95)2+4(100﹣95)2]=25(分2)
答:甲、乙两班参赛学生竞赛成绩的平均数都是95分,方差分别为20分2,25分2.
19.【答案】(1)90|90
(2)解:八年级的平均数n=×(85×2+95×2+90×4+80+100)=90,方差为q=×[2×(85﹣90)2+2×(95﹣90)2+4×(90﹣90)2+(80﹣90)2+(100﹣90)2]=30;
(3)解:从平均分来看八年级高;通过方差来看,八年级的方差小,说明八年级的成绩稳定,所以八年级比较好.
20.【答案】(1)解:八(1)班的成绩分别为80,80,90,80,100;
八(2)班的成绩分别为80,100,95,70,85;
∴八(1)班的平均成绩为分;
八(2)班的平均成绩为分;
答:八(1)班平均成绩为86分,八(2)班平均成绩为86分.
(2)解:八(1)班竞赛成绩的方差为;
∵64<114,
∴八(1)班的成绩较为整齐.
21.【答案】(1)解:将甲的7个数据按照由小到大的顺序排列:6,7,8,8,8,9,10,
在最中间的数是8,8出现了3次,出现次数最多,
∴这组数据的中位数为8,众数为8.
将乙的7个数据按照由小到大的顺序排列:4,8,8,8,9,9,10,
在最中间的数是8,8出现了3次,出现次数最多,
∴这组数据的中位数为8,众数为8.
答:甲、乙二人的中位数和众数分别是8,8,8,8;
(2)解:应该招收甲同学.理由如下:
甲的平均数为.
甲的方差=×[(6-8)2+(7-8)2+3×(8-8)2+(9-8)2+(10-8)2]=,
乙的平均数为.
乙的方差=×[(4-8)2+3×(8-8)2+2×(9-8)2+(10-8)2]=,
∴甲、乙的平均成绩都为8,但甲的方差<乙的方差,
∴在平均数相同的情况下,甲的方差比乙小,故甲比乙稳定,应该招收甲同学.
22.【答案】(1)8;9;9
(2)解:.
,
甲组教师成绩的方差较小,成绩更为稳定.
23.【答案】(1)95;97;98
(2)解:由(1)知甲班同学竞赛成绩的平均分为95,
∴方差为: .
∵11.2>3.2,
∴甲班的学生竞赛成绩更稳定.
