2022-2023学年人教版八年级数学下册20.3 体质健康测试中的数据分析 课时训练(含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学下册20.3 体质健康测试中的数据分析 课时训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 352.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 08:19:15 | ||
图片预览



文档简介
20.3 体质健康测试中的数据分析 课时训练-2022-2023学年人教版八年级数学下册
一、单选题
1.据统计,无为市某月4日~10日的最高气温如下发所示,则下列说法错误的是( )
A.平均数是20 B.众数是20
C.5日~8日最高气温呈上升趋势 D.中位数是21
2.某校“啦啦操”兴趣小组共有50名学生,她们的年龄分布如下表:
年龄/岁 12 13 14 15
人数 5 23 ■ ■
由于表格污损,14岁、15岁人数看不清,则下列关于年龄的统计量可以确定的是( ).
A.平均数、众数 B.众数、中位数
C.平均数、中位数 D.中位数、方差
3.颠球是练习足球球感最基本的招式之一某校足球队10名球员在一次训练中的颠球测试成绩(以“次”为单位计)为:52,50,46,54,50,56,47,52,53,50.则以下数据中计算错误的是( )
A.平均数为51 B.方差为8.4 C.中位数为53 D.众数为50
4.下列表格反映了某公司员工的工资情况,该公司的应聘者最应该关注的数据是( )
职位 普工 文员 经理 董事长
人数 8 6 2 1
工资/元 2200 2600 4000 12000
A.平均数 B.众数与中位数
C.方差 D.最大数据
5.甲、乙、丙三名射击运动员在集训期间的测试成绩如下表所以,若需要在其中遴选一名成绩优异并稳定的运动员参加比赛,比较适合的运动员是( )
成绩/(环) 测试一 测试二 测试三 测试四 平均数 方差
甲 9.2 8.8 9.4 8.6 9.0 0.1
乙 8.8 8.6 8.7 9.1 8.8 0.035
丙 8.8 8.9 9.1 9.3 9.0 0.035
A.甲 B.乙 C.丙 D.无法确定
6.甲、乙两名学生在参加今年体育考试前各做了5次立定跳远测试,两人的平均成绩相同,其中甲所测得成绩的中位数是2.30m、方差是0.005,乙所测得成绩的中位数是2.35m、方差是0.016,那么成绩较为稳定的同学是( )
A.乙同学 B.甲、乙两人一样
C.甲同学 D.无法确定
7.为了解新冠肺炎疫情防控期间,学生居家进行“线上学习”情况,某班进行了某学科单元基础知识“线上测试”,其中抽查的名学生的成绩如图所示,对于这名学生的测试成绩,下列说法正确的有( )
①中位数是分;②众数是分;③平均数是分;④方差是
A. B. C. D.
8.某组数据方差计算公式为:,由公式提供的信息,下列说法错误的是( )
A.样本的容量是3 B.样本的中位数是3
C.样本的众数是3 D.样本的平均数是3
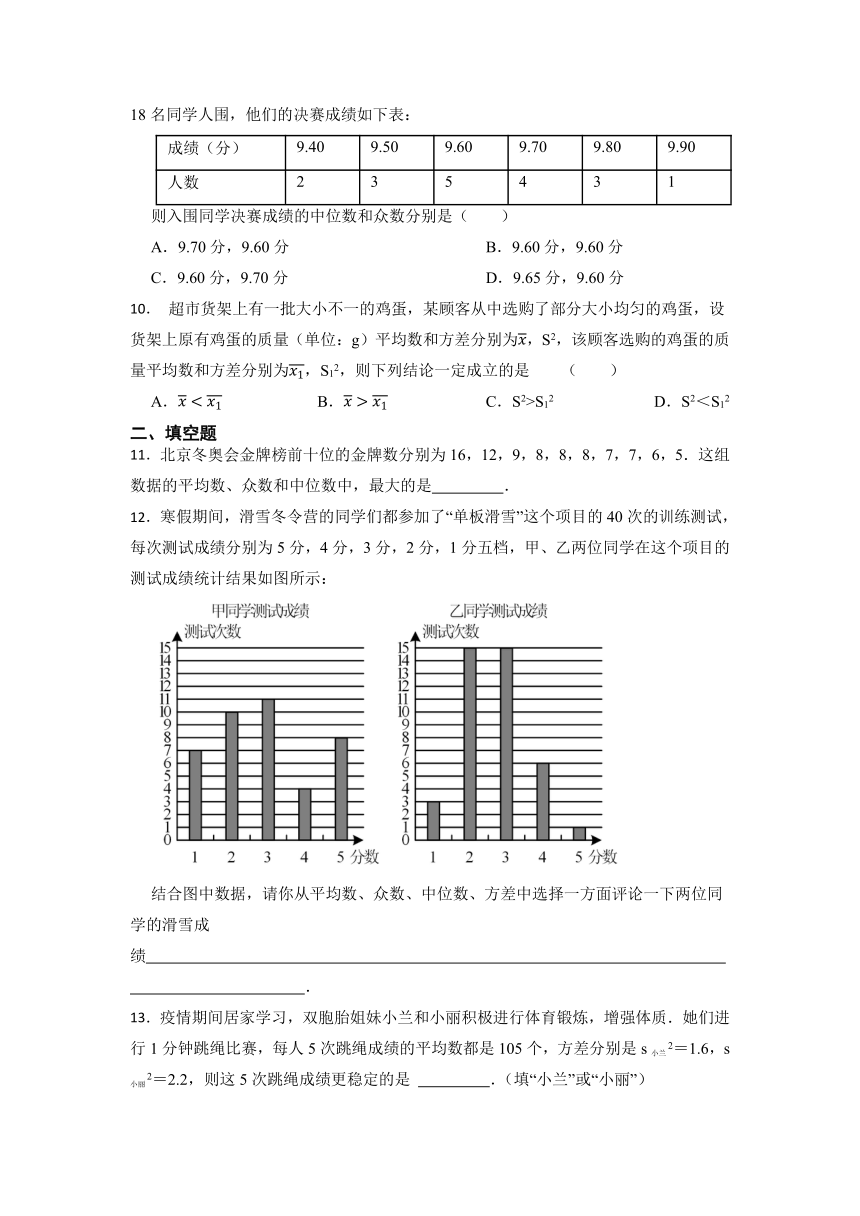
9.学校为了丰富学生课余活动,开展了一次“爱我中华,唱我中华”的歌咏比赛,共有18名同学人围,他们的决赛成绩如下表:
成绩(分) 9.40 9.50 9.60 9.70 9.80 9.90
人数 2 3 5 4 3 1
则入围同学决赛成绩的中位数和众数分别是( )
A.9.70分,9.60分 B.9.60分,9.60分
C.9.60分,9.70分 D.9.65分,9.60分
10. 超市货架上有一批大小不一的鸡蛋,某顾客从中选购了部分大小均匀的鸡蛋,设货架上原有鸡蛋的质量(单位:g)平均数和方差分别为,S2,该顾客选购的鸡蛋的质量平均数和方差分别为,S12,则下列结论一定成立的是 ( )
A. B. C.S2>S12 D.S2<S12
二、填空题
11.北京冬奥会金牌榜前十位的金牌数分别为16,12,9,8,8,8,7,7,6,5.这组数据的平均数、众数和中位数中,最大的是 .
12.寒假期间,滑雪冬令营的同学们都参加了“单板滑雪”这个项目的40次的训练测试,每次测试成绩分别为5分,4分,3分,2分,1分五档,甲、乙两位同学在这个项目的测试成绩统计结果如图所示:
结合图中数据,请你从平均数、众数、中位数、方差中选择一方面评论一下两位同学的滑雪成绩 .
13.疫情期间居家学习,双胞胎姐妹小兰和小丽积极进行体育锻炼,增强体质.她们进行1分钟跳绳比赛,每人5次跳绳成绩的平均数都是105个,方差分别是s小兰2=1.6,s小丽2=2.2,则这5次跳绳成绩更稳定的是 .(填“小兰”或“小丽”)
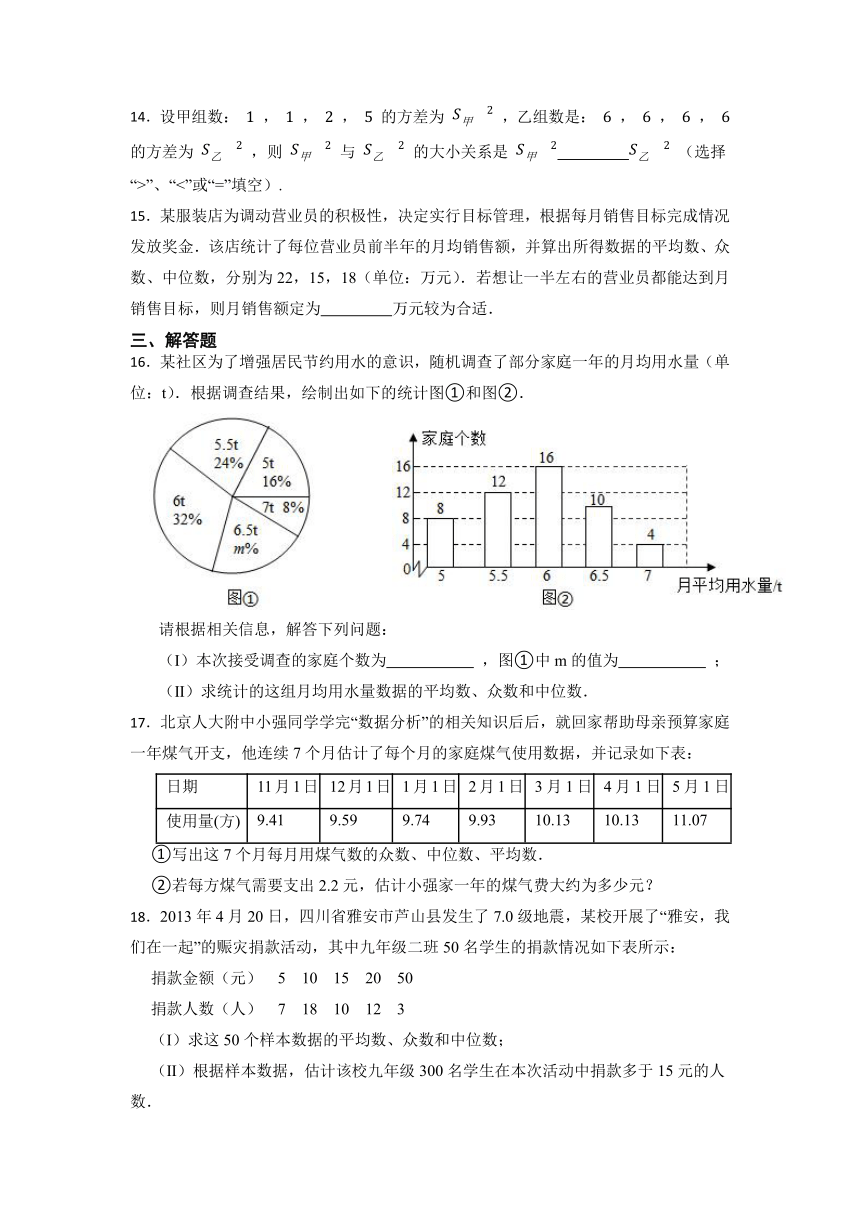
14.设甲组数: , , , 的方差为 ,乙组数是: , , , 的方差为 ,则 与 的大小关系是 (选择“>”、“<”或“=”填空).
15.某服装店为调动营业员的积极性,决定实行目标管理,根据每月销售目标完成情况发放奖金.该店统计了每位营业员前半年的月均销售额,并算出所得数据的平均数、众数、中位数,分别为22,15,18(单位:万元).若想让一半左右的营业员都能达到月销售目标,则月销售额定为 万元较为合适.
三、解答题
16.某社区为了增强居民节约用水的意识,随机调查了部分家庭一年的月均用水量(单位:t).根据调查结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的家庭个数为 ,图①中m的值为 ;
(Ⅱ)求统计的这组月均用水量数据的平均数、众数和中位数.
17.北京人大附中小强同学学完“数据分析”的相关知识后后,就回家帮助母亲预算家庭一年煤气开支,他连续7个月估计了每个月的家庭煤气使用数据,并记录如下表:
日期 11月1日 12月1日 1月1日 2月1日 3月1日 4月1日 5月1日
使用量(方) 9.41 9.59 9.74 9.93 10.13 10.13 11.07
①写出这7个月每月用煤气数的众数、中位数、平均数.
②若每方煤气需要支出2.2元,估计小强家一年的煤气费大约为多少元?
18.2013年4月20日,四川省雅安市芦山县发生了7.0级地震,某校开展了“雅安,我们在一起”的赈灾捐款活动,其中九年级二班50名学生的捐款情况如下表所示:
捐款金额(元) 5 10 15 20 50
捐款人数(人) 7 18 10 12 3
(Ⅰ)求这50个样本数据的平均数、众数和中位数;
(Ⅱ)根据样本数据,估计该校九年级300名学生在本次活动中捐款多于15元的人数.
四、综合题
19.甲乙两名射击运动员10次射击训练成绩如下表(10环制):
甲 7 10 9 7 8 10 9 10 10 10
乙 7 8 10 9 8 10 10 9 10 9
(1)填空:甲运动员成绩的众数是 环,乙运动员成绩的中位数是 环;
(2)计算甲运动员的平均成绩和方差.
20.2022年6月5日,神舟十四号载人飞船计划成功发射,激发了同学们的爱国热情.某校为了解七、八年级学生对“航空航天”知识的掌握情况,对七、八年级学生进行了测试,现从七、八年级各随机抽取了15名学生的测试成绩进行了以下数据的整理与分析:
数据收集:
七年级:82,83,78,89,96,98,84,65,73,72,85,70,85,92,93
八年级:93,77,88,85,73,88,90,79,94,88,69,56,93,90,82
数据整理:
分数段
七年级 1 4 a 4
八年级 2 3 5 5
数据分析:
年级 平均数 中位数 众数
七年级 83 b 85
八年级 83 88 c
根据以上信息,解答下列问题:
(1) , , ;
(2)请推断哪个年级的测试成绩较好,并说明理由(写出一条理由即可);
(3)测试成绩在分的学生可以获得奖励,若该校七年级有600名学生,八年级有660名学生,估计七、八年级可以获得奖励的学生总人数为多少.
21.某乡镇企业生产部有技术工人15人,生产部为了合理计划产品的月生产定额,统计这15人某月加工零件个数如下:
加工零件个数(个) 540 450 300 240 210 120
人数(人) 1 1 2 6 3 2
(1)写出15人该月加工零件个数的平均数、中位数和众数;
(2)假设生产部负责人把每位工人的月加工零件个数定为260,你认为是否合理?为什么?若不合理,请你设定一个较为合理的定额,并说明理由.
22.甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环 中位数/环 众数/环 方差
甲
乙
(1)写出表格中 的值:
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名
参赛,你认为应选哪名队员?说明你的理由。
23.2022年,疫情依然还没有离我们而去,全民抗疫,需要您我他.某校为了了解七年级共480名同学对防疫知识的掌握情况,对他们进行了防疫知识测试,现随机抽取甲、乙两班各15名同学的测试成绩进行整理分析,过程如下:
【收集数据】
甲班15名学生测试成绩分别为:
78,83,89,97,98,85,100,94,87,90,93,92,99,95,100
乙班15名学生测试成绩中的成绩如下:91,92,94,90,93
【整理数据】
班级
甲 1 1 3 6
乙 1 2 3 5 4
【分析数据】
班级 平均数 众数 中位数 方差
甲 92 93 41.7
乙 90 87 50.2
【应用数据】
(1)根据以上信息,可以求出: , 分, 分;
(2)根据以上数据,你认为哪个班的学生防疫测试的整体成绩较好?并至少从两个方面说明理由.
答案解析部分
1.【答案】A
2.【答案】B
3.【答案】C
4.【答案】B
5.【答案】C
6.【答案】C
7.【答案】B
8.【答案】A
9.【答案】B
10.【答案】C
11.【答案】平均数
12.【答案】从平均数看甲同学成绩好(或从中位数看两个同学的成绩一样或从方差看乙的成绩稳定).答案不唯一
13.【答案】小兰
14.【答案】
15.【答案】18
16.【答案】解:(Ⅰ)50,20;
(Ⅱ)平均数:吨,
∵用水量6吨的家庭个数为16,最多,
∴众数=6吨,
∵一共50个数据,最中间的数据为第25和第26个数据,
∴中位数=(6+6)÷2=6吨.
答: 这组月均用水量数据的平均数为5.9吨,众数为6吨,中位数为6吨.
17.【答案】解:①10.13出现了2次,最多,所以众数为10.13;排序后位于中间位置的数是9.93,所以中位数为9.93,
平均数为: .
②小强家一年的煤气费为10×12×2.2=264元
18.【答案】解:(Ⅰ)观察表格,可知这组样本数据的平均数是 = =15.1;
∴这组样本数据的平均数是15.1
在这组样本数据中,10出现了18次,出现的次数最多,
∴这组样本数据的众数为10
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数分别是10,15,
∴这组数据的中位数为l2.5
(Ⅱ)在50名学生中,捐款多于15元的学生有15名,有300× =90(名).
∴根据样本数据,可以估计该校九年级300名学生在本次活动中捐款多于15元的约有90名.
19.【答案】(1)10;9
(2)解:,
或,
.
20.【答案】(1)6;84;86
(2)解:由于七、八年级成绩平均数相同,而八年级的中位数、众数均高于七年级,因此八年级的成绩较好.
(3)解:
故七、八年级可以获得奖励的学生总人数为380人.
21.【答案】(1)解:平均数,
将表中的数据按照从小到大的顺序排列,可得出第8名工人的加工零件数为240件,且零件加工数为240件的工人最多,
故中位数为:240,众数为:240.
因此这15人该月加工零件数的平均数为260,中位数为240,众数为240.
(2)解:不合理,理由是:260超过了中位数240,只有4个人可以达到定额,大部分人都达不到定额;
240较为合理,理由是:240既是众数,也是中位数,且240小于人均零件加工数,是大多数人能达到的定额.
22.【答案】(1)解:甲的平均成绩 (环),
∵乙射击的成绩从小到大从新排列为:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数 (环),
又∵乙射击的成绩从小到大从新排列为:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的众数:c=8(环)
其方差为:
= ×(16+9+1+0+3+4+9)= = ;
(2)解:从平均成绩看甲、乙二人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看甲的成绩比乙的成绩稳定, 综合以上各因素,若选派一名学生参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大.
23.【答案】(1)4;100;91
(2)解:甲班的学生防疫测试的整体成绩较好
从平均数看,甲的平均数大于乙的平均数;
从方差看,甲的方差小于乙的方差,故甲比较稳定;
从中位数的角度看,甲的中位数大于乙的中位数,甲的整体成绩比乙的整体成绩好.
一、单选题
1.据统计,无为市某月4日~10日的最高气温如下发所示,则下列说法错误的是( )
A.平均数是20 B.众数是20
C.5日~8日最高气温呈上升趋势 D.中位数是21
2.某校“啦啦操”兴趣小组共有50名学生,她们的年龄分布如下表:
年龄/岁 12 13 14 15
人数 5 23 ■ ■
由于表格污损,14岁、15岁人数看不清,则下列关于年龄的统计量可以确定的是( ).
A.平均数、众数 B.众数、中位数
C.平均数、中位数 D.中位数、方差
3.颠球是练习足球球感最基本的招式之一某校足球队10名球员在一次训练中的颠球测试成绩(以“次”为单位计)为:52,50,46,54,50,56,47,52,53,50.则以下数据中计算错误的是( )
A.平均数为51 B.方差为8.4 C.中位数为53 D.众数为50
4.下列表格反映了某公司员工的工资情况,该公司的应聘者最应该关注的数据是( )
职位 普工 文员 经理 董事长
人数 8 6 2 1
工资/元 2200 2600 4000 12000
A.平均数 B.众数与中位数
C.方差 D.最大数据
5.甲、乙、丙三名射击运动员在集训期间的测试成绩如下表所以,若需要在其中遴选一名成绩优异并稳定的运动员参加比赛,比较适合的运动员是( )
成绩/(环) 测试一 测试二 测试三 测试四 平均数 方差
甲 9.2 8.8 9.4 8.6 9.0 0.1
乙 8.8 8.6 8.7 9.1 8.8 0.035
丙 8.8 8.9 9.1 9.3 9.0 0.035
A.甲 B.乙 C.丙 D.无法确定
6.甲、乙两名学生在参加今年体育考试前各做了5次立定跳远测试,两人的平均成绩相同,其中甲所测得成绩的中位数是2.30m、方差是0.005,乙所测得成绩的中位数是2.35m、方差是0.016,那么成绩较为稳定的同学是( )
A.乙同学 B.甲、乙两人一样
C.甲同学 D.无法确定
7.为了解新冠肺炎疫情防控期间,学生居家进行“线上学习”情况,某班进行了某学科单元基础知识“线上测试”,其中抽查的名学生的成绩如图所示,对于这名学生的测试成绩,下列说法正确的有( )
①中位数是分;②众数是分;③平均数是分;④方差是
A. B. C. D.
8.某组数据方差计算公式为:,由公式提供的信息,下列说法错误的是( )
A.样本的容量是3 B.样本的中位数是3
C.样本的众数是3 D.样本的平均数是3
9.学校为了丰富学生课余活动,开展了一次“爱我中华,唱我中华”的歌咏比赛,共有18名同学人围,他们的决赛成绩如下表:
成绩(分) 9.40 9.50 9.60 9.70 9.80 9.90
人数 2 3 5 4 3 1
则入围同学决赛成绩的中位数和众数分别是( )
A.9.70分,9.60分 B.9.60分,9.60分
C.9.60分,9.70分 D.9.65分,9.60分
10. 超市货架上有一批大小不一的鸡蛋,某顾客从中选购了部分大小均匀的鸡蛋,设货架上原有鸡蛋的质量(单位:g)平均数和方差分别为,S2,该顾客选购的鸡蛋的质量平均数和方差分别为,S12,则下列结论一定成立的是 ( )
A. B. C.S2>S12 D.S2<S12
二、填空题
11.北京冬奥会金牌榜前十位的金牌数分别为16,12,9,8,8,8,7,7,6,5.这组数据的平均数、众数和中位数中,最大的是 .
12.寒假期间,滑雪冬令营的同学们都参加了“单板滑雪”这个项目的40次的训练测试,每次测试成绩分别为5分,4分,3分,2分,1分五档,甲、乙两位同学在这个项目的测试成绩统计结果如图所示:
结合图中数据,请你从平均数、众数、中位数、方差中选择一方面评论一下两位同学的滑雪成绩 .
13.疫情期间居家学习,双胞胎姐妹小兰和小丽积极进行体育锻炼,增强体质.她们进行1分钟跳绳比赛,每人5次跳绳成绩的平均数都是105个,方差分别是s小兰2=1.6,s小丽2=2.2,则这5次跳绳成绩更稳定的是 .(填“小兰”或“小丽”)
14.设甲组数: , , , 的方差为 ,乙组数是: , , , 的方差为 ,则 与 的大小关系是 (选择“>”、“<”或“=”填空).
15.某服装店为调动营业员的积极性,决定实行目标管理,根据每月销售目标完成情况发放奖金.该店统计了每位营业员前半年的月均销售额,并算出所得数据的平均数、众数、中位数,分别为22,15,18(单位:万元).若想让一半左右的营业员都能达到月销售目标,则月销售额定为 万元较为合适.
三、解答题
16.某社区为了增强居民节约用水的意识,随机调查了部分家庭一年的月均用水量(单位:t).根据调查结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的家庭个数为 ,图①中m的值为 ;
(Ⅱ)求统计的这组月均用水量数据的平均数、众数和中位数.
17.北京人大附中小强同学学完“数据分析”的相关知识后后,就回家帮助母亲预算家庭一年煤气开支,他连续7个月估计了每个月的家庭煤气使用数据,并记录如下表:
日期 11月1日 12月1日 1月1日 2月1日 3月1日 4月1日 5月1日
使用量(方) 9.41 9.59 9.74 9.93 10.13 10.13 11.07
①写出这7个月每月用煤气数的众数、中位数、平均数.
②若每方煤气需要支出2.2元,估计小强家一年的煤气费大约为多少元?
18.2013年4月20日,四川省雅安市芦山县发生了7.0级地震,某校开展了“雅安,我们在一起”的赈灾捐款活动,其中九年级二班50名学生的捐款情况如下表所示:
捐款金额(元) 5 10 15 20 50
捐款人数(人) 7 18 10 12 3
(Ⅰ)求这50个样本数据的平均数、众数和中位数;
(Ⅱ)根据样本数据,估计该校九年级300名学生在本次活动中捐款多于15元的人数.
四、综合题
19.甲乙两名射击运动员10次射击训练成绩如下表(10环制):
甲 7 10 9 7 8 10 9 10 10 10
乙 7 8 10 9 8 10 10 9 10 9
(1)填空:甲运动员成绩的众数是 环,乙运动员成绩的中位数是 环;
(2)计算甲运动员的平均成绩和方差.
20.2022年6月5日,神舟十四号载人飞船计划成功发射,激发了同学们的爱国热情.某校为了解七、八年级学生对“航空航天”知识的掌握情况,对七、八年级学生进行了测试,现从七、八年级各随机抽取了15名学生的测试成绩进行了以下数据的整理与分析:
数据收集:
七年级:82,83,78,89,96,98,84,65,73,72,85,70,85,92,93
八年级:93,77,88,85,73,88,90,79,94,88,69,56,93,90,82
数据整理:
分数段
七年级 1 4 a 4
八年级 2 3 5 5
数据分析:
年级 平均数 中位数 众数
七年级 83 b 85
八年级 83 88 c
根据以上信息,解答下列问题:
(1) , , ;
(2)请推断哪个年级的测试成绩较好,并说明理由(写出一条理由即可);
(3)测试成绩在分的学生可以获得奖励,若该校七年级有600名学生,八年级有660名学生,估计七、八年级可以获得奖励的学生总人数为多少.
21.某乡镇企业生产部有技术工人15人,生产部为了合理计划产品的月生产定额,统计这15人某月加工零件个数如下:
加工零件个数(个) 540 450 300 240 210 120
人数(人) 1 1 2 6 3 2
(1)写出15人该月加工零件个数的平均数、中位数和众数;
(2)假设生产部负责人把每位工人的月加工零件个数定为260,你认为是否合理?为什么?若不合理,请你设定一个较为合理的定额,并说明理由.
22.甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环 中位数/环 众数/环 方差
甲
乙
(1)写出表格中 的值:
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名
参赛,你认为应选哪名队员?说明你的理由。
23.2022年,疫情依然还没有离我们而去,全民抗疫,需要您我他.某校为了了解七年级共480名同学对防疫知识的掌握情况,对他们进行了防疫知识测试,现随机抽取甲、乙两班各15名同学的测试成绩进行整理分析,过程如下:
【收集数据】
甲班15名学生测试成绩分别为:
78,83,89,97,98,85,100,94,87,90,93,92,99,95,100
乙班15名学生测试成绩中的成绩如下:91,92,94,90,93
【整理数据】
班级
甲 1 1 3 6
乙 1 2 3 5 4
【分析数据】
班级 平均数 众数 中位数 方差
甲 92 93 41.7
乙 90 87 50.2
【应用数据】
(1)根据以上信息,可以求出: , 分, 分;
(2)根据以上数据,你认为哪个班的学生防疫测试的整体成绩较好?并至少从两个方面说明理由.
答案解析部分
1.【答案】A
2.【答案】B
3.【答案】C
4.【答案】B
5.【答案】C
6.【答案】C
7.【答案】B
8.【答案】A
9.【答案】B
10.【答案】C
11.【答案】平均数
12.【答案】从平均数看甲同学成绩好(或从中位数看两个同学的成绩一样或从方差看乙的成绩稳定).答案不唯一
13.【答案】小兰
14.【答案】
15.【答案】18
16.【答案】解:(Ⅰ)50,20;
(Ⅱ)平均数:吨,
∵用水量6吨的家庭个数为16,最多,
∴众数=6吨,
∵一共50个数据,最中间的数据为第25和第26个数据,
∴中位数=(6+6)÷2=6吨.
答: 这组月均用水量数据的平均数为5.9吨,众数为6吨,中位数为6吨.
17.【答案】解:①10.13出现了2次,最多,所以众数为10.13;排序后位于中间位置的数是9.93,所以中位数为9.93,
平均数为: .
②小强家一年的煤气费为10×12×2.2=264元
18.【答案】解:(Ⅰ)观察表格,可知这组样本数据的平均数是 = =15.1;
∴这组样本数据的平均数是15.1
在这组样本数据中,10出现了18次,出现的次数最多,
∴这组样本数据的众数为10
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数分别是10,15,
∴这组数据的中位数为l2.5
(Ⅱ)在50名学生中,捐款多于15元的学生有15名,有300× =90(名).
∴根据样本数据,可以估计该校九年级300名学生在本次活动中捐款多于15元的约有90名.
19.【答案】(1)10;9
(2)解:,
或,
.
20.【答案】(1)6;84;86
(2)解:由于七、八年级成绩平均数相同,而八年级的中位数、众数均高于七年级,因此八年级的成绩较好.
(3)解:
故七、八年级可以获得奖励的学生总人数为380人.
21.【答案】(1)解:平均数,
将表中的数据按照从小到大的顺序排列,可得出第8名工人的加工零件数为240件,且零件加工数为240件的工人最多,
故中位数为:240,众数为:240.
因此这15人该月加工零件数的平均数为260,中位数为240,众数为240.
(2)解:不合理,理由是:260超过了中位数240,只有4个人可以达到定额,大部分人都达不到定额;
240较为合理,理由是:240既是众数,也是中位数,且240小于人均零件加工数,是大多数人能达到的定额.
22.【答案】(1)解:甲的平均成绩 (环),
∵乙射击的成绩从小到大从新排列为:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数 (环),
又∵乙射击的成绩从小到大从新排列为:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的众数:c=8(环)
其方差为:
= ×(16+9+1+0+3+4+9)= = ;
(2)解:从平均成绩看甲、乙二人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看甲的成绩比乙的成绩稳定, 综合以上各因素,若选派一名学生参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大.
23.【答案】(1)4;100;91
(2)解:甲班的学生防疫测试的整体成绩较好
从平均数看,甲的平均数大于乙的平均数;
从方差看,甲的方差小于乙的方差,故甲比较稳定;
从中位数的角度看,甲的中位数大于乙的中位数,甲的整体成绩比乙的整体成绩好.
