2022-2023学年人教版数学七年级下册 5.1.2 垂线同步训练必刷题 (无答案)
文档属性
| 名称 | 2022-2023学年人教版数学七年级下册 5.1.2 垂线同步训练必刷题 (无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 341.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 08:21:53 | ||
图片预览

文档简介
5.1.2 垂线同步训练必刷题-2022-2023学年人教版初中数学七年级下册
一、单选题(每题3分,共30分)
1.点P为直线l外一点,点A、B、C为直线l上三点,PA=4cm,PB=5cm,PC=3cm,则点P到直线l的距离为( )
A.4cm B.5cm C.小于3cm D.不大于3cm
2.下列图形中,线段的长表示点A到直线的距离的是( )
A. B.
C. D.
3.如图,河道的同侧有、两地,现要铺设一条引水管道,从地把河水引向、两地.下列四种方案中,最节省材料的是( )
A. B.
C. D.
4.已知三条射线OA,OB,OC,OA⊥OC,∠AOB=60°,则∠BOC等于( )
A.150° B.30° C.40°或140° D.30°或150°
5.如图,在测量跳远成绩的示意图中,直线是起跳线,则需要测量的线段是( )
A. B. C. D.
6.如图,在中,,,垂足为点D,那么点A到直线的距离是线段()的长.
A. B. C. D.
7.如图,点O在直线CD上,OB⊥OA.若∠BOD=110°,则∠AOC的度数为()
A.10° B.20° C.60° D.70°
8.如图所示,点C到AB所在的直线的距离是指图中线段( )的长度.
A.AE B.CF C.BD D.BE
9.如图,某同学在体育课上跳远后留下的脚印,在图中画出了他的跳远距离,能正确解释这一现象的数学知识是( )
A.两点之间,线段最短
B.垂线段最短
C.两点确定一条直线
D.经过一点有且只有一条直线与已知直线垂直
10.小明在做一道数学题.直线AB,CD相交于点O,∠BOC=25°,过点O作 ,求∠AOE的度数.小明得到 ,但老师说他少了一个答案.那么∠AOE的另一个值是( )
A.105° B.115° C.125° D.135°
二、填空题(每题3分,共30分)
11.如图,点P是直线l外一点,过点P作于点O,点A是直线l上任意一点,连接,若,则的长可能是 (写出一个即可).
12.如图,农民伯伯若要将河里的水引到田地P处,需要从点P作河岸l的垂线,垂足是Q,则沿PQ挖的水沟最短,这样做的数学道理是 .
13.已知直线AB与直线CD相交于点O,∠AOC:∠BOC=2:1,射线OE⊥CD,则∠AOE的度数为 .
14.如图,在三角形中,,,,,则点A到的距离等于 .
15.如图直线AB、CD、EF相交于点O,且AB⊥CD,∠1=40°,则∠2= .
16.如图,为了方便人们从A点到道路l上,学校过A点作直线l垂线,垂足为B点,这样做的数学原理是 .
17.如图,直线相交于O,平分,若,则的度数为 .
18.如图所示,要在河堤两岸搭建一座桥,搭建方式中最短的是线段 ,理由是 .
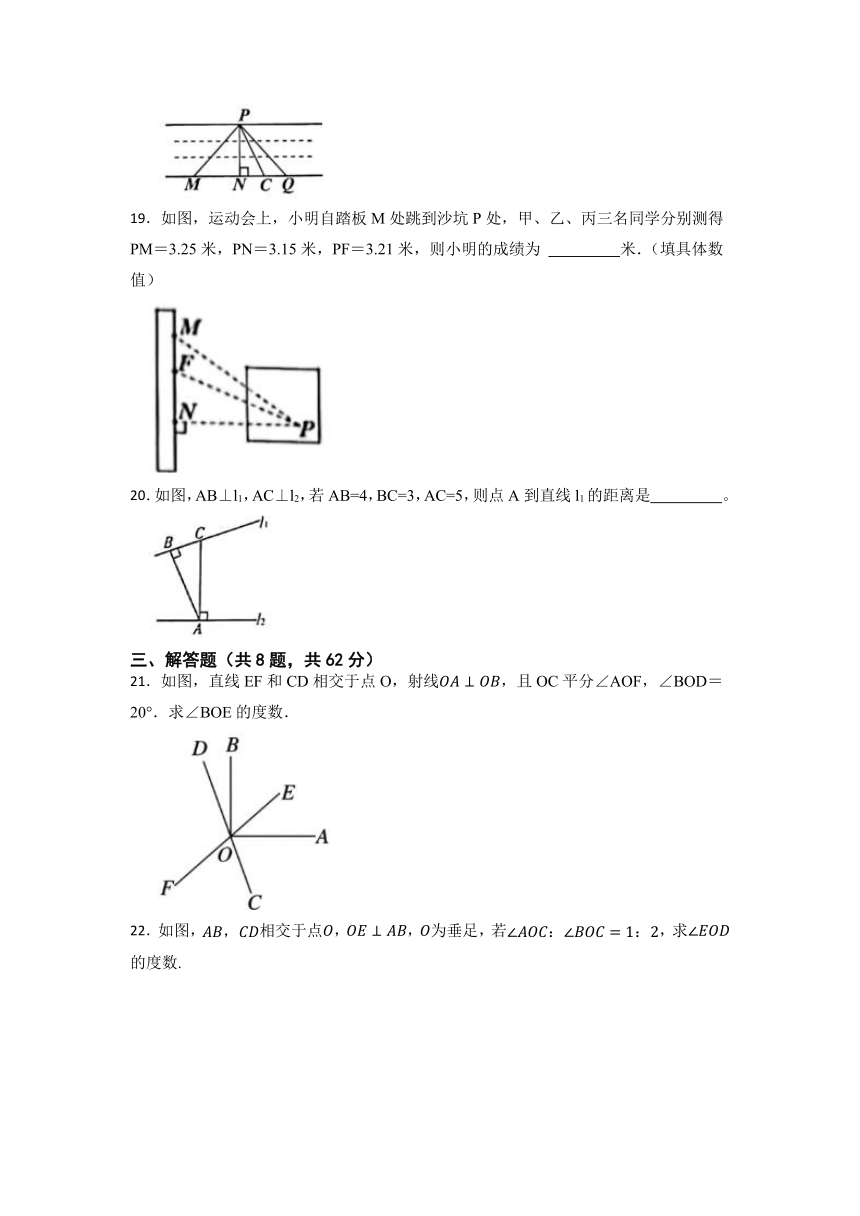
19.如图,运动会上,小明自踏板M处跳到沙坑P处,甲、乙、丙三名同学分别测得PM=3.25米,PN=3.15米,PF=3.21米,则小明的成绩为 米.(填具体数值)
20.如图,AB⊥l1,AC⊥l2,若AB=4,BC=3,AC=5,则点A到直线l1的距离是 。
三、解答题(共8题,共62分)
21.如图,直线EF和CD相交于点O,射线,且OC平分∠AOF,∠BOD=20°.求∠BOE的度数.
22.如图,相交于点,,为垂足,若,求的度数.
23.如图,直线,相交于点,,若,,求的度数.
24.如图,直线AB,CD相交于点O,OE⊥CD于点O,∠EOB=115°,求∠AOC的度数.请补全下面的解题过程(括号中填写推理的依据).
解:∵OE⊥CD于点O(已知),
∴_▲_( ).
∵∠EOB=115°(已知),
∴∠DOB=_▲__=115°-90°=25°.
∵直线AB,CD相交于点O(已知),
∴∠AOC=_▲_=25°( ).
25.如图,已知线段,用三角板或量角器分别过P、D、F三点作线段的垂线.
26.如图,点在直线外,点在直线上,连接.选择适当的工具作图.
(1)在直线上作点,使,连接;
(2)在的延长线上任取一点,连接;
(3)在,,中,最短的线段是 ,依据是 .
27.如图,直线相交于点O,于点O.
(1)若,求的度数.
(2)若,请判断与关系,并说明理由.
28.如图,点O在直线AB上,OC平分,.
(1)已知,求的大小;
(2)若,请判断OE是否平分,并说明理由.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】D
4.【答案】D
5.【答案】C
6.【答案】D
7.【答案】B
8.【答案】B
9.【答案】B
10.【答案】B
11.【答案】4
12.【答案】垂线段最短
13.【答案】30°或150°
14.【答案】3
15.【答案】50°或50度
16.【答案】垂线段最短
17.【答案】67
18.【答案】垂线段最短
19.【答案】3.15
20.【答案】4
21.【答案】解:∵,
∴,
又∵,
∴,
∵OC平分∠AOF,
∴,
∴,
∴.
22.【答案】解:设∠AOC=x,则∠BOC=2x,
∵∠AOC+∠BOC=180°,
∴x+2x=180°,
解得:x=60°,
∴∠AOC=60°,
∴∠BOD=60°,
∵OE⊥AB,
∴∠EOB=90°,
∴∠EOD=∠EOB-∠BOD=90°-60°=30°.
23.【答案】解:
24.【答案】解:∵OE⊥CD于点O(已知),
∴∠EOD=90°(垂直的定义),
∵∠EOB=115°(已知),
∴∠DOB=∠EOB-∠EOD=115°-90°=25°.
∵直线AB,CD相交于点O(已知),
∴∠AOC=∠DOB=25°(对顶角相等).
故答案为:∠EOD=90°;垂直的定义;∠EOB-∠EOD;∠DOB;对顶角相等.
25.【答案】解:用三角板直接过点P、D作线段的垂线,延长AB,用三角板直接过点F作线段延长线的垂线,则直线l、直线m、直线n即为所求,如图所示:
26.【答案】(1)解:利用直角三角板和直尺作图如下:
(2)解:利用直尺连接,作图如下:
(3);垂线段最短
27.【答案】(1)解:由邻补角的定义,得∠AOC+∠BOC=180°,
∵∠BOC=4∠AOC,
∴4∠AOC+∠AOC=180°,
∴∠AOC=36°,
由对顶角相等,得
∠BOD=∠AOC=36°;
(2)解:ON⊥CD,理由如下:
∵OM⊥AB,
∴∠AOM=90°,
∴∠1+∠AOC=90°,
∵∠1=∠2,
∴∠2+∠AOC=90°,
即∠NOC=90°,
∴ON⊥CD.
28.【答案】(1)解:OC平分,,
,
,
,
又,
;
(2)解:OE平分,理由如下:
平分,,
,
又,
;
平分.
一、单选题(每题3分,共30分)
1.点P为直线l外一点,点A、B、C为直线l上三点,PA=4cm,PB=5cm,PC=3cm,则点P到直线l的距离为( )
A.4cm B.5cm C.小于3cm D.不大于3cm
2.下列图形中,线段的长表示点A到直线的距离的是( )
A. B.
C. D.
3.如图,河道的同侧有、两地,现要铺设一条引水管道,从地把河水引向、两地.下列四种方案中,最节省材料的是( )
A. B.
C. D.
4.已知三条射线OA,OB,OC,OA⊥OC,∠AOB=60°,则∠BOC等于( )
A.150° B.30° C.40°或140° D.30°或150°
5.如图,在测量跳远成绩的示意图中,直线是起跳线,则需要测量的线段是( )
A. B. C. D.
6.如图,在中,,,垂足为点D,那么点A到直线的距离是线段()的长.
A. B. C. D.
7.如图,点O在直线CD上,OB⊥OA.若∠BOD=110°,则∠AOC的度数为()
A.10° B.20° C.60° D.70°
8.如图所示,点C到AB所在的直线的距离是指图中线段( )的长度.
A.AE B.CF C.BD D.BE
9.如图,某同学在体育课上跳远后留下的脚印,在图中画出了他的跳远距离,能正确解释这一现象的数学知识是( )
A.两点之间,线段最短
B.垂线段最短
C.两点确定一条直线
D.经过一点有且只有一条直线与已知直线垂直
10.小明在做一道数学题.直线AB,CD相交于点O,∠BOC=25°,过点O作 ,求∠AOE的度数.小明得到 ,但老师说他少了一个答案.那么∠AOE的另一个值是( )
A.105° B.115° C.125° D.135°
二、填空题(每题3分,共30分)
11.如图,点P是直线l外一点,过点P作于点O,点A是直线l上任意一点,连接,若,则的长可能是 (写出一个即可).
12.如图,农民伯伯若要将河里的水引到田地P处,需要从点P作河岸l的垂线,垂足是Q,则沿PQ挖的水沟最短,这样做的数学道理是 .
13.已知直线AB与直线CD相交于点O,∠AOC:∠BOC=2:1,射线OE⊥CD,则∠AOE的度数为 .
14.如图,在三角形中,,,,,则点A到的距离等于 .
15.如图直线AB、CD、EF相交于点O,且AB⊥CD,∠1=40°,则∠2= .
16.如图,为了方便人们从A点到道路l上,学校过A点作直线l垂线,垂足为B点,这样做的数学原理是 .
17.如图,直线相交于O,平分,若,则的度数为 .
18.如图所示,要在河堤两岸搭建一座桥,搭建方式中最短的是线段 ,理由是 .
19.如图,运动会上,小明自踏板M处跳到沙坑P处,甲、乙、丙三名同学分别测得PM=3.25米,PN=3.15米,PF=3.21米,则小明的成绩为 米.(填具体数值)
20.如图,AB⊥l1,AC⊥l2,若AB=4,BC=3,AC=5,则点A到直线l1的距离是 。
三、解答题(共8题,共62分)
21.如图,直线EF和CD相交于点O,射线,且OC平分∠AOF,∠BOD=20°.求∠BOE的度数.
22.如图,相交于点,,为垂足,若,求的度数.
23.如图,直线,相交于点,,若,,求的度数.
24.如图,直线AB,CD相交于点O,OE⊥CD于点O,∠EOB=115°,求∠AOC的度数.请补全下面的解题过程(括号中填写推理的依据).
解:∵OE⊥CD于点O(已知),
∴_▲_( ).
∵∠EOB=115°(已知),
∴∠DOB=_▲__=115°-90°=25°.
∵直线AB,CD相交于点O(已知),
∴∠AOC=_▲_=25°( ).
25.如图,已知线段,用三角板或量角器分别过P、D、F三点作线段的垂线.
26.如图,点在直线外,点在直线上,连接.选择适当的工具作图.
(1)在直线上作点,使,连接;
(2)在的延长线上任取一点,连接;
(3)在,,中,最短的线段是 ,依据是 .
27.如图,直线相交于点O,于点O.
(1)若,求的度数.
(2)若,请判断与关系,并说明理由.
28.如图,点O在直线AB上,OC平分,.
(1)已知,求的大小;
(2)若,请判断OE是否平分,并说明理由.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】D
4.【答案】D
5.【答案】C
6.【答案】D
7.【答案】B
8.【答案】B
9.【答案】B
10.【答案】B
11.【答案】4
12.【答案】垂线段最短
13.【答案】30°或150°
14.【答案】3
15.【答案】50°或50度
16.【答案】垂线段最短
17.【答案】67
18.【答案】垂线段最短
19.【答案】3.15
20.【答案】4
21.【答案】解:∵,
∴,
又∵,
∴,
∵OC平分∠AOF,
∴,
∴,
∴.
22.【答案】解:设∠AOC=x,则∠BOC=2x,
∵∠AOC+∠BOC=180°,
∴x+2x=180°,
解得:x=60°,
∴∠AOC=60°,
∴∠BOD=60°,
∵OE⊥AB,
∴∠EOB=90°,
∴∠EOD=∠EOB-∠BOD=90°-60°=30°.
23.【答案】解:
24.【答案】解:∵OE⊥CD于点O(已知),
∴∠EOD=90°(垂直的定义),
∵∠EOB=115°(已知),
∴∠DOB=∠EOB-∠EOD=115°-90°=25°.
∵直线AB,CD相交于点O(已知),
∴∠AOC=∠DOB=25°(对顶角相等).
故答案为:∠EOD=90°;垂直的定义;∠EOB-∠EOD;∠DOB;对顶角相等.
25.【答案】解:用三角板直接过点P、D作线段的垂线,延长AB,用三角板直接过点F作线段延长线的垂线,则直线l、直线m、直线n即为所求,如图所示:
26.【答案】(1)解:利用直角三角板和直尺作图如下:
(2)解:利用直尺连接,作图如下:
(3);垂线段最短
27.【答案】(1)解:由邻补角的定义,得∠AOC+∠BOC=180°,
∵∠BOC=4∠AOC,
∴4∠AOC+∠AOC=180°,
∴∠AOC=36°,
由对顶角相等,得
∠BOD=∠AOC=36°;
(2)解:ON⊥CD,理由如下:
∵OM⊥AB,
∴∠AOM=90°,
∴∠1+∠AOC=90°,
∵∠1=∠2,
∴∠2+∠AOC=90°,
即∠NOC=90°,
∴ON⊥CD.
28.【答案】(1)解:OC平分,,
,
,
,
又,
;
(2)解:OE平分,理由如下:
平分,,
,
又,
;
平分.
