七年级下册人教版9.3一元一次不等式(组)课件(共23张PPT)
文档属性
| 名称 | 七年级下册人教版9.3一元一次不等式(组)课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 08:33:49 | ||
图片预览







文档简介
(共23张PPT)
2023中考数学一轮复习
一元一次不等式(组)
数学可以很简单
【复习目标】
1、掌握一次不等式的性质及解法
2、掌握一次不等式组解集的取值方法
3、掌握不等式在中考中的实际应用
考点一 一元一次不等式
1.(2022吉林)
A.
2.(2022宿迁)如果
A.
C.
中考真题
D
A
考点一 一元一次不等式
表示不等关系的式子叫做不等式。(表示不等关系的常用符号:≠,<,>)。
你能叙述不等式的基本性质吗?
不等式的基本性质
(1)不等式的两边都加上(或减去)同一个数,不等号方向不改变,如a> b, c为实数 a±c>b±c.
考点一 一元一次不等式
【满分技法】 使用不等式的性质3时,注意改变不等号的方向
(2)不等式两边都乘以(或除以)同一个正数,不等号方向不变,如a>b, c>0 ac>bc .
(3)不等式两边都乘以(或除以)同一个负数,不等号方向改变,如a>b,c<0 ac<bc .
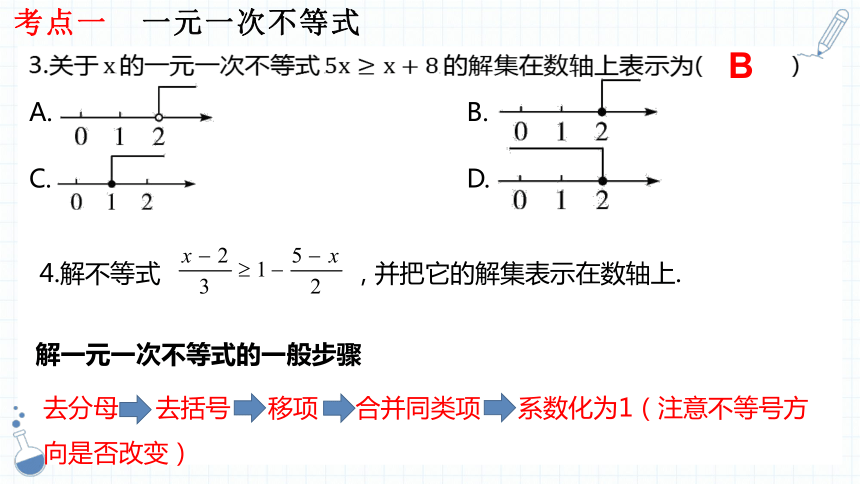
3.关于
考点一 一元一次不等式
A.&1& B.&2&
C.&3& D.&4&
B
解一元一次不等式的一般步骤
去分母 去括号 移项 合并同类项 系数化为1(注意不等号方向是否改变)
4.解不等式 , 并把它的解集表示在数轴上.
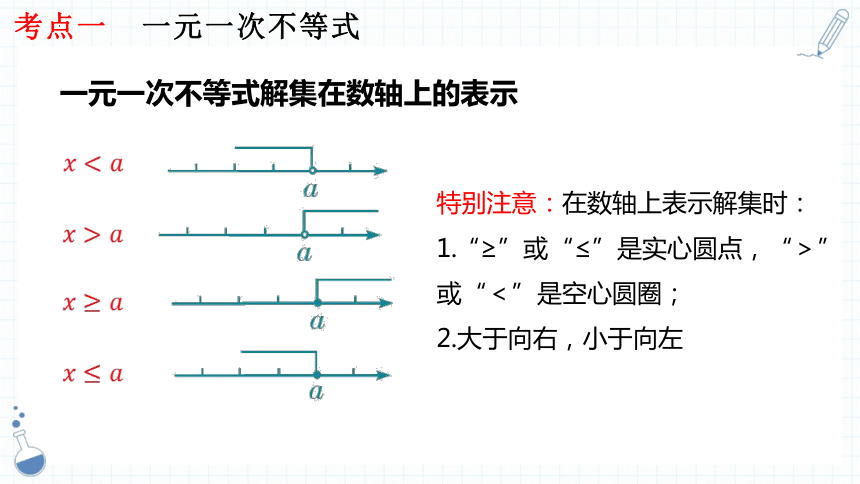
一元一次不等式解集在数轴上的表示
考点一 一元一次不等式
特别注意:在数轴上表示解集时:
1.“≥”或“≤”是实心圆点,“>”
或“<”是空心圆圈;
2.大于向右,小于向左
中考真题
考点一 一元一次不等式
6.(2022泸州)若方程
5.《指导与训练》P26--举一反三1
不等式(a-2)x>a-2 的解集是x>1,则a的取值范围是________.
a>2
考点二 一元一次不等式组
中考真题
考点二 一元一次不等式组
1.(2022十堰)关于
图所示,则该不等式组的解集为__________.
2.不等式组 的解集在数轴上表示为( )
C
3-x>1
一元一次不等式组的解集情况
考点二 一元一次不等式组
无解
同大取大
同小取小
大小、小大中间找
小小、大大取不了
3.(2022滨州)把不等式组表示出来,正确的为( )
A.&5& B.&6&
C.&7& D.&8&
中考真题
C
考点二 一元一次不等式组
4.(2022绥化)不等式组
_______.
考点三 一元一次不等式(组)
的应用
考点三 一元一次不等式(组)的应用
解题步骤:
①审:认真审题,分清已知量,未知量及其关系,找出题中的不等关系;
②设:用字母表示未知数;
③列:根据题意列出不等式(组);
④解:解不等式(组),在解集中找出符合题意的解;
⑤答:完整并准确的写出答案.
考点三 一元一次不等式(组)的应用
1、某次知识竞赛共有20道题,答对一题得10分,答错或不答每题扣
5分.小娜得分超过了90分,设她答对了x道题,则根据题意列不等式正确的是( )
《指导与训练》P29--热身回顾-2题
B
考点三 一元一次不等式(组)的应用
2.某产品生产车间有工人10名,已知每名工人每天可生产甲种产品12个或乙种产品10个,且每生产一个甲种产品可获利润100元,每生产一个乙种产品可获利润180元.如果要使此车间每天所获利润不低于15600元,你认为至少要派多少名工人去生产乙种产品才合适?
∴至少要派6名工人去生产乙种产品才合适
解:至少要派x名工人去生产乙种产品,则派(10-x)名工人去 生产甲种产品.由题意得:
解得:
《指导与训练》P29--例2
考点三 一元一次不等式(组)的应用
举一反三:小明准备用60元买甲、乙两种笔记本共12本.已知甲种笔记本每本6元,乙种笔记本每本3元,问:小明最多能买多少本甲种笔记本?
解:设购买甲种笔记本x本,乙种笔记本(12-x)本.
依题意,得
6x+3(12-x)≤60.
解得x≤8.
答:小明最多能买8本甲种笔记本.
《指导与训练》P29--举一反三2
课堂小结
谈谈本节课的收获?
一、 一元一次不等式
二、 一元一次不等式组
三、 一元一次不等式(组)的应用
一次不
等式与
一次不
等式组
一元一次不等
式(组)的解法
及解集表示
一元一次
不等式的
实际应用
解一元一
次不等式
解一元一次
不等式组
一般步骤
解集在数
轴上的表示
解法
解集的类
型及表示
列不等式解应用题的基本步骤
解决不等式的实际应用问题时,
常见的关键词与不等号的对比表
不等
式的
性质
性质2:如果a>b,并且c>0,
那么
性质1:如果a>b,那么
性质3:如果a>b,并且c<0,
那么
【知识图谱】
能力提升
1、(指导与训练P29-5)若关于x的不等式3x+1<m的正整数
解是1,2,3,则整数m的最大值是_____.
举一反三:(指导与训练P29)已知不等式2x-m<3(x+1)的负整数
解只有四个,则m的取值范围是______.
1<m≤2
13
能力提升
2、(指导与训练P29)若a使关于x的不等式组 ,有且
仅有四个整数解,则a的取值范围是________.
{
举一反三:(指导与训练P30-2)若关于x的不等式组 ,
仅有3个整数解,则a的取值范围是________.
{
-3≤a<-2
-4<a≤3
达标训练
《指导与训练》P27---达标训练
布置作业:
必做:《指导与训练》P27、P30--达标训练.
选做:《指导与训练》P32--方程与不等式.
2023中考数学一轮复习
一元一次不等式(组)
数学可以很简单
【复习目标】
1、掌握一次不等式的性质及解法
2、掌握一次不等式组解集的取值方法
3、掌握不等式在中考中的实际应用
考点一 一元一次不等式
1.(2022吉林)
A.
2.(2022宿迁)如果
A.
C.
中考真题
D
A
考点一 一元一次不等式
表示不等关系的式子叫做不等式。(表示不等关系的常用符号:≠,<,>)。
你能叙述不等式的基本性质吗?
不等式的基本性质
(1)不等式的两边都加上(或减去)同一个数,不等号方向不改变,如a> b, c为实数 a±c>b±c.
考点一 一元一次不等式
【满分技法】 使用不等式的性质3时,注意改变不等号的方向
(2)不等式两边都乘以(或除以)同一个正数,不等号方向不变,如a>b, c>0 ac>bc .
(3)不等式两边都乘以(或除以)同一个负数,不等号方向改变,如a>b,c<0 ac<bc .
3.关于
考点一 一元一次不等式
A.&1& B.&2&
C.&3& D.&4&
B
解一元一次不等式的一般步骤
去分母 去括号 移项 合并同类项 系数化为1(注意不等号方向是否改变)
4.解不等式 , 并把它的解集表示在数轴上.
一元一次不等式解集在数轴上的表示
考点一 一元一次不等式
特别注意:在数轴上表示解集时:
1.“≥”或“≤”是实心圆点,“>”
或“<”是空心圆圈;
2.大于向右,小于向左
中考真题
考点一 一元一次不等式
6.(2022泸州)若方程
5.《指导与训练》P26--举一反三1
不等式(a-2)x>a-2 的解集是x>1,则a的取值范围是________.
a>2
考点二 一元一次不等式组
中考真题
考点二 一元一次不等式组
1.(2022十堰)关于
图所示,则该不等式组的解集为__________.
2.不等式组 的解集在数轴上表示为( )
C
3-x>1
一元一次不等式组的解集情况
考点二 一元一次不等式组
无解
同大取大
同小取小
大小、小大中间找
小小、大大取不了
3.(2022滨州)把不等式组
A.&5& B.&6&
C.&7& D.&8&
中考真题
C
考点二 一元一次不等式组
4.(2022绥化)不等式组
_______.
考点三 一元一次不等式(组)
的应用
考点三 一元一次不等式(组)的应用
解题步骤:
①审:认真审题,分清已知量,未知量及其关系,找出题中的不等关系;
②设:用字母表示未知数;
③列:根据题意列出不等式(组);
④解:解不等式(组),在解集中找出符合题意的解;
⑤答:完整并准确的写出答案.
考点三 一元一次不等式(组)的应用
1、某次知识竞赛共有20道题,答对一题得10分,答错或不答每题扣
5分.小娜得分超过了90分,设她答对了x道题,则根据题意列不等式正确的是( )
《指导与训练》P29--热身回顾-2题
B
考点三 一元一次不等式(组)的应用
2.某产品生产车间有工人10名,已知每名工人每天可生产甲种产品12个或乙种产品10个,且每生产一个甲种产品可获利润100元,每生产一个乙种产品可获利润180元.如果要使此车间每天所获利润不低于15600元,你认为至少要派多少名工人去生产乙种产品才合适?
∴至少要派6名工人去生产乙种产品才合适
解:至少要派x名工人去生产乙种产品,则派(10-x)名工人去 生产甲种产品.由题意得:
解得:
《指导与训练》P29--例2
考点三 一元一次不等式(组)的应用
举一反三:小明准备用60元买甲、乙两种笔记本共12本.已知甲种笔记本每本6元,乙种笔记本每本3元,问:小明最多能买多少本甲种笔记本?
解:设购买甲种笔记本x本,乙种笔记本(12-x)本.
依题意,得
6x+3(12-x)≤60.
解得x≤8.
答:小明最多能买8本甲种笔记本.
《指导与训练》P29--举一反三2
课堂小结
谈谈本节课的收获?
一、 一元一次不等式
二、 一元一次不等式组
三、 一元一次不等式(组)的应用
一次不
等式与
一次不
等式组
一元一次不等
式(组)的解法
及解集表示
一元一次
不等式的
实际应用
解一元一
次不等式
解一元一次
不等式组
一般步骤
解集在数
轴上的表示
解法
解集的类
型及表示
列不等式解应用题的基本步骤
解决不等式的实际应用问题时,
常见的关键词与不等号的对比表
不等
式的
性质
性质2:如果a>b,并且c>0,
那么
性质1:如果a>b,那么
性质3:如果a>b,并且c<0,
那么
【知识图谱】
能力提升
1、(指导与训练P29-5)若关于x的不等式3x+1<m的正整数
解是1,2,3,则整数m的最大值是_____.
举一反三:(指导与训练P29)已知不等式2x-m<3(x+1)的负整数
解只有四个,则m的取值范围是______.
1<m≤2
13
能力提升
2、(指导与训练P29)若a使关于x的不等式组 ,有且
仅有四个整数解,则a的取值范围是________.
{
举一反三:(指导与训练P30-2)若关于x的不等式组 ,
仅有3个整数解,则a的取值范围是________.
{
-3≤a<-2
-4<a≤3
达标训练
《指导与训练》P27---达标训练
布置作业:
必做:《指导与训练》P27、P30--达标训练.
选做:《指导与训练》P32--方程与不等式.
