北师大版八年级下册3.2图形的旋转(第一课时)课件(共22张PPT)
文档属性
| 名称 | 北师大版八年级下册3.2图形的旋转(第一课时)课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 08:47:21 | ||
图片预览






文档简介
(共22张PPT)
主讲:XXX
3.2 图形的旋转(第一课时)
北师大版八年级 下册
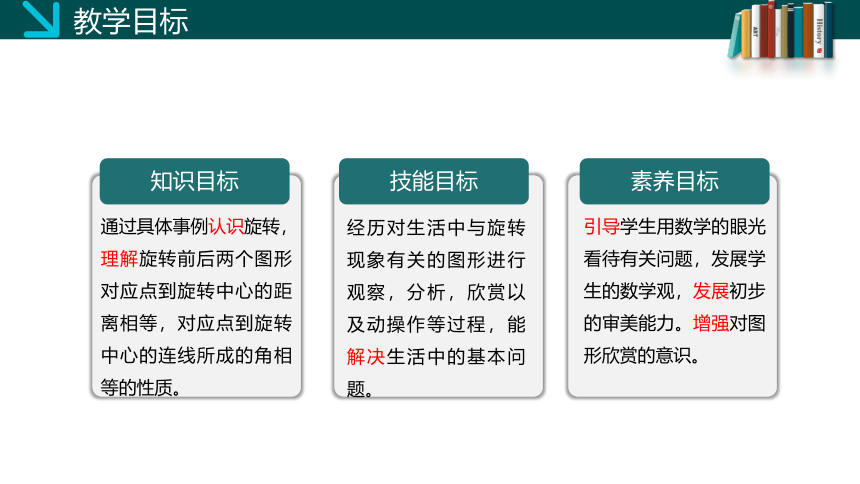
教学目标
素养目标
技能目标
知识目标
通过具体事例认识旋转,理解旋转前后两个图形对应点到旋转中心的距离相等,对应点到旋转中心的连线所成的角相等的性质。
经历对生活中与旋转现象有关的图形进行观察,分析,欣赏以及动操作等过程,能解决生活中的基本问题。
引导学生用数学的眼光看待有关问题,发展学生的数学观,发展初步的审美能力。增强对图形欣赏的意识。
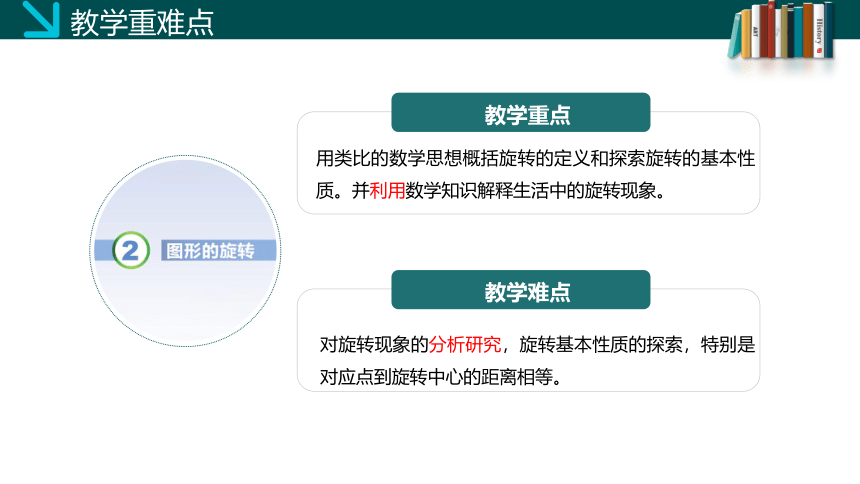
教学重难点
教学重点
教学难点
用类比的数学思想概括旋转的定义和探索旋转的基本性质。并利用数学知识解释生活中的旋转现象。
对旋转现象的分析研究,旋转基本性质的探索,特别是对应点到旋转中心的距离相等。
创设情境 引入新课
思考1:
观察钟表时针、分针、秒针的运动.
创设情境 引入新课
思考2:
观察风车运动.
创设情境 引入新课
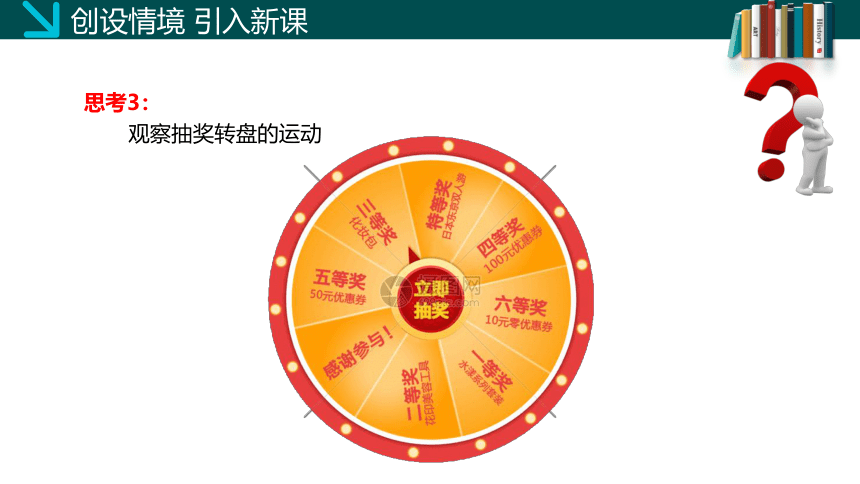
思考3:
观察抽奖转盘的运动
创设情境 引入新课
思考3:
观察秋千的运动。
典例探究 深化新知
问题1:
它们都做什么运动?
旋转运动
问题2:
它们的形状、大小在运动前后是否发生了改变?什么改变了?
形状、大小都没有改变。位置改变了
典例探究 深化新知
问题3:
怎样来定义这种图形变换?
把时针当成一个图形,那么它可以绕着中心固定点转动一定角度.
钟表的指针在不停地转动,从12时到8时,时针转动了______度.
240
归纳总结 认知升华
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转.
你能否描述一下什么叫旋转?
这个定点称为旋转中心.
转动的角称为旋转角.
转动的方向分为顺时针与逆时针.
如果图形上的点P经过旋转变为点P',这两个点叫做这个旋转的对应点.
O
P′
P
旋转中心
旋转角
对应点
典例探究 深化新知
例1
如图,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:
(1)旋转中心是什么 旋转角是什么
(2)经过旋转,点A, B分别移动到什么位置?
(3)AO 与 DO 的长有什么关系 BO 与 EO 呢
(4)∠AOD与∠BOE有什么大小关系
点O
∠AOD
A
O
C
D
F
E
B
或∠BOE
点D
点E
相等
相等
相等
典例探究 深化新知
例2
如图所示,△ABC是直角三角形,延长AB到D,使BD=BC,在BC上取BE=AB,连接DE.△ABC旋转后能与△EBD重合,那么:旋转中心是______;旋转的角度是________;AC的对应边是________∠A的对应角是________;点C的对应点是________.
点B
90°
ED
∠BED
点D
归纳总结 认知升华
你能否发现旋转的性质?
一个改变:
位置改变
两个相同:
方向相同、旋转角度相同
两个不变:
形状不变、大小不变。
1.旋转图形的任意一对对应点与旋转中心的连线所成的角都是旋转角.
2.旋转图形的任意一对对应点到旋转中心的距离相等.
一个图形由一个位置旋转到另一个位置,固定不动的点是旋转中心,互换位置的点是对应点,互换位置的边是对应边,对应边的夹角是旋转角.
体验新知 学以致用
1.
在下图的四个三角形中,哪个不能由△ABC经过平移或旋转得到?
图(2)
体验新知 学以致用
2.
如图,四边形ABCD经过旋转后与四边形ADEF重合.
(1)指出这一旋转的旋转中心和旋转角;
(2)写出图中相等的线段和相等的角.
解:(1)旋转中心为A;
旋转角有∠BAD,∠CAE,∠DAF.
(2)相等的线段:AB=AD,AC=AE,AD=AF,
BC=DE,CD=EF,AB=AF;
相等的角:∠BAC=∠DAE,
∠BAD=∠CAE=∠DAF,∠CAD=∠EAF,
∠ABC=∠ADE,∠ADC=∠AFE,∠BCD=∠DEF
∠BCA=∠DEA,∠ACD=∠AEF.
体验新知 学以致用
3.
图案可以看作是一个菱形通过几次旋转得到的?
每次旋转了多少角度?
答:旋转5次得到,旋转角度分别等于60°, 120°, 180°, 240°, 300°.
体验新知 学以致用
4.
如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转的角度为( )
A.30°
B.45°
C.90°
D.135°
分析:对应点与旋转中心的连线的夹角,就是旋转角,由图可知,OB、OD是对应边,∠BOD是旋转角,所以,旋转角为90°.故选C.
体验新知 学以致用
5.
如图,你能绕点O旋转,使得线段AB与线段CD重合吗?为什么?
分析:旋转前后对应点到旋转中心的距离相等,而图中OA与OC不相等,OB与OD也不相等。
体验新知 学以致用
6.
旋转图案欣赏
归纳总结 认知升华
概念:在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。这个定点称为旋转中心,转动的角称为旋转角。
思想方法
逆向思维,转化思维。
文字语言-图形语言-符号语言的互相转化.
数形结合思想,数学建模.
图形的旋转
旋转的性质:
(1)对应点与旋转中心的连线所成的角都是旋转角;
(2)对应点到旋转中心的距离相等;
(3)旋转不改变图形的形状和大小;
(4)图形位置改变。
布置作业 减负增效
习题3.4第1、2题
非学无以广才,非志无以成学。
主讲:XXX
主讲:XXX
3.2 图形的旋转(第一课时)
北师大版八年级 下册
教学目标
素养目标
技能目标
知识目标
通过具体事例认识旋转,理解旋转前后两个图形对应点到旋转中心的距离相等,对应点到旋转中心的连线所成的角相等的性质。
经历对生活中与旋转现象有关的图形进行观察,分析,欣赏以及动操作等过程,能解决生活中的基本问题。
引导学生用数学的眼光看待有关问题,发展学生的数学观,发展初步的审美能力。增强对图形欣赏的意识。
教学重难点
教学重点
教学难点
用类比的数学思想概括旋转的定义和探索旋转的基本性质。并利用数学知识解释生活中的旋转现象。
对旋转现象的分析研究,旋转基本性质的探索,特别是对应点到旋转中心的距离相等。
创设情境 引入新课
思考1:
观察钟表时针、分针、秒针的运动.
创设情境 引入新课
思考2:
观察风车运动.
创设情境 引入新课
思考3:
观察抽奖转盘的运动
创设情境 引入新课
思考3:
观察秋千的运动。
典例探究 深化新知
问题1:
它们都做什么运动?
旋转运动
问题2:
它们的形状、大小在运动前后是否发生了改变?什么改变了?
形状、大小都没有改变。位置改变了
典例探究 深化新知
问题3:
怎样来定义这种图形变换?
把时针当成一个图形,那么它可以绕着中心固定点转动一定角度.
钟表的指针在不停地转动,从12时到8时,时针转动了______度.
240
归纳总结 认知升华
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转.
你能否描述一下什么叫旋转?
这个定点称为旋转中心.
转动的角称为旋转角.
转动的方向分为顺时针与逆时针.
如果图形上的点P经过旋转变为点P',这两个点叫做这个旋转的对应点.
O
P′
P
旋转中心
旋转角
对应点
典例探究 深化新知
例1
如图,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:
(1)旋转中心是什么 旋转角是什么
(2)经过旋转,点A, B分别移动到什么位置?
(3)AO 与 DO 的长有什么关系 BO 与 EO 呢
(4)∠AOD与∠BOE有什么大小关系
点O
∠AOD
A
O
C
D
F
E
B
或∠BOE
点D
点E
相等
相等
相等
典例探究 深化新知
例2
如图所示,△ABC是直角三角形,延长AB到D,使BD=BC,在BC上取BE=AB,连接DE.△ABC旋转后能与△EBD重合,那么:旋转中心是______;旋转的角度是________;AC的对应边是________∠A的对应角是________;点C的对应点是________.
点B
90°
ED
∠BED
点D
归纳总结 认知升华
你能否发现旋转的性质?
一个改变:
位置改变
两个相同:
方向相同、旋转角度相同
两个不变:
形状不变、大小不变。
1.旋转图形的任意一对对应点与旋转中心的连线所成的角都是旋转角.
2.旋转图形的任意一对对应点到旋转中心的距离相等.
一个图形由一个位置旋转到另一个位置,固定不动的点是旋转中心,互换位置的点是对应点,互换位置的边是对应边,对应边的夹角是旋转角.
体验新知 学以致用
1.
在下图的四个三角形中,哪个不能由△ABC经过平移或旋转得到?
图(2)
体验新知 学以致用
2.
如图,四边形ABCD经过旋转后与四边形ADEF重合.
(1)指出这一旋转的旋转中心和旋转角;
(2)写出图中相等的线段和相等的角.
解:(1)旋转中心为A;
旋转角有∠BAD,∠CAE,∠DAF.
(2)相等的线段:AB=AD,AC=AE,AD=AF,
BC=DE,CD=EF,AB=AF;
相等的角:∠BAC=∠DAE,
∠BAD=∠CAE=∠DAF,∠CAD=∠EAF,
∠ABC=∠ADE,∠ADC=∠AFE,∠BCD=∠DEF
∠BCA=∠DEA,∠ACD=∠AEF.
体验新知 学以致用
3.
图案可以看作是一个菱形通过几次旋转得到的?
每次旋转了多少角度?
答:旋转5次得到,旋转角度分别等于60°, 120°, 180°, 240°, 300°.
体验新知 学以致用
4.
如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转的角度为( )
A.30°
B.45°
C.90°
D.135°
分析:对应点与旋转中心的连线的夹角,就是旋转角,由图可知,OB、OD是对应边,∠BOD是旋转角,所以,旋转角为90°.故选C.
体验新知 学以致用
5.
如图,你能绕点O旋转,使得线段AB与线段CD重合吗?为什么?
分析:旋转前后对应点到旋转中心的距离相等,而图中OA与OC不相等,OB与OD也不相等。
体验新知 学以致用
6.
旋转图案欣赏
归纳总结 认知升华
概念:在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。这个定点称为旋转中心,转动的角称为旋转角。
思想方法
逆向思维,转化思维。
文字语言-图形语言-符号语言的互相转化.
数形结合思想,数学建模.
图形的旋转
旋转的性质:
(1)对应点与旋转中心的连线所成的角都是旋转角;
(2)对应点到旋转中心的距离相等;
(3)旋转不改变图形的形状和大小;
(4)图形位置改变。
布置作业 减负增效
习题3.4第1、2题
非学无以广才,非志无以成学。
主讲:XXX
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
