人教版六年级数学上册 第三单元第6课时《圆锥的体积》精品教学方案
文档属性
| 名称 | 人教版六年级数学上册 第三单元第6课时《圆锥的体积》精品教学方案 | 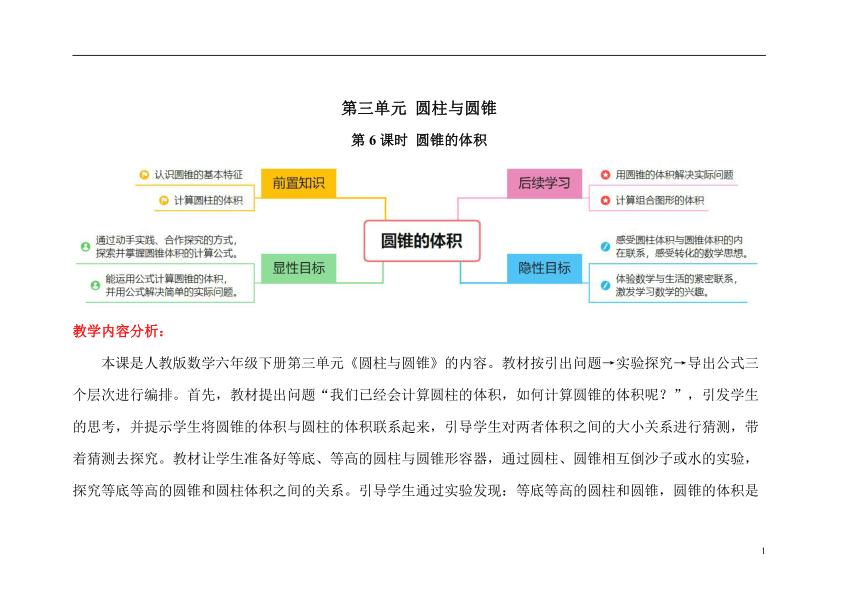 | |
| 格式 | docx | ||
| 文件大小 | 125.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-21 15:27:02 | ||
图片预览


文档简介
第三单元 圆柱与圆锥
第6课时 圆锥的体积
教学内容分析:
本课是人教版数学六年级下册第三单元《圆柱与圆锥》的内容。教材按引出问题→实验探究→导出公式三个层次进行编排。首先,教材提出问题“我们已经会计算圆柱的体积,如何计算圆锥的体积呢?”,引发学生的思考,并提示学生将圆锥的体积与圆柱的体积联系起来,引导学生对两者体积之间的大小关系进行猜测,带着猜测去探究。教材让学生准备好等底、等高的圆柱与圆锥形容器,通过圆柱、圆锥相互倒沙子或水的实验,探究等底等高的圆锥和圆柱体积之间的关系。引导学生通过实验发现:等底等高的圆柱和圆锥,圆锥的体积是圆柱体积的,由此得出圆锥体积的计算公式。例3是圆锥体积计算公式的简单应用,题目给出了圆锥形沙堆的底面直径和高,求沙堆的体积和质量。学生在应用公式时需要注意合理利用题目中给出的信息,如要把底面直径转化为半径再计算,增强学生灵活应用圆锥体积计算公式的能力。
教学目标:
1. 通过动手实践、合作探究的方式,探索并掌握圆锥体积的计算公式,能运用公式计算圆锥的体积,以及能用公式解决简单的实际问题。
2. 感受圆柱体积与圆锥体积的内在联系,感受转化的数学思想。
3. 体验数学与生活的紧密联系,激发学习数学的兴趣。
教学重点:
理解和掌握圆锥体积的计算公式,并能解决实际问题。
教学难点:
圆锥体积公式的推导方法。
教学过程:
教学环节 教师活动 学生活动 设计意图
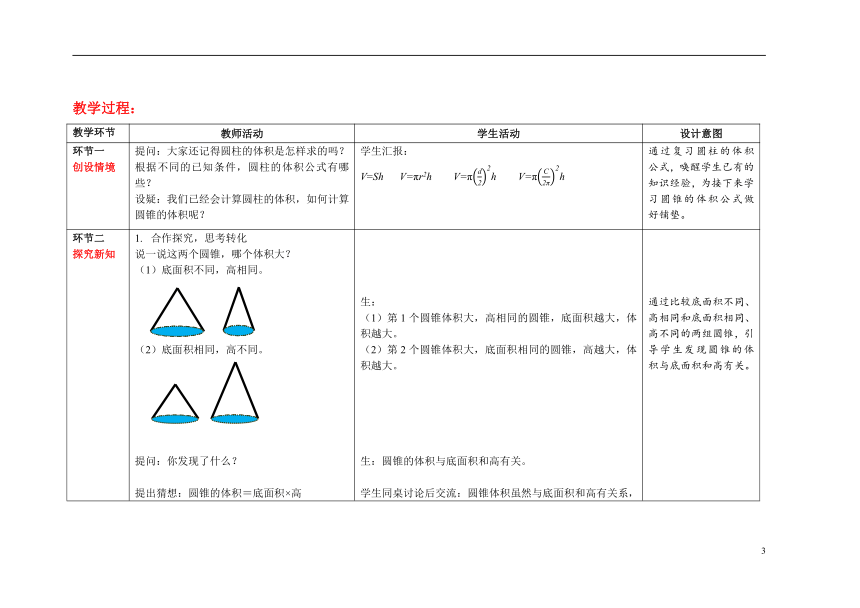
环节一 创设情境 提问:大家还记得圆柱的体积是怎样求的吗?根据不同的已知条件,圆柱的体积公式有哪些? 设疑:我们已经会计算圆柱的体积,如何计算圆锥的体积呢? 学生汇报: V=Sh V=πr2h V=πh V=πh 通过复习圆柱的体积公式,唤醒学生已有的知识经验,为接下来学习圆锥的体积公式做好铺垫。
环节二 探究新知 合作探究,思考转化 说一说这两个圆锥,哪个体积大? 底面积不同,高相同。 底面积相同,高不同。 提问:你发现了什么? 提出猜想:圆锥的体积=底面积×高 引导学生思考:等底等高的圆锥的体积和圆柱的体积有没有关系呢? 圆锥的体积和圆柱的体积之间存在着什么样的关系? 研究关联,推导公式 下面通过实验,探究圆锥和圆柱体积之间的关系。 各组准备好等底、等高的圆柱、圆锥形容器。 将圆锥形容器装满水后倒入圆柱容器,重复多次。 通过这个实验:你发现了什么?圆锥体积和圆柱体积之间有什么样的关系? 公式运用,解决问题 工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5 t,这堆沙子大约重多少吨? 提问: ①要先算什么,再算什么? ②,题目中告诉我们高是1.5 m,但是没有直接告诉我们底面积是多少,怎么求底面积呢? 学生独立完成解答,教师巡视,对有困难的学生进行指导。 生: 第1个圆锥体积大,高相同的圆锥,底面积越大,体积越大。 第2个圆锥体积大,底面积相同的圆锥,高越大,体积越大。 生:圆锥的体积与底面积和高有关。 学生同桌讨论后交流:圆锥体积虽然与底面积和高有关系,但圆锥的上面尖尖的,“底面积×高”不是圆锥的体积,而是圆柱的体积。 学生自由发言。 生:圆柱的底面是圆,圆锥的底面也是圆;如果从一个圆柱上底面的圆心和下底面圆周上的每一点连起来,就可以得到一个和圆柱等底等高的圆锥。 学生猜测两者体积之间的关系。 学生动手实验,进行探究。 学生小组讨论、交流汇报。 生: ①将圆锥形容器装满水倒入圆柱容器3次后,正好倒满。 ②3个圆锥的体积=1个圆柱体积 ③圆锥体积等于与它等底等高圆柱体积的 ④ 生: 先求沙子的体积,也就是求圆锥的体积;再求沙子的质量,用体积×沙子每立方米的质量。 ② 要把直径转化为半径,再求出底面积。 学生独立完成。 沙堆的底面积:=12.56(m ) 沙堆的体积:×12.56×1.5=6.28(m ) 沙堆的质量:6.28×1.5=9.42(t) 答:这堆沙子的体积大约是6.28 m3,大约重9.42 t 通过比较底面积不同、高相同和底面积相同、高不同的两组圆锥,引导学生发现圆锥的体积与底面积和高有关。 将圆锥的体积与圆柱的体积联系起来,引导学生对两者体积之间的大小关系进行猜测,带着猜测去探究。 在学生猜想的基础上,用实验探究的方法加以验证,让学生经历圆锥体积计算公式的推导过程,提高发现和提出问题的意识。 引导学生合理运用信息,自主解决问题,加深对圆锥体积计算公式的理解,提高学生灵活应用圆锥体积计算公式的能力。
环节三 巩固新知 判断对错,对的画“√”,错的画“×”。 (1)圆锥的体积等于圆柱体积的。 ( ) (2)圆柱的体积大于与它等底等高的圆锥的体积。 ( ) (3)圆锥的高是圆柱的高的3倍,它们的体积一定相等。 ( ) 一个圆锥形的零件,底面积是19 cm2,高12 cm。这个零件的体积是多少? 一个用钢铸造成的圆锥形铅锤,底面直径是4 cm,高6cm。每立方厘米钢大约重7.9 g。这个铅锤重多少克?(得数保留整数。) 一个圆锥的底面周长是31.4 cm,高是9 cm。它的体积是多少? 学生判断对错并说明原因: (1)×,圆柱和圆柱不一定是等底等高的。 (2)√ (3)×,圆柱和圆锥的底面积不一定是相等的。 学生独立思考后全班交流。 ×19 ×12=76(cm ) 答:这个零件的体积是76 cm 。 学生小组讨论后交流汇报。 铅锤底面积: 3.14×(4÷2)2=3.14×4=12.56(cm2) 铅锤的体积: ×12.56×5≈25.09(cm3) 铅锤的质量: 25.09×7.9≈198(g) 答:这个铅锤重198克。 学生独立思考完成。 ×3.14×(31.4÷3.14÷2)2×9=235.5(cm3) 答:它的体积是235.5 cm3。 第1题是有关圆锥与圆柱体积关系的判断题,使学生进一步明确只有等底等高的圆柱与圆锥的体积才存在3倍的关系。 第2、3、4题中提供了不同的信息形式,巩固圆锥体积的计算,如第2题直接给出底面积,第3题给出的是底面直径,第4题给出的是底面周长,其中第3题算出圆锥的体积后,还要再计算铅锤的质量,提高学生理解、分析、解决实际问题的能力。
环节四 课堂小结 你有什么收获? 生1:我学会了圆锥的体积。 生2:圆锥体积等于与它等底等高圆柱体积的。 生3:。 鼓励学生畅谈自己的收获和体会,有哪些认知上的冲突,遇到问题是如何解决的。
环节五 拓展延伸 如图,把一个体积是73 dm 的圆柱形木块,削成两个顶点相连的完全相同的圆锥形木块,形成“沙漏”状,那么每个圆锥的体积是多少立方分米? 生:72×÷2 =24÷2 =12(dm3) 答:每个圆锥的体积是12dm 。 在情境中,进一步感受圆锥和圆柱之间的关系,通过图形之间高、底面的对应,解决体积问题。
环节六 课后活动 观察生活中的圆锥形,你能计算它们的体积吗,和小伙伴们一起交流一下吧! 布置一个小活动,学生从活动经验或感受中获得自己的经验。
1
第6课时 圆锥的体积
教学内容分析:
本课是人教版数学六年级下册第三单元《圆柱与圆锥》的内容。教材按引出问题→实验探究→导出公式三个层次进行编排。首先,教材提出问题“我们已经会计算圆柱的体积,如何计算圆锥的体积呢?”,引发学生的思考,并提示学生将圆锥的体积与圆柱的体积联系起来,引导学生对两者体积之间的大小关系进行猜测,带着猜测去探究。教材让学生准备好等底、等高的圆柱与圆锥形容器,通过圆柱、圆锥相互倒沙子或水的实验,探究等底等高的圆锥和圆柱体积之间的关系。引导学生通过实验发现:等底等高的圆柱和圆锥,圆锥的体积是圆柱体积的,由此得出圆锥体积的计算公式。例3是圆锥体积计算公式的简单应用,题目给出了圆锥形沙堆的底面直径和高,求沙堆的体积和质量。学生在应用公式时需要注意合理利用题目中给出的信息,如要把底面直径转化为半径再计算,增强学生灵活应用圆锥体积计算公式的能力。
教学目标:
1. 通过动手实践、合作探究的方式,探索并掌握圆锥体积的计算公式,能运用公式计算圆锥的体积,以及能用公式解决简单的实际问题。
2. 感受圆柱体积与圆锥体积的内在联系,感受转化的数学思想。
3. 体验数学与生活的紧密联系,激发学习数学的兴趣。
教学重点:
理解和掌握圆锥体积的计算公式,并能解决实际问题。
教学难点:
圆锥体积公式的推导方法。
教学过程:
教学环节 教师活动 学生活动 设计意图
环节一 创设情境 提问:大家还记得圆柱的体积是怎样求的吗?根据不同的已知条件,圆柱的体积公式有哪些? 设疑:我们已经会计算圆柱的体积,如何计算圆锥的体积呢? 学生汇报: V=Sh V=πr2h V=πh V=πh 通过复习圆柱的体积公式,唤醒学生已有的知识经验,为接下来学习圆锥的体积公式做好铺垫。
环节二 探究新知 合作探究,思考转化 说一说这两个圆锥,哪个体积大? 底面积不同,高相同。 底面积相同,高不同。 提问:你发现了什么? 提出猜想:圆锥的体积=底面积×高 引导学生思考:等底等高的圆锥的体积和圆柱的体积有没有关系呢? 圆锥的体积和圆柱的体积之间存在着什么样的关系? 研究关联,推导公式 下面通过实验,探究圆锥和圆柱体积之间的关系。 各组准备好等底、等高的圆柱、圆锥形容器。 将圆锥形容器装满水后倒入圆柱容器,重复多次。 通过这个实验:你发现了什么?圆锥体积和圆柱体积之间有什么样的关系? 公式运用,解决问题 工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5 t,这堆沙子大约重多少吨? 提问: ①要先算什么,再算什么? ②,题目中告诉我们高是1.5 m,但是没有直接告诉我们底面积是多少,怎么求底面积呢? 学生独立完成解答,教师巡视,对有困难的学生进行指导。 生: 第1个圆锥体积大,高相同的圆锥,底面积越大,体积越大。 第2个圆锥体积大,底面积相同的圆锥,高越大,体积越大。 生:圆锥的体积与底面积和高有关。 学生同桌讨论后交流:圆锥体积虽然与底面积和高有关系,但圆锥的上面尖尖的,“底面积×高”不是圆锥的体积,而是圆柱的体积。 学生自由发言。 生:圆柱的底面是圆,圆锥的底面也是圆;如果从一个圆柱上底面的圆心和下底面圆周上的每一点连起来,就可以得到一个和圆柱等底等高的圆锥。 学生猜测两者体积之间的关系。 学生动手实验,进行探究。 学生小组讨论、交流汇报。 生: ①将圆锥形容器装满水倒入圆柱容器3次后,正好倒满。 ②3个圆锥的体积=1个圆柱体积 ③圆锥体积等于与它等底等高圆柱体积的 ④ 生: 先求沙子的体积,也就是求圆锥的体积;再求沙子的质量,用体积×沙子每立方米的质量。 ② 要把直径转化为半径,再求出底面积。 学生独立完成。 沙堆的底面积:=12.56(m ) 沙堆的体积:×12.56×1.5=6.28(m ) 沙堆的质量:6.28×1.5=9.42(t) 答:这堆沙子的体积大约是6.28 m3,大约重9.42 t 通过比较底面积不同、高相同和底面积相同、高不同的两组圆锥,引导学生发现圆锥的体积与底面积和高有关。 将圆锥的体积与圆柱的体积联系起来,引导学生对两者体积之间的大小关系进行猜测,带着猜测去探究。 在学生猜想的基础上,用实验探究的方法加以验证,让学生经历圆锥体积计算公式的推导过程,提高发现和提出问题的意识。 引导学生合理运用信息,自主解决问题,加深对圆锥体积计算公式的理解,提高学生灵活应用圆锥体积计算公式的能力。
环节三 巩固新知 判断对错,对的画“√”,错的画“×”。 (1)圆锥的体积等于圆柱体积的。 ( ) (2)圆柱的体积大于与它等底等高的圆锥的体积。 ( ) (3)圆锥的高是圆柱的高的3倍,它们的体积一定相等。 ( ) 一个圆锥形的零件,底面积是19 cm2,高12 cm。这个零件的体积是多少? 一个用钢铸造成的圆锥形铅锤,底面直径是4 cm,高6cm。每立方厘米钢大约重7.9 g。这个铅锤重多少克?(得数保留整数。) 一个圆锥的底面周长是31.4 cm,高是9 cm。它的体积是多少? 学生判断对错并说明原因: (1)×,圆柱和圆柱不一定是等底等高的。 (2)√ (3)×,圆柱和圆锥的底面积不一定是相等的。 学生独立思考后全班交流。 ×19 ×12=76(cm ) 答:这个零件的体积是76 cm 。 学生小组讨论后交流汇报。 铅锤底面积: 3.14×(4÷2)2=3.14×4=12.56(cm2) 铅锤的体积: ×12.56×5≈25.09(cm3) 铅锤的质量: 25.09×7.9≈198(g) 答:这个铅锤重198克。 学生独立思考完成。 ×3.14×(31.4÷3.14÷2)2×9=235.5(cm3) 答:它的体积是235.5 cm3。 第1题是有关圆锥与圆柱体积关系的判断题,使学生进一步明确只有等底等高的圆柱与圆锥的体积才存在3倍的关系。 第2、3、4题中提供了不同的信息形式,巩固圆锥体积的计算,如第2题直接给出底面积,第3题给出的是底面直径,第4题给出的是底面周长,其中第3题算出圆锥的体积后,还要再计算铅锤的质量,提高学生理解、分析、解决实际问题的能力。
环节四 课堂小结 你有什么收获? 生1:我学会了圆锥的体积。 生2:圆锥体积等于与它等底等高圆柱体积的。 生3:。 鼓励学生畅谈自己的收获和体会,有哪些认知上的冲突,遇到问题是如何解决的。
环节五 拓展延伸 如图,把一个体积是73 dm 的圆柱形木块,削成两个顶点相连的完全相同的圆锥形木块,形成“沙漏”状,那么每个圆锥的体积是多少立方分米? 生:72×÷2 =24÷2 =12(dm3) 答:每个圆锥的体积是12dm 。 在情境中,进一步感受圆锥和圆柱之间的关系,通过图形之间高、底面的对应,解决体积问题。
环节六 课后活动 观察生活中的圆锥形,你能计算它们的体积吗,和小伙伴们一起交流一下吧! 布置一个小活动,学生从活动经验或感受中获得自己的经验。
1
