人教版六年级数学上册 第四单元第11课时《单元综合复习》精品教学方案
文档属性
| 名称 | 人教版六年级数学上册 第四单元第11课时《单元综合复习》精品教学方案 |  | |
| 格式 | docx | ||
| 文件大小 | 227.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-21 15:33:46 | ||
图片预览



文档简介
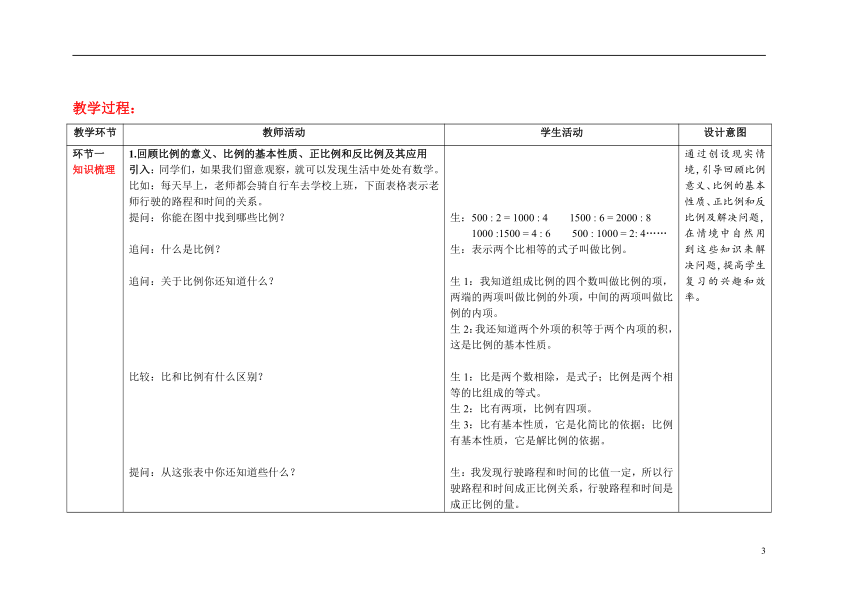
第四单元 比例
单元综合复习
教学内容分析:
本课是人教版六年级下册第四单元的单元复习课。通过前几节课的学习学生已经知道了什么是比例、比例的基本性质、正比例和反比例及它们的应用等。本节课对这部分知识进行梳理,引导学生自主整理单元知识,体验归纳整理、构建知识体系的方法。针对各知识点适当的设计了有层次的习题,习题紧扣生活,在解决生活中的实际问题中培养灵活解决问题的能力,并感受数学在生活中的应用价值。
教学目标:
1.回顾比例的有关知识,能用比例解决生活中的实际问题。
2.经历比和比例知识的整理过程,沟通知识间的联系,体验对比、归纳等方法,培养合作意识,增强学生学好数学的信心。
3.能运用比和比例的知识解决简单的实际问题,丰富解决问题的策略,积累解决问题的经验。
教学重点:
对比和比例的知识进行系统整理。
教学难点:
理清知识间的联系,构建知识网络。
教学过程:
教学环节 教师活动 学生活动 设计意图
环节一 知识梳理 1.回顾比例的意义、比例的基本性质、正比例和反比例及其应用 引入:同学们,如果我们留意观察,就可以发现生活中处处有数学。比如:每天早上,老师都会骑自行车去学校上班,下面表格表示老师行驶的路程和时间的关系。 提问:你能在图中找到哪些比例? 追问:什么是比例? 追问:关于比例你还知道什么? 比较:比和比例有什么区别? 提问:从这张表中你还知道些什么? 提问:老师7:20出发,7:40到达学校,老师家离学校有多远? 追问: 老师家到学校的路程一定,行驶的速度和时间又成什么比例,为什么? 2.回顾比例的应用、图形的放大与缩小 提问:这是老师按1:80的比例在校园拍摄的一张照片,如果老师照片上的身高是2厘米,那么你能算出老师的实际身高吗? 提问:其实校门口还有一位同学,能看清他的样子吗? 追问:那怎么办? 出示:按7:1放大。 生:500 : 2 = 1000 : 4 1500 : 6 = 2000 : 8 1000 :1500 = 4 : 6 500 : 1000 = 2: 4…… 生:表示两个比相等的式子叫做比例。 生1:我知道组成比例的四个数叫做比例的项,两端的两项叫做比例的外项,中间的两项叫做比例的内项。 生2:我还知道两个外项的积等于两个内项的积,这是比例的基本性质。 生1:比是两个数相除,是式子;比例是两个相等的比组成的等式。 生2:比有两项,比例有四项。 生3:比有基本性质,它是化简比的依据;比例有基本性质,它是解比例的依据。 生:我发现行驶路程和时间的比值一定,所以行驶路程和时间成正比例关系,行驶路程和时间是成正比例的量。 生1:用算术法解决,根据“路程=速度×时间”,250×20=5000(米); 生2:可以用正比例解决问题, 设老师家到学校有x米, 500 : 2= x : 20 x =5000 答:老师家离学校5000米。 生:速度和时间成反比例关系,因为:速度×时间=路程(一定)。 生1:根据“图上距离:实际距离=1:80”,可以用解比例的方法解决问题。 解:设老师实际身高是x cm。 2:x=1:80 x=160 答:老师的实际身高是160 cm。 生2:根据“图上距离:实际距离=1:80”,推出“实际距离=图上距离÷ 2÷=160(cm) 答:老师实际身高是160 cm。 生:看不清。 生:按比例放大就能看清了。 通过创设现实情境,引导回顾比例意义、比例的基本性质、正比例和反比例及解决问题,在情境中自然用到这些知识来解决问题,提高学生复习的兴趣和效率。 将情境进行串联,由骑车到校切换到到达学校,并自然衔接到比例尺的复习及图形的放大与缩小,使知识整理更加有趣。
环节二 综合练习 1.填一填。 如果=y,那么x与y成( )比例;如果=y,那么x与y成( )比例。 在比例尺是6:1的平面图上量得零件的长为15 cm,零件的实际长是( )。 一个长6 cm,宽4 cm的长方形按1:2缩小,得到的图形的面积是( )cm 。 独立思考后反馈:你是怎么想的? 2.辨一辨。 下面各题中的两种量是否成比例关系?如果成比例关系,成什么比例关系? 长方体的高一定,体积和底面积。 圆的面积和它的半径。 长方形的周长一定,长和宽。 独立思考后反馈:你是怎么想的? 3.解决问题 (1)如图,长方形ABCD中,动点P沿着AB从A点运动到B点,三角形PAD的面积随着P点运动在不断地变化。 当PA=2 cm时,三角形PAD的面积是3 cm2,当PA=4.5 cm时, 三角形PAD的面积是多少平方厘米?(用比例解) 练习:独立思考解题。 反馈:你是怎么做的? (2)要给客厅铺地砖,如果用边长是6 dm的方砖,需要 80块;如果改用边长是8 dm的方砖,需要多少块?(用比例解) 练习:独立思考解题。 反馈:你是怎么做的? 小结:用比例解决问题,要先判断两个量成什么比例关系,再根据关系解决问题。 学生独立思考。 根据=y,可知=8,x与y成正比例; 根据=y,可知xy=8,x与y成反比例。 图上距离:实际距离=比例尺 解:设零件的实际长是x cm。 15:x=6:1 6x=15 x=2.5 (3)方法一: 缩小后长方形的长:6÷2=3(cm) 缩小后长方形的宽:4÷2=2(cm) 得到的图形的面积:3×2=6(cm ) 方法二: 原长方形面积:6×4=24(cm ) 缩小后的面积:24÷(2×2)=6(cm ) 成正比例,因为=高(一定)。 不成比例关系,=πr,比值不定。 (3)不成比例关系,长+宽=周长的一半(一定),长和宽的和一定,不成比例。 根据“三角形PAD∶PA=2×AD(一定)”可知三角形PAD的面积和PA成正比例关系。 解:设当PA=4.5 cm时,三角形PAD的面积是x cm 。 x∶4.5 = 3∶2 2x=13.5 x=6.75 答:设当PA=4.5 cm时,三角形PAD的面积是6.75 cm 。 根据“每块方砖面积×方砖数量=客厅面积(一定),可知每块方砖面积和方砖数量成反比例关系。 解:设需要x块。 8×8×x=6×6×80 8x=360 x=45 答:改用边长是8 dm的方砖,需要45块。 填一填是关于比例相关知识的基础练习,旨在熟练掌握。 辨一辨是判断两种量是否成比例关系,第2和第3题是典型错误,学生容易根据图形计算公式直接判断成比例关系,这两题意图从本质上理解如何判断两个量是否成比例关系。 这两道题要求用比例解决问题,正比例关系和反比例关系各一题,旨在熟练用比例解决问题的方法,及熟练解比例的方法。
环节三 拓展练习 1.一堆糖果,巧克力糖与糖果总块数的比是9:20。再放进32块椰子糖后,巧克力糖与糖果总块数的比是1:4。这堆糖果中有多少块巧克力糖? 练习:独立思考解题。 反馈。 2.王明在100 m赛跑中冲到终点时,领先刘铭10 m,领先李亮15 m,如果他们都按原来的速度,继续向前冲向终点,那么当刘铭到达终点时,李亮还差多少米到达终点? 引导:想一想什么不变? 练习:独立思考解题。 反馈。 小结:在解决稍复杂问题时,要先找到题目中不变的量,再根据不变的量找到比例关系。 方法一: 解:设这堆糖果中有9x块巧克力糖。 9x:(20x+32)=1:4 20x+32=36x 16x=32 x=2 巧克力糖:9x=18 答:这堆糖果中有18块巧克力糖。 方法二: 解:设这堆糖果中有x块巧克力糖。 x: (4x-32) = 9: 20 36x-288 = 20x 16x=288 x=18 答:这堆糖果中有18块巧克力糖。 三人在跑步过程中,因为速度保持不变,所以相同时间内的路程比一定。 解:设当刘铭到达终点时,李亮还差x米到达终点。 (100-10):(100-15)= 100: (100-x) 90:85=100:(100-x) 18:17=100:(100-x) 1800-18x=1700 18x=100 x=5 答:当刘铭到达终点时,李亮还差5米到达终点。 这两道拓展练习, 引导学生在复杂变化的情境中辨析寻找题目中能成比例的两种量, 提高学生灵活解决问题的能力。
环节四 课堂小结 你有什么收获? 生1:比例的意义 表示两个比相等的式子叫做比例。 比例的基本性质:a :b=c:d→a d=b c 生2:正比例关系 =k(一定) 反比例关系 xy=k(一定) 生3:比例的应用在解决问题时,要先找到题目中不变的量,再根据不变的量找到比例关系。 鼓励学生畅谈自己的收获和体会,有哪些认知上的冲突,遇到问题是如何解决的。
环节五 布置作业 教材 P66 第2、3、4题
1
单元综合复习
教学内容分析:
本课是人教版六年级下册第四单元的单元复习课。通过前几节课的学习学生已经知道了什么是比例、比例的基本性质、正比例和反比例及它们的应用等。本节课对这部分知识进行梳理,引导学生自主整理单元知识,体验归纳整理、构建知识体系的方法。针对各知识点适当的设计了有层次的习题,习题紧扣生活,在解决生活中的实际问题中培养灵活解决问题的能力,并感受数学在生活中的应用价值。
教学目标:
1.回顾比例的有关知识,能用比例解决生活中的实际问题。
2.经历比和比例知识的整理过程,沟通知识间的联系,体验对比、归纳等方法,培养合作意识,增强学生学好数学的信心。
3.能运用比和比例的知识解决简单的实际问题,丰富解决问题的策略,积累解决问题的经验。
教学重点:
对比和比例的知识进行系统整理。
教学难点:
理清知识间的联系,构建知识网络。
教学过程:
教学环节 教师活动 学生活动 设计意图
环节一 知识梳理 1.回顾比例的意义、比例的基本性质、正比例和反比例及其应用 引入:同学们,如果我们留意观察,就可以发现生活中处处有数学。比如:每天早上,老师都会骑自行车去学校上班,下面表格表示老师行驶的路程和时间的关系。 提问:你能在图中找到哪些比例? 追问:什么是比例? 追问:关于比例你还知道什么? 比较:比和比例有什么区别? 提问:从这张表中你还知道些什么? 提问:老师7:20出发,7:40到达学校,老师家离学校有多远? 追问: 老师家到学校的路程一定,行驶的速度和时间又成什么比例,为什么? 2.回顾比例的应用、图形的放大与缩小 提问:这是老师按1:80的比例在校园拍摄的一张照片,如果老师照片上的身高是2厘米,那么你能算出老师的实际身高吗? 提问:其实校门口还有一位同学,能看清他的样子吗? 追问:那怎么办? 出示:按7:1放大。 生:500 : 2 = 1000 : 4 1500 : 6 = 2000 : 8 1000 :1500 = 4 : 6 500 : 1000 = 2: 4…… 生:表示两个比相等的式子叫做比例。 生1:我知道组成比例的四个数叫做比例的项,两端的两项叫做比例的外项,中间的两项叫做比例的内项。 生2:我还知道两个外项的积等于两个内项的积,这是比例的基本性质。 生1:比是两个数相除,是式子;比例是两个相等的比组成的等式。 生2:比有两项,比例有四项。 生3:比有基本性质,它是化简比的依据;比例有基本性质,它是解比例的依据。 生:我发现行驶路程和时间的比值一定,所以行驶路程和时间成正比例关系,行驶路程和时间是成正比例的量。 生1:用算术法解决,根据“路程=速度×时间”,250×20=5000(米); 生2:可以用正比例解决问题, 设老师家到学校有x米, 500 : 2= x : 20 x =5000 答:老师家离学校5000米。 生:速度和时间成反比例关系,因为:速度×时间=路程(一定)。 生1:根据“图上距离:实际距离=1:80”,可以用解比例的方法解决问题。 解:设老师实际身高是x cm。 2:x=1:80 x=160 答:老师的实际身高是160 cm。 生2:根据“图上距离:实际距离=1:80”,推出“实际距离=图上距离÷ 2÷=160(cm) 答:老师实际身高是160 cm。 生:看不清。 生:按比例放大就能看清了。 通过创设现实情境,引导回顾比例意义、比例的基本性质、正比例和反比例及解决问题,在情境中自然用到这些知识来解决问题,提高学生复习的兴趣和效率。 将情境进行串联,由骑车到校切换到到达学校,并自然衔接到比例尺的复习及图形的放大与缩小,使知识整理更加有趣。
环节二 综合练习 1.填一填。 如果=y,那么x与y成( )比例;如果=y,那么x与y成( )比例。 在比例尺是6:1的平面图上量得零件的长为15 cm,零件的实际长是( )。 一个长6 cm,宽4 cm的长方形按1:2缩小,得到的图形的面积是( )cm 。 独立思考后反馈:你是怎么想的? 2.辨一辨。 下面各题中的两种量是否成比例关系?如果成比例关系,成什么比例关系? 长方体的高一定,体积和底面积。 圆的面积和它的半径。 长方形的周长一定,长和宽。 独立思考后反馈:你是怎么想的? 3.解决问题 (1)如图,长方形ABCD中,动点P沿着AB从A点运动到B点,三角形PAD的面积随着P点运动在不断地变化。 当PA=2 cm时,三角形PAD的面积是3 cm2,当PA=4.5 cm时, 三角形PAD的面积是多少平方厘米?(用比例解) 练习:独立思考解题。 反馈:你是怎么做的? (2)要给客厅铺地砖,如果用边长是6 dm的方砖,需要 80块;如果改用边长是8 dm的方砖,需要多少块?(用比例解) 练习:独立思考解题。 反馈:你是怎么做的? 小结:用比例解决问题,要先判断两个量成什么比例关系,再根据关系解决问题。 学生独立思考。 根据=y,可知=8,x与y成正比例; 根据=y,可知xy=8,x与y成反比例。 图上距离:实际距离=比例尺 解:设零件的实际长是x cm。 15:x=6:1 6x=15 x=2.5 (3)方法一: 缩小后长方形的长:6÷2=3(cm) 缩小后长方形的宽:4÷2=2(cm) 得到的图形的面积:3×2=6(cm ) 方法二: 原长方形面积:6×4=24(cm ) 缩小后的面积:24÷(2×2)=6(cm ) 成正比例,因为=高(一定)。 不成比例关系,=πr,比值不定。 (3)不成比例关系,长+宽=周长的一半(一定),长和宽的和一定,不成比例。 根据“三角形PAD∶PA=2×AD(一定)”可知三角形PAD的面积和PA成正比例关系。 解:设当PA=4.5 cm时,三角形PAD的面积是x cm 。 x∶4.5 = 3∶2 2x=13.5 x=6.75 答:设当PA=4.5 cm时,三角形PAD的面积是6.75 cm 。 根据“每块方砖面积×方砖数量=客厅面积(一定),可知每块方砖面积和方砖数量成反比例关系。 解:设需要x块。 8×8×x=6×6×80 8x=360 x=45 答:改用边长是8 dm的方砖,需要45块。 填一填是关于比例相关知识的基础练习,旨在熟练掌握。 辨一辨是判断两种量是否成比例关系,第2和第3题是典型错误,学生容易根据图形计算公式直接判断成比例关系,这两题意图从本质上理解如何判断两个量是否成比例关系。 这两道题要求用比例解决问题,正比例关系和反比例关系各一题,旨在熟练用比例解决问题的方法,及熟练解比例的方法。
环节三 拓展练习 1.一堆糖果,巧克力糖与糖果总块数的比是9:20。再放进32块椰子糖后,巧克力糖与糖果总块数的比是1:4。这堆糖果中有多少块巧克力糖? 练习:独立思考解题。 反馈。 2.王明在100 m赛跑中冲到终点时,领先刘铭10 m,领先李亮15 m,如果他们都按原来的速度,继续向前冲向终点,那么当刘铭到达终点时,李亮还差多少米到达终点? 引导:想一想什么不变? 练习:独立思考解题。 反馈。 小结:在解决稍复杂问题时,要先找到题目中不变的量,再根据不变的量找到比例关系。 方法一: 解:设这堆糖果中有9x块巧克力糖。 9x:(20x+32)=1:4 20x+32=36x 16x=32 x=2 巧克力糖:9x=18 答:这堆糖果中有18块巧克力糖。 方法二: 解:设这堆糖果中有x块巧克力糖。 x: (4x-32) = 9: 20 36x-288 = 20x 16x=288 x=18 答:这堆糖果中有18块巧克力糖。 三人在跑步过程中,因为速度保持不变,所以相同时间内的路程比一定。 解:设当刘铭到达终点时,李亮还差x米到达终点。 (100-10):(100-15)= 100: (100-x) 90:85=100:(100-x) 18:17=100:(100-x) 1800-18x=1700 18x=100 x=5 答:当刘铭到达终点时,李亮还差5米到达终点。 这两道拓展练习, 引导学生在复杂变化的情境中辨析寻找题目中能成比例的两种量, 提高学生灵活解决问题的能力。
环节四 课堂小结 你有什么收获? 生1:比例的意义 表示两个比相等的式子叫做比例。 比例的基本性质:a :b=c:d→a d=b c 生2:正比例关系 =k(一定) 反比例关系 xy=k(一定) 生3:比例的应用在解决问题时,要先找到题目中不变的量,再根据不变的量找到比例关系。 鼓励学生畅谈自己的收获和体会,有哪些认知上的冲突,遇到问题是如何解决的。
环节五 布置作业 教材 P66 第2、3、4题
1
