【解析版】新疆兵团第二师华山中学2013-2014学年高二下学期第一次月考数学(文)试题
文档属性
| 名称 | 【解析版】新疆兵团第二师华山中学2013-2014学年高二下学期第一次月考数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 615.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-29 04:07:32 | ||
图片预览



文档简介
2013-2014年第二学期高二年级第一次月考
数学 文科 试卷
(考试时间:120分钟,满分:150分) 命题教师:张庆磊
一、单选题(每小题5分,共12小题,共60分)
1.若命题“”为假,且“”为假,则( )
A.或为假 B.假 C.真 D.不能判断的真假
【答案】B
【解析】若命题“”为假,则p,q至少一个为假,若“”为假,则p为真,所以q为假。
2.命题:“x∈R,”的否定是( )
A.x∈R, B.x∈R,
C.x∈R, D.x∈R,
【答案】C
【解析】命题:“x∈R,”的否定是x∈R,。
3.已知,那么复数在平面内对应的点位于( )
A.第一象限 B. 第二象限 C.第三象限 D.第四象限
【答案】A
【解析】因为,所以,所以复数在平面内对应的点位于第一象限。
4.设则的关系是( )
A. B. C. D.无法确定
【答案】C
【解析】,,所以。
5.已知条件,条件,则是的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】A
【解析】由得,所以为;由得,所以为,所以是的充分不必要条件。
6.已知函数,则 ( )
A. B. 0 C. D.
【答案】A
【解析】因为函数,所以,所以。
7.某产品的广告费用x与销售额y的统计数据如下表
广告费用x(万元)
4
2
3
5
销售额y(万元)
49
26
39
54
根据上表可得回归方程中的为9.4,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元 B.65.5万元 C.67.7万元 D.72.0万元
【答案】B
【解析】易知:,又因为数据的样本中心点在线性回归直线上,所以代入回归直线方程得,所以,所以当x=6时,,即据此模型预报广告费用为6万元时销售额为65.5万元。
8.设则( )
A.都不大于 B.都不小于
C.至少有一个不大于 D.至少有一个不小于
【答案】C
【解析】假设三项都大于-2,则,由基本不等式得,所以,此与假设矛盾,所以至少有一个不大于。
9.若抛物线上一点到准线的距离等于它到顶点的距离,则点的坐标为( )
A. B. C. D.
【答案】B
【解析】因为点到准线的距离等于它到顶点的距离,由抛物线的定义知:点到焦点的距离等于它到顶点的距离,所以点P的横坐标为,代入得,所以点的坐标为。
10.函数的最大值为( )
A. B. C. D.
【答案】A
【解析】易知函数的定义域为,又,由;由,所以函数在单调递增,在单调递减,所以函数在x=e时取最大值,最大值为。
11.从椭圆上一点向轴作垂线,垂足恰为左焦点,是椭圆与轴正半轴的交点,是椭圆与轴正半轴的交点,且(是坐标原点),则该椭圆的离心率是( )
A. B. C. D.
【答案】C
【解析】因为,所以,所以该椭圆的离心率是。
12.已知函数有两个极值点,则实数的取值范围是( )
A. B. C. D.
【答案】B
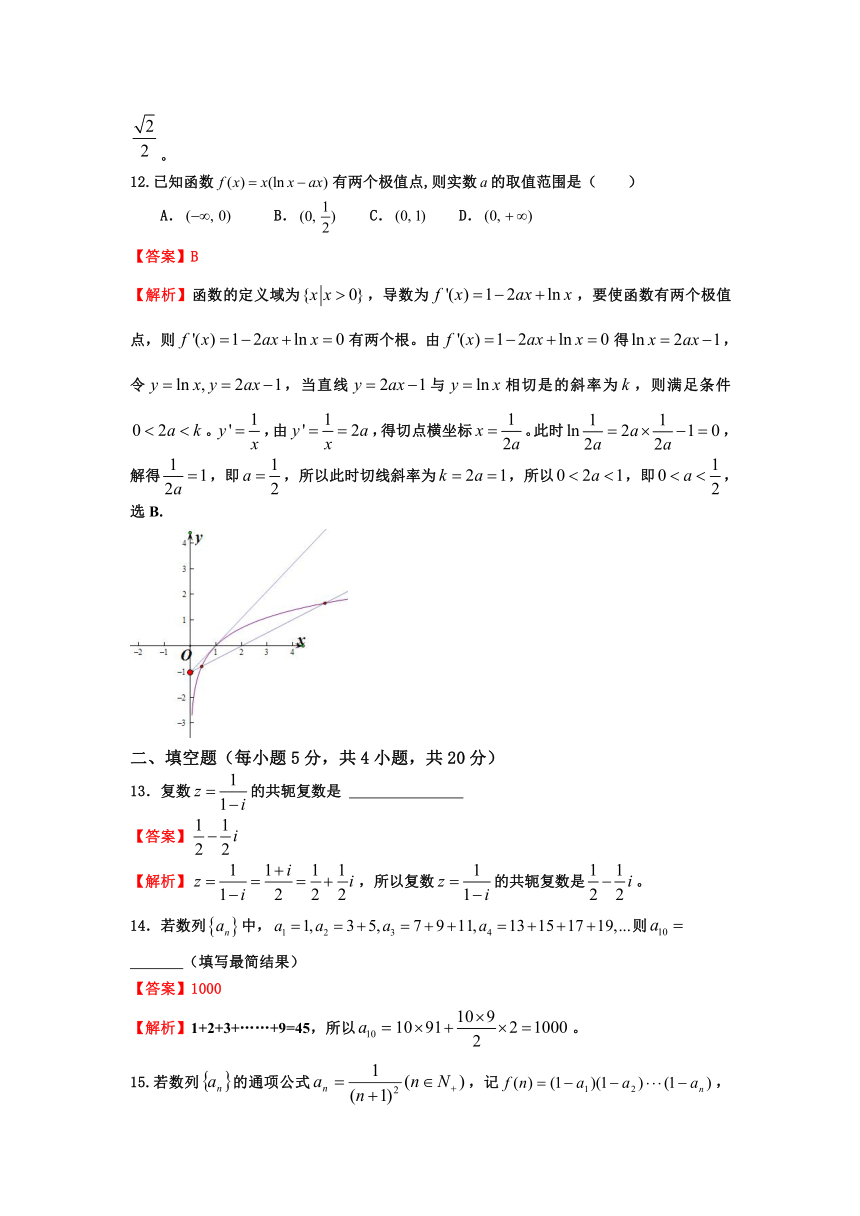
【解析】函数的定义域为,导数为,要使函数有两个极值点,则有两个根。由得,令,当直线与相切是的斜率为,则满足条件。,由,得切点横坐标。此时,解得,即,所以此时切线斜率为,所以,即,选B.
二、填空题(每小题5分,共4小题,共20分)
13.复数的共轭复数是
【答案】
【解析】,所以复数的共轭复数是。
14.若数列中,则
(填写最简结果)
【答案】1000
【解析】1+2+3+……+9=45,所以。
15.若数列的通项公式,记,试通过计算的值,推测出
【答案】
【解析】,,,……
推测出。
16.已知为双曲线的左焦点,为上的点,若的长等于虚轴长的2倍,点 在线段上,则的周长为 .
【答案】44
【解析】由图易知:,又,所以,所以的周长。
三、解答题(17题10分,18、19、20、21、22题各12分)
17.已知命题,命题,若是的充分不必要条件,求的取值范围。
18.从某居民区随机抽取10个家庭,获得第个家庭的月收入(单位:千元)与月储蓄(单位:千元)的数据资料,算得:,,,.
(Ⅰ)求家庭的月储蓄对月收入的线性回归方程;
(Ⅱ)若该居民区某家庭月收入为8000元,预测该家庭的月储蓄.
附:线性回归方程中,,,其中,为样本平均值.
19.某工科院校对A,B两个专业的男女生人数进行调查,得到如下的列联表:
?
专业A
专业B
总计
女生
12
4
16
男生
38
46
84
总计
50
50
100
(1)从B专业的女生中随机抽取2名女生参加某项活动,其中女生甲被选到的概率是多少?
(2)能否在犯错误的概率不超过0.05的前提下,认为工科院校中“性别”与“专业”有关系呢? 注:.
P(K2≥k0)
0.25
0.15
0.10
0.05
0.025
k0
1.323
2.072
2.706
3.841
5.024
20.(1)已知,求证:.
(2)已知 求证:
21.已知函数(其中均为常数,).当时,函数的极植为.
(1)试确定的值;
(2)求的单调区间;
(3)若对于任意,不等式恒成立,求的取值范围.
22.已知椭圆的一个顶点为A(0,-1),焦点在x轴上.若右焦点到直线的距离为3.
(1)求椭圆的方程;
(2)设椭圆与直线相交于不同的两点M、N.当时,求的取值范围.
数学 文科 试卷
(考试时间:120分钟,满分:150分) 命题教师:张庆磊
一、单选题(每小题5分,共12小题,共60分)
1.若命题“”为假,且“”为假,则( )
A.或为假 B.假 C.真 D.不能判断的真假
【答案】B
【解析】若命题“”为假,则p,q至少一个为假,若“”为假,则p为真,所以q为假。
2.命题:“x∈R,”的否定是( )
A.x∈R, B.x∈R,
C.x∈R, D.x∈R,
【答案】C
【解析】命题:“x∈R,”的否定是x∈R,。
3.已知,那么复数在平面内对应的点位于( )
A.第一象限 B. 第二象限 C.第三象限 D.第四象限
【答案】A
【解析】因为,所以,所以复数在平面内对应的点位于第一象限。
4.设则的关系是( )
A. B. C. D.无法确定
【答案】C
【解析】,,所以。
5.已知条件,条件,则是的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】A
【解析】由得,所以为;由得,所以为,所以是的充分不必要条件。
6.已知函数,则 ( )
A. B. 0 C. D.
【答案】A
【解析】因为函数,所以,所以。
7.某产品的广告费用x与销售额y的统计数据如下表
广告费用x(万元)
4
2
3
5
销售额y(万元)
49
26
39
54
根据上表可得回归方程中的为9.4,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元 B.65.5万元 C.67.7万元 D.72.0万元
【答案】B
【解析】易知:,又因为数据的样本中心点在线性回归直线上,所以代入回归直线方程得,所以,所以当x=6时,,即据此模型预报广告费用为6万元时销售额为65.5万元。
8.设则( )
A.都不大于 B.都不小于
C.至少有一个不大于 D.至少有一个不小于
【答案】C
【解析】假设三项都大于-2,则,由基本不等式得,所以,此与假设矛盾,所以至少有一个不大于。
9.若抛物线上一点到准线的距离等于它到顶点的距离,则点的坐标为( )
A. B. C. D.
【答案】B
【解析】因为点到准线的距离等于它到顶点的距离,由抛物线的定义知:点到焦点的距离等于它到顶点的距离,所以点P的横坐标为,代入得,所以点的坐标为。
10.函数的最大值为( )
A. B. C. D.
【答案】A
【解析】易知函数的定义域为,又,由;由,所以函数在单调递增,在单调递减,所以函数在x=e时取最大值,最大值为。
11.从椭圆上一点向轴作垂线,垂足恰为左焦点,是椭圆与轴正半轴的交点,是椭圆与轴正半轴的交点,且(是坐标原点),则该椭圆的离心率是( )
A. B. C. D.
【答案】C
【解析】因为,所以,所以该椭圆的离心率是。
12.已知函数有两个极值点,则实数的取值范围是( )
A. B. C. D.
【答案】B
【解析】函数的定义域为,导数为,要使函数有两个极值点,则有两个根。由得,令,当直线与相切是的斜率为,则满足条件。,由,得切点横坐标。此时,解得,即,所以此时切线斜率为,所以,即,选B.
二、填空题(每小题5分,共4小题,共20分)
13.复数的共轭复数是
【答案】
【解析】,所以复数的共轭复数是。
14.若数列中,则
(填写最简结果)
【答案】1000
【解析】1+2+3+……+9=45,所以。
15.若数列的通项公式,记,试通过计算的值,推测出
【答案】
【解析】,,,……
推测出。
16.已知为双曲线的左焦点,为上的点,若的长等于虚轴长的2倍,点 在线段上,则的周长为 .
【答案】44
【解析】由图易知:,又,所以,所以的周长。
三、解答题(17题10分,18、19、20、21、22题各12分)
17.已知命题,命题,若是的充分不必要条件,求的取值范围。
18.从某居民区随机抽取10个家庭,获得第个家庭的月收入(单位:千元)与月储蓄(单位:千元)的数据资料,算得:,,,.
(Ⅰ)求家庭的月储蓄对月收入的线性回归方程;
(Ⅱ)若该居民区某家庭月收入为8000元,预测该家庭的月储蓄.
附:线性回归方程中,,,其中,为样本平均值.
19.某工科院校对A,B两个专业的男女生人数进行调查,得到如下的列联表:
?
专业A
专业B
总计
女生
12
4
16
男生
38
46
84
总计
50
50
100
(1)从B专业的女生中随机抽取2名女生参加某项活动,其中女生甲被选到的概率是多少?
(2)能否在犯错误的概率不超过0.05的前提下,认为工科院校中“性别”与“专业”有关系呢? 注:.
P(K2≥k0)
0.25
0.15
0.10
0.05
0.025
k0
1.323
2.072
2.706
3.841
5.024
20.(1)已知,求证:.
(2)已知 求证:
21.已知函数(其中均为常数,).当时,函数的极植为.
(1)试确定的值;
(2)求的单调区间;
(3)若对于任意,不等式恒成立,求的取值范围.
22.已知椭圆的一个顶点为A(0,-1),焦点在x轴上.若右焦点到直线的距离为3.
(1)求椭圆的方程;
(2)设椭圆与直线相交于不同的两点M、N.当时,求的取值范围.
同课章节目录
