8.2 整式乘法(5) 课件(共25张PPT)
文档属性
| 名称 | 8.2 整式乘法(5) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
沪科版七年级下册
8.2整式乘法(5)
教学目标
1.认识多项式与多项式的乘法.
教学重点:
利用多项式与多项式乘法法则进行计算.
教学难点
能利用多项式与多项式的乘法法则进行计算.
2.能利用多项式与多项式乘法法则进行计算.
复习旧知
1.如何进行单项式与多项式乘法的运算?
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
2.计算
(1) (-8a2b) · (-3a)
(2) -3x2y3 · (x2-1)
+(x2 + 1)
· 3x2y3
=24a3b
=-3x4y3+3x2y3
+ 3x4y3+3x2y3
=6x2y3
新知导入
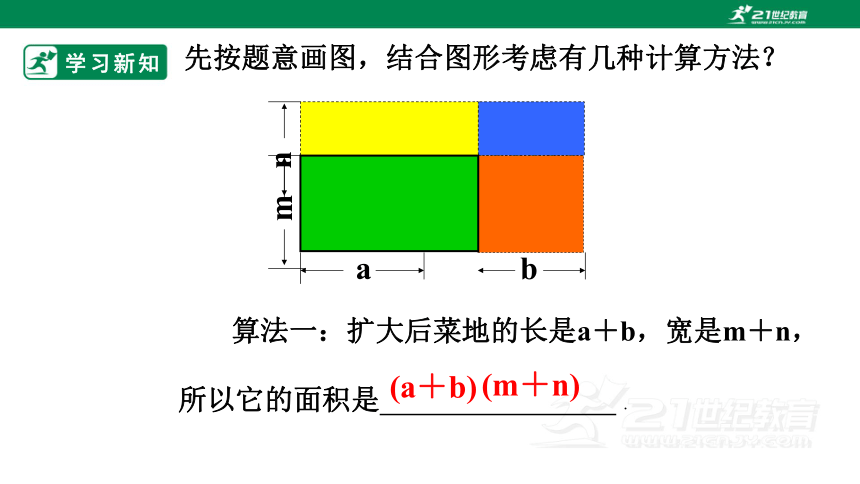
一块长方形的菜地,长为a,宽为m.
现将它的长增加b,宽增加n,求扩大后的
菜地的面积.
学习新知
所以它的面积是 .
先按题意画图,结合图形考虑有几种计算方法?
b
n
m
a
算法一:扩大后菜地的长是a+b,宽是m+n,
(a+b)
(m+n)
学习新知
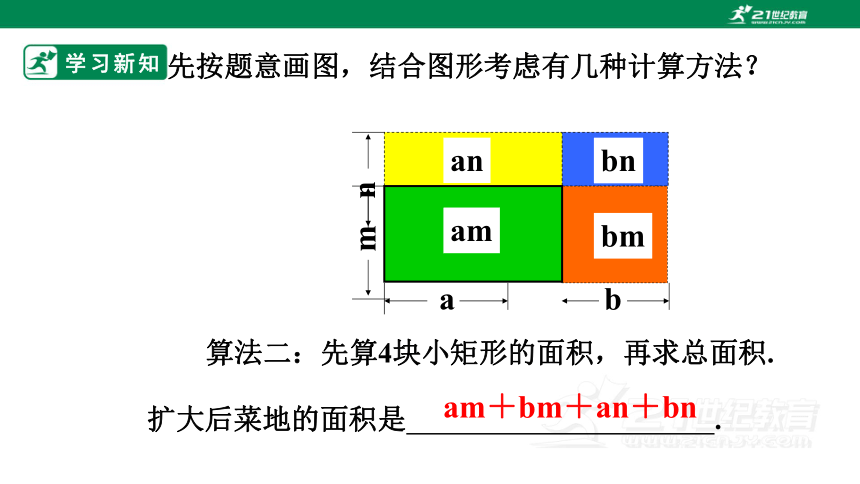
先按题意画图,结合图形考虑有几种计算方法?
b
n
m
a
am
bn
an
bm
算法二:先算4块小矩形的面积,再求总面积.
am+bm+an+bn
扩大后菜地的面积是 .
学习新知
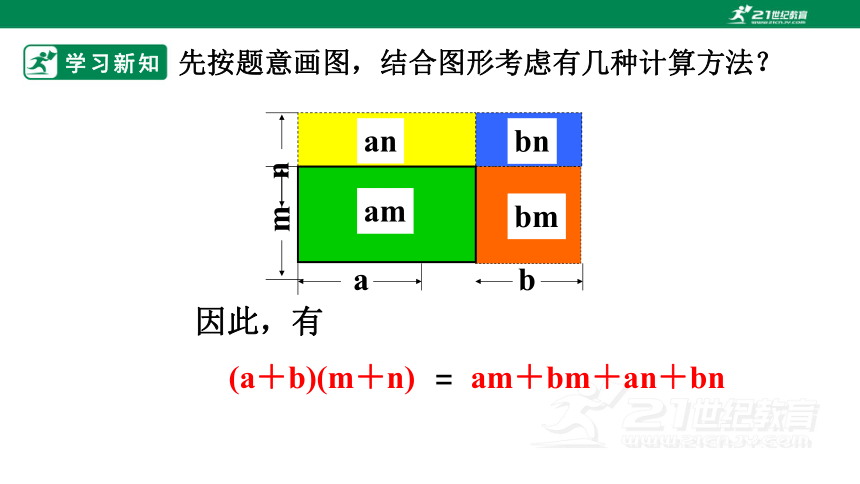
先按题意画图,结合图形考虑有几种计算方法?
b
n
m
a
am
bn
an
bm
am+bm+an+bn
(a+b)(m+n)
=
因此,有
学以致用
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)(m+n)
am
+an
+bm
+bn
am+bm+an+bn
(a+b)(m+n)
=
=
多项式与多项式相乘
学习新知
(a+b) (m+n) =
=
am+bm
+
an+bn
上面的运算还可以把(a+b)看作一个整体运用分配律,再根据单项式与多项式的相乘法则,得
(a+b) (m+n) =
am
+ an
+ bm
+ bn
(a+b) m
+ (a+b) n
am+bm+an+bn
(a+b)(m+n)
=
例题解析
例6 计算:
(2) (ax+b)(cx+d) .
(1) (-2x-1) (3x-2);
解:
=
=
=
-2x·
3x
3x
×
+
+
+
-6x2
+4x
-3x
+2
-6x2+x+2
(1) (-2x-1)(3x-2)
(-2x)·
(-2)
(-1) ·
(-1)
(-2)
例题解析
例6 计算:
(2) (ax+b)(cx+d) .
(1) (-2x-1) (3x-2);
解:
=
=
+
+
acx2
+
(ad+bc)x
+
bd
(2) (ax+b)(cx+d)
ax·
cx
+ax ·
d
b·
cx
bd
例题解析
(1) (a+b)(a2-ab+b2)
a3
-a2b
+ab2
+a2b
-ab2
+b3
=
=
a3
+b3
(1) (a+b)(a2-ab+b2);
例7 计算:
(2) (y2+y+1) (y+2).
解:
y3
+2y2
+y2
+2y
=
=
y3
+3y2
(2) (y2+y+1)(y+2)
+y+2
+3y+2
课堂练习
1. 计算:
(1) (2n+6) (n-3);
(2) (3x-y) (3x+y).
=2n2-6n
+6n-18
=2n2-18
=9x2+3xy
-3xy-y2
=9x2-y2
课堂练习
2. 计算:
(1) (3a-2)(a-1)+
(2) (3a+2)(3a-2)-
(a+1)(a+2)
9a(a-1)
=3a2-3a
-2a+2
+ a2+2a
+a+2
=4a2-2a+4
=9a2-6a
+6a-4
- 9a2+9a
=9a-4
课堂练习
(1) (x-y)(x2+xy+y2);
3.计算:
(2) (x+1) (x2-2x+3)
=x3+x2y+xy2
-x2 y-xy2-y3
=x3 -y3
=x3-2x2+3x
+x2-2x+3
=x3-x2+x +3
例题解析
解方程:(x-3)(x-2)=(x+9)(x+1)+12.
去括号,得
x2-2x-3x+6
=x2+ x+9x+9
+12
移项,合并同类项,得
-15x=15
解:
x=-1
系数化为1,得
学以致用
解方程:3x(x-2)+(x+1)(x - 1)=4(x2 +8).
去括号,得
3x2-2x
+ x2 -x+x - 1
移项,合并同类项,得
-3x=33
解:
x=-11
系数化为1,得
=4x2 +32
课堂小结
(1)本节课学习了哪些主要内容?
(2)在运用多项式与多项式相乘的法则时,你认为
应该注意哪些问题?
(3)举例说明在探索多项式与多项式相乘的法则的
过程中,体现了哪些思想方法?
课堂小结
多项式与多项式乘法法则是什么 如何推导
答:多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每相乘,再把所得的积相加.
对于(a+b)(m+n),把(a+b)看作一个整体,利用分配律,再根据单项式与多项式乘法法则,得:
(a+b)(m+n)=(a+b)m+(a+b)n
=am+bm+an+bn.
练习巩固
1.计算结果为 x2-5x-6的项是 ( ).
A.(x-1)(x+6) B.(x+1)(x-6)
C.(x-2)(x+3) D.(x+2)(x-3)
2.李老师做了一个长方形教具,其中一边长为
2a+b,另一边长为a-b,则该长方形的
面积为 ( ).
A.6a+b B.2a2-ab-b2
C.3a D.10a-b
B
B
练习巩固
3.计算:(a+2)(3-a)= .
4.商店经营一种产品,定价为12元/件,每天能售出
8件,而每降1元,则每天可多售(x+2)件,则降价
x元后,每天的销售总收入为 元.
-a2+a+6
(-x2+2x+120)
练习巩固
5.先化简,再求值:
(a-2b)(a2+2ab+4b )-a(a-5b)(a+3b),
其 a=- 1,b=1.
解:
原式=
当a= - 1,b=1时,
原式=2×(-1)2×1+15×(- 1)×12-8×13
a3+2a2b+4ab
-2a2b-4ab2-8b3
-a(a2-2ab-15b2)
=a3-8b3
-a3+2a2b+15ab2
=2a2b+15ab2-8b3
=-21.
作业布置
今天作业
课本P65页第4题
课本P66页第10、12题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版七年级下册
8.2整式乘法(5)
教学目标
1.认识多项式与多项式的乘法.
教学重点:
利用多项式与多项式乘法法则进行计算.
教学难点
能利用多项式与多项式的乘法法则进行计算.
2.能利用多项式与多项式乘法法则进行计算.
复习旧知
1.如何进行单项式与多项式乘法的运算?
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
2.计算
(1) (-8a2b) · (-3a)
(2) -3x2y3 · (x2-1)
+(x2 + 1)
· 3x2y3
=24a3b
=-3x4y3+3x2y3
+ 3x4y3+3x2y3
=6x2y3
新知导入
一块长方形的菜地,长为a,宽为m.
现将它的长增加b,宽增加n,求扩大后的
菜地的面积.
学习新知
所以它的面积是 .
先按题意画图,结合图形考虑有几种计算方法?
b
n
m
a
算法一:扩大后菜地的长是a+b,宽是m+n,
(a+b)
(m+n)
学习新知
先按题意画图,结合图形考虑有几种计算方法?
b
n
m
a
am
bn
an
bm
算法二:先算4块小矩形的面积,再求总面积.
am+bm+an+bn
扩大后菜地的面积是 .
学习新知
先按题意画图,结合图形考虑有几种计算方法?
b
n
m
a
am
bn
an
bm
am+bm+an+bn
(a+b)(m+n)
=
因此,有
学以致用
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)(m+n)
am
+an
+bm
+bn
am+bm+an+bn
(a+b)(m+n)
=
=
多项式与多项式相乘
学习新知
(a+b) (m+n) =
=
am+bm
+
an+bn
上面的运算还可以把(a+b)看作一个整体运用分配律,再根据单项式与多项式的相乘法则,得
(a+b) (m+n) =
am
+ an
+ bm
+ bn
(a+b) m
+ (a+b) n
am+bm+an+bn
(a+b)(m+n)
=
例题解析
例6 计算:
(2) (ax+b)(cx+d) .
(1) (-2x-1) (3x-2);
解:
=
=
=
-2x·
3x
3x
×
+
+
+
-6x2
+4x
-3x
+2
-6x2+x+2
(1) (-2x-1)(3x-2)
(-2x)·
(-2)
(-1) ·
(-1)
(-2)
例题解析
例6 计算:
(2) (ax+b)(cx+d) .
(1) (-2x-1) (3x-2);
解:
=
=
+
+
acx2
+
(ad+bc)x
+
bd
(2) (ax+b)(cx+d)
ax·
cx
+ax ·
d
b·
cx
bd
例题解析
(1) (a+b)(a2-ab+b2)
a3
-a2b
+ab2
+a2b
-ab2
+b3
=
=
a3
+b3
(1) (a+b)(a2-ab+b2);
例7 计算:
(2) (y2+y+1) (y+2).
解:
y3
+2y2
+y2
+2y
=
=
y3
+3y2
(2) (y2+y+1)(y+2)
+y+2
+3y+2
课堂练习
1. 计算:
(1) (2n+6) (n-3);
(2) (3x-y) (3x+y).
=2n2-6n
+6n-18
=2n2-18
=9x2+3xy
-3xy-y2
=9x2-y2
课堂练习
2. 计算:
(1) (3a-2)(a-1)+
(2) (3a+2)(3a-2)-
(a+1)(a+2)
9a(a-1)
=3a2-3a
-2a+2
+ a2+2a
+a+2
=4a2-2a+4
=9a2-6a
+6a-4
- 9a2+9a
=9a-4
课堂练习
(1) (x-y)(x2+xy+y2);
3.计算:
(2) (x+1) (x2-2x+3)
=x3+x2y+xy2
-x2 y-xy2-y3
=x3 -y3
=x3-2x2+3x
+x2-2x+3
=x3-x2+x +3
例题解析
解方程:(x-3)(x-2)=(x+9)(x+1)+12.
去括号,得
x2-2x-3x+6
=x2+ x+9x+9
+12
移项,合并同类项,得
-15x=15
解:
x=-1
系数化为1,得
学以致用
解方程:3x(x-2)+(x+1)(x - 1)=4(x2 +8).
去括号,得
3x2-2x
+ x2 -x+x - 1
移项,合并同类项,得
-3x=33
解:
x=-11
系数化为1,得
=4x2 +32
课堂小结
(1)本节课学习了哪些主要内容?
(2)在运用多项式与多项式相乘的法则时,你认为
应该注意哪些问题?
(3)举例说明在探索多项式与多项式相乘的法则的
过程中,体现了哪些思想方法?
课堂小结
多项式与多项式乘法法则是什么 如何推导
答:多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每相乘,再把所得的积相加.
对于(a+b)(m+n),把(a+b)看作一个整体,利用分配律,再根据单项式与多项式乘法法则,得:
(a+b)(m+n)=(a+b)m+(a+b)n
=am+bm+an+bn.
练习巩固
1.计算结果为 x2-5x-6的项是 ( ).
A.(x-1)(x+6) B.(x+1)(x-6)
C.(x-2)(x+3) D.(x+2)(x-3)
2.李老师做了一个长方形教具,其中一边长为
2a+b,另一边长为a-b,则该长方形的
面积为 ( ).
A.6a+b B.2a2-ab-b2
C.3a D.10a-b
B
B
练习巩固
3.计算:(a+2)(3-a)= .
4.商店经营一种产品,定价为12元/件,每天能售出
8件,而每降1元,则每天可多售(x+2)件,则降价
x元后,每天的销售总收入为 元.
-a2+a+6
(-x2+2x+120)
练习巩固
5.先化简,再求值:
(a-2b)(a2+2ab+4b )-a(a-5b)(a+3b),
其 a=- 1,b=1.
解:
原式=
当a= - 1,b=1时,
原式=2×(-1)2×1+15×(- 1)×12-8×13
a3+2a2b+4ab
-2a2b-4ab2-8b3
-a(a2-2ab-15b2)
=a3-8b3
-a3+2a2b+15ab2
=2a2b+15ab2-8b3
=-21.
作业布置
今天作业
课本P65页第4题
课本P66页第10、12题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
