专题23 “不动点法”处理迭代数列-2023年新高考数学重难点突破-(含答案)
文档属性
| 名称 | 专题23 “不动点法”处理迭代数列-2023年新高考数学重难点突破-(含答案) | 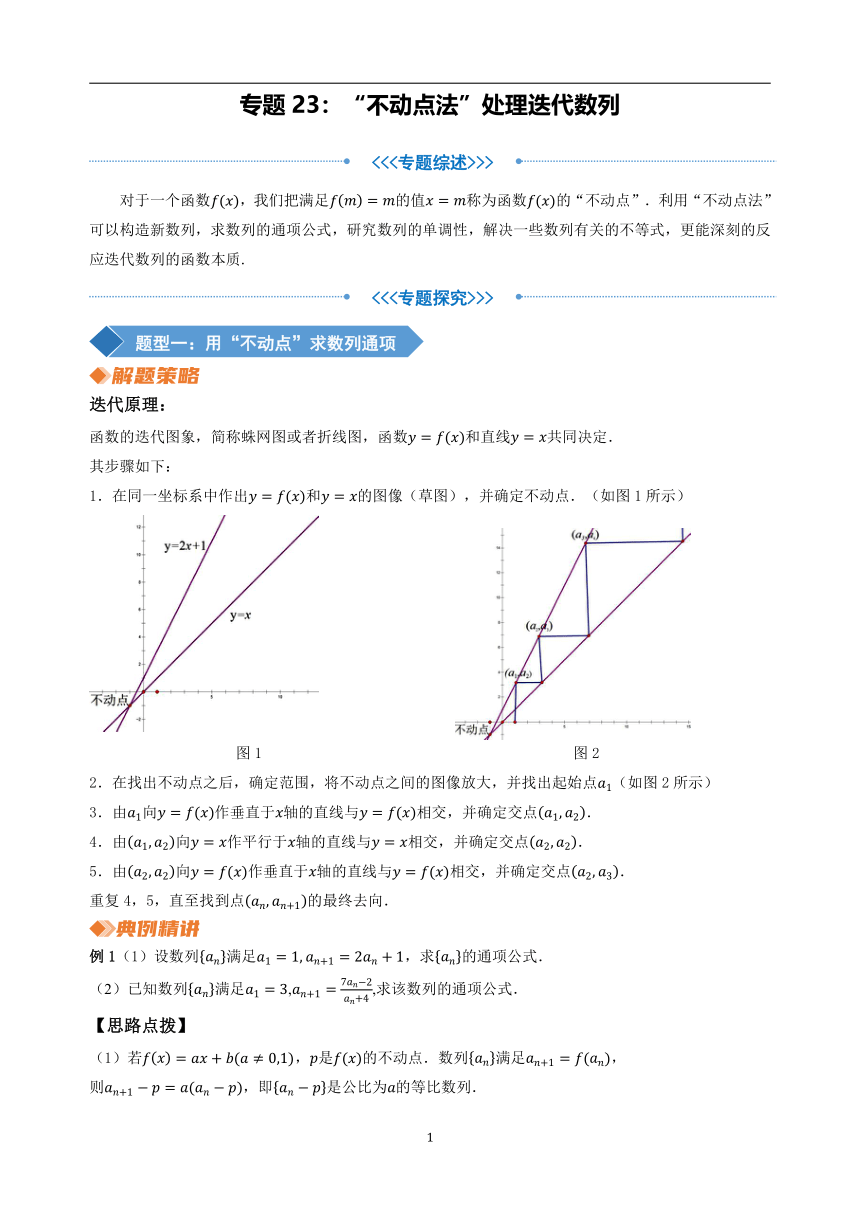 | |
| 格式 | docx | ||
| 文件大小 | 673.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-21 14:58:21 | ||
图片预览




文档简介
专题23:“不动点法”处理迭代数列
对于一个函数,我们把满足的值称为函数的“不动点”.利用“不动点法”可以构造新数列,求数列的通项公式,研究数列的单调性,解决一些数列有关的不等式,更能深刻的反应迭代数列的函数本质.
迭代原理:
函数的迭代图象,简称蛛网图或者折线图,函数和直线共同决定.
其步骤如下:
1.在同一坐标系中作出和的图像(草图),并确定不动点.(如图1所示)
图1 图2
2.在找出不动点之后,确定范围,将不动点之间的图像放大,并找出起始点(如图2所示)
3.由向作垂直于轴的直线与相交,并确定交点.
4.由向作平行于轴的直线与相交,并确定交点.
5.由向作垂直于轴的直线与相交,并确定交点.
重复4,5,直至找到点的最终去向.
例1(1)设数列满足,求的通项公式.
(2)已知数列满足,,求该数列的通项公式.
【思路点拨】
(1)若,是的不动点.数列满足,
则,即是公比为的等比数列.
(2)设 (),数列满足,.若有两个相异的不动点,则(此处.
练1已知数列满足,,求数列的通项公式.
练2设数列满足,且,
记,求数列的通项公式.
蛛网图与数列的单调性
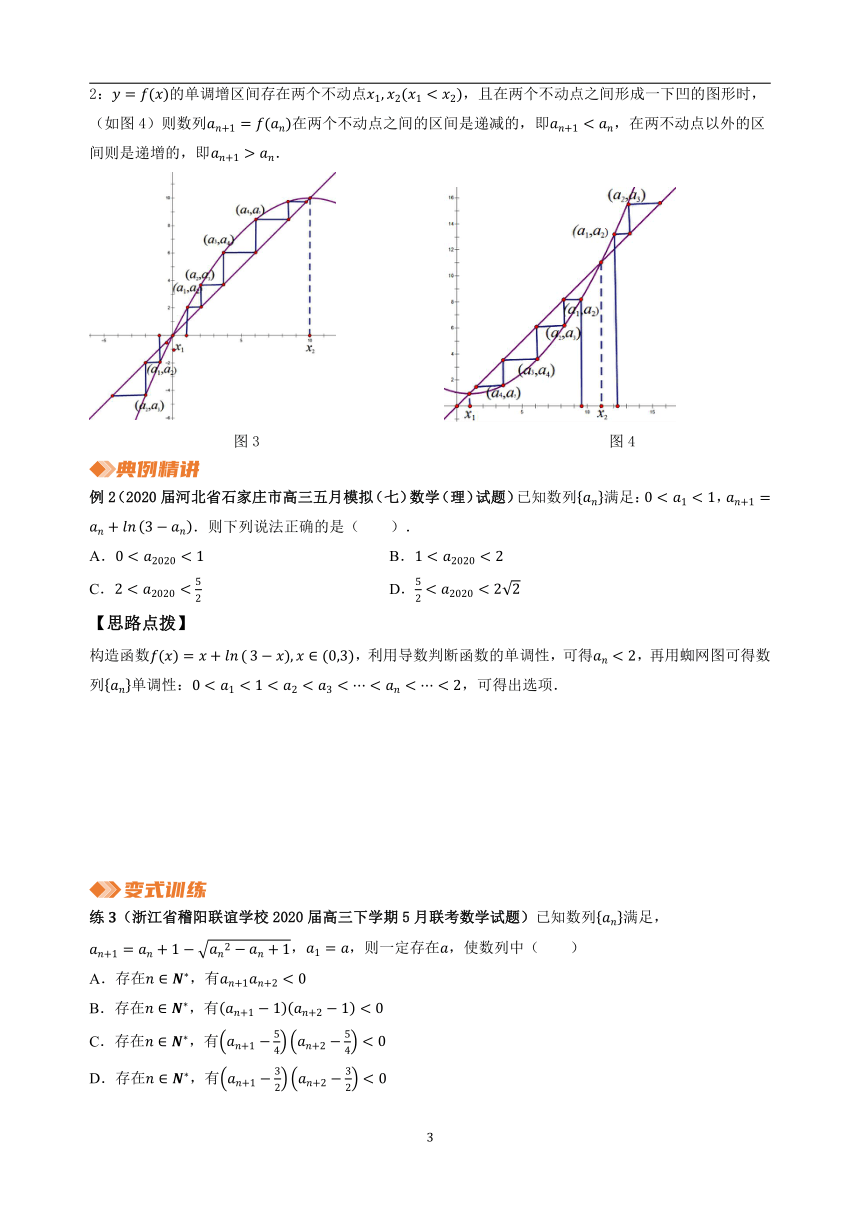
1:的单调增区间存在两个不动点,且在两个不动点之间形成一上凸的图形时,(如图3)则数列在两个不动点之间的区间是递增的,即,在两不动点以外的区间则是递减的,即.
2:的单调增区间存在两个不动点,且在两个不动点之间形成一下凹的图形时,(如图4)则数列在两个不动点之间的区间是递减的,即,在两不动点以外的区间则是递增的,即.
图3 图4
例2(2020届河北省石家庄市高三五月模拟(七)数学(理)试题)已知数列满足:,.则下列说法正确的是( ).
A. B.
C. D.
【思路点拨】
构造函数,利用导数判断函数的单调性,可得,再用蜘网图可得数列单调性:,可得出选项.
练3(浙江省稽阳联谊学校2020届高三下学期5月联考数学试题)已知数列满足,
,,则一定存在,使数列中( )
A.存在,有
B.存在,有
C.存在,有
D.存在,有
练4(浙江省杭州市第二中学滨江校区2021-2022学年高三上学期期中数学试题)已知数列满足(,为自然对数的底数),且对任意的都存在,使得成立,则数列的首项须满足( )
A. B. C. D.
1.已知数列满足,,求数列的通项公式.
2.已知数列满足,记数列的前项和为,则正确的是( )
A.存在,使得
B.存在,使得
C.存在,使得
D.存在,使得
3.已知无穷项数列,满足,且,下列关于数列描述正确的是( )
A.当且仅当时,数列单调递增
B.存在,使得数列为单调数列
C.当时,存在,使得
D.当时,数列一定存在无限多项的值大于
4.设数列满足, 证明:存在常数,使得对于任意的,都有
.
5.首项为正数的数列满足若对,一切都有,求的取值范围.
专题23 “不动点法”处理迭代数列
【专题探究】
例1【解析】(1)如上图1、图2可得,函数的不动点为-1,
故满足 即,
由数列构成的任一点均位于函数上,
故可知
∴是公比为的等比数列,
∴.
(2)由方程,得数列的不动点为和,
,
所以是首项为,公比为的等比数列,
所以,
解得,.
练1【解析】设,由,得.∴,
又,∴是以为首项,以为公比的等比数列,
∴,
∴,.
练2【解析】由已知得,由方程,得不动点.
所以,
又,
所以数列是首项为-2,公比为的等比数列,
所以,解得.
故.
例2【解析】令,
由可得在上单调递增,
由可得在单调递减,且,
可得,又恒成立,若,则数列为常数列,不满足,
所以,所以数列为单调递增数列,如图所示:
且,,
由图象可得,
所以,
故选:B.
练3【解析】因为,
所以在函数图象上,
因为与y=x有两个交点(0,0),(1,1),
如图所示:
可知当时,数列递减,∴0;
当时,数列递增,并且趋向1;
当时,数列递减,并且趋向,则可知错误;
又当时,,
则当时,一定小于,则之后均小于,∴D错误;
对于C,可取,得,,
所以,满足要求.
故选:C.
练4【解析】设,令,得到.
当时,,单调递减;
当时,,单调递增.
故,即(当且仅当时取等号).
故(当且仅当时取等号).
即.
要使对任意的都存在,使得成立,
显然时,,一定能满足题意;
当时,,如图此时不满足题意;
当时,,如图此时满足题意;
综上,.
故选:C.
【专题训练】
1. 【解析】解方程,
化简得,解得,
则,
又,
∴数列是以为首项,以为公比的等比数列,
∴,∴.
2. 【解析】设,则,
可知当时,单调递增,当时,单调递减,
令,
由于,
因此,在上有一零点,作出草图如图,利用蛛网法,
可知,故均为错误,选D.
故选:D.
3. 【解析】设函数,由,
可得函数在上单调递减,在上单调递增.
且当时,,则可以作出,如图.
且.
为无穷项数列,则.
选项A. 当时,由函数图像有,,
,所以此时数列单调递增,所以A不正确.
选项B. (1)当时,由函数图像可得,且,
由,根据上面对选项A的分析可知,数列从第2项起单调递增.
(2)当时,由函数图像可得,且,
,且,
根据上面对选项A的分析可知,数列从第3项起单调递增.
(3)当时,由函数图像可得.
如图,过点作轴的平行线交直线于点,
过点轴的垂线交于点,
过点作轴的平行线交直线于点,
过点轴的垂线交于点,
依此作下去,可得在开始阶段数列是递减的,如图,其值一定会递减至中.
若是第一个满足,可得,
由前面的证明可得,从数列从第项开始是递增的.
所以时,数列不是单调的,所以B不正确.
选项C.当时,由选项A的推导,可知数列单调递增,显然满足条件.
当时,由选项B的推导,可知数列第项开始是递增的,
显然满足条件. 所以C正确.
选项D. 由对选项B的判断过程可知,当时,数列先减后增,只有前面有限多项的值大于,递增部分的无限多项的值都小于,所以D错误.
故选:C
4. 【解析】令,当时,函数的不动点有,即或,两个不动点
(1)如图1所示,当时,通过蛛网图发现,
故,故当时,一定有;
(2)当时,总有,故当时,一定有;
(3)如图2所示,当时,通过蛛网图发现,
故只需,一定有;
综上,存在常数,使得对于任意的,都有.
5. 【解析】令,当时,函数的不动点有或,两个不动点(图3)
(1)如图4所示,当时,通过蛛网图发现,
故与题意要求不符合;
(2)如图5所示,当时,总有;
(3)如图6所示,当时,通过蛛网图发现,
综上,或者时,.
图3 图4
图5 图6
2
对于一个函数,我们把满足的值称为函数的“不动点”.利用“不动点法”可以构造新数列,求数列的通项公式,研究数列的单调性,解决一些数列有关的不等式,更能深刻的反应迭代数列的函数本质.
迭代原理:
函数的迭代图象,简称蛛网图或者折线图,函数和直线共同决定.
其步骤如下:
1.在同一坐标系中作出和的图像(草图),并确定不动点.(如图1所示)
图1 图2
2.在找出不动点之后,确定范围,将不动点之间的图像放大,并找出起始点(如图2所示)
3.由向作垂直于轴的直线与相交,并确定交点.
4.由向作平行于轴的直线与相交,并确定交点.
5.由向作垂直于轴的直线与相交,并确定交点.
重复4,5,直至找到点的最终去向.
例1(1)设数列满足,求的通项公式.
(2)已知数列满足,,求该数列的通项公式.
【思路点拨】
(1)若,是的不动点.数列满足,
则,即是公比为的等比数列.
(2)设 (),数列满足,.若有两个相异的不动点,则(此处.
练1已知数列满足,,求数列的通项公式.
练2设数列满足,且,
记,求数列的通项公式.
蛛网图与数列的单调性
1:的单调增区间存在两个不动点,且在两个不动点之间形成一上凸的图形时,(如图3)则数列在两个不动点之间的区间是递增的,即,在两不动点以外的区间则是递减的,即.
2:的单调增区间存在两个不动点,且在两个不动点之间形成一下凹的图形时,(如图4)则数列在两个不动点之间的区间是递减的,即,在两不动点以外的区间则是递增的,即.
图3 图4
例2(2020届河北省石家庄市高三五月模拟(七)数学(理)试题)已知数列满足:,.则下列说法正确的是( ).
A. B.
C. D.
【思路点拨】
构造函数,利用导数判断函数的单调性,可得,再用蜘网图可得数列单调性:,可得出选项.
练3(浙江省稽阳联谊学校2020届高三下学期5月联考数学试题)已知数列满足,
,,则一定存在,使数列中( )
A.存在,有
B.存在,有
C.存在,有
D.存在,有
练4(浙江省杭州市第二中学滨江校区2021-2022学年高三上学期期中数学试题)已知数列满足(,为自然对数的底数),且对任意的都存在,使得成立,则数列的首项须满足( )
A. B. C. D.
1.已知数列满足,,求数列的通项公式.
2.已知数列满足,记数列的前项和为,则正确的是( )
A.存在,使得
B.存在,使得
C.存在,使得
D.存在,使得
3.已知无穷项数列,满足,且,下列关于数列描述正确的是( )
A.当且仅当时,数列单调递增
B.存在,使得数列为单调数列
C.当时,存在,使得
D.当时,数列一定存在无限多项的值大于
4.设数列满足, 证明:存在常数,使得对于任意的,都有
.
5.首项为正数的数列满足若对,一切都有,求的取值范围.
专题23 “不动点法”处理迭代数列
【专题探究】
例1【解析】(1)如上图1、图2可得,函数的不动点为-1,
故满足 即,
由数列构成的任一点均位于函数上,
故可知
∴是公比为的等比数列,
∴.
(2)由方程,得数列的不动点为和,
,
所以是首项为,公比为的等比数列,
所以,
解得,.
练1【解析】设,由,得.∴,
又,∴是以为首项,以为公比的等比数列,
∴,
∴,.
练2【解析】由已知得,由方程,得不动点.
所以,
又,
所以数列是首项为-2,公比为的等比数列,
所以,解得.
故.
例2【解析】令,
由可得在上单调递增,
由可得在单调递减,且,
可得,又恒成立,若,则数列为常数列,不满足,
所以,所以数列为单调递增数列,如图所示:
且,,
由图象可得,
所以,
故选:B.
练3【解析】因为,
所以在函数图象上,
因为与y=x有两个交点(0,0),(1,1),
如图所示:
可知当时,数列递减,∴0;
当时,数列递增,并且趋向1;
当时,数列递减,并且趋向,则可知错误;
又当时,,
则当时,一定小于,则之后均小于,∴D错误;
对于C,可取,得,,
所以,满足要求.
故选:C.
练4【解析】设,令,得到.
当时,,单调递减;
当时,,单调递增.
故,即(当且仅当时取等号).
故(当且仅当时取等号).
即.
要使对任意的都存在,使得成立,
显然时,,一定能满足题意;
当时,,如图此时不满足题意;
当时,,如图此时满足题意;
综上,.
故选:C.
【专题训练】
1. 【解析】解方程,
化简得,解得,
则,
又,
∴数列是以为首项,以为公比的等比数列,
∴,∴.
2. 【解析】设,则,
可知当时,单调递增,当时,单调递减,
令,
由于,
因此,在上有一零点,作出草图如图,利用蛛网法,
可知,故均为错误,选D.
故选:D.
3. 【解析】设函数,由,
可得函数在上单调递减,在上单调递增.
且当时,,则可以作出,如图.
且.
为无穷项数列,则.
选项A. 当时,由函数图像有,,
,所以此时数列单调递增,所以A不正确.
选项B. (1)当时,由函数图像可得,且,
由,根据上面对选项A的分析可知,数列从第2项起单调递增.
(2)当时,由函数图像可得,且,
,且,
根据上面对选项A的分析可知,数列从第3项起单调递增.
(3)当时,由函数图像可得.
如图,过点作轴的平行线交直线于点,
过点轴的垂线交于点,
过点作轴的平行线交直线于点,
过点轴的垂线交于点,
依此作下去,可得在开始阶段数列是递减的,如图,其值一定会递减至中.
若是第一个满足,可得,
由前面的证明可得,从数列从第项开始是递增的.
所以时,数列不是单调的,所以B不正确.
选项C.当时,由选项A的推导,可知数列单调递增,显然满足条件.
当时,由选项B的推导,可知数列第项开始是递增的,
显然满足条件. 所以C正确.
选项D. 由对选项B的判断过程可知,当时,数列先减后增,只有前面有限多项的值大于,递增部分的无限多项的值都小于,所以D错误.
故选:C
4. 【解析】令,当时,函数的不动点有,即或,两个不动点
(1)如图1所示,当时,通过蛛网图发现,
故,故当时,一定有;
(2)当时,总有,故当时,一定有;
(3)如图2所示,当时,通过蛛网图发现,
故只需,一定有;
综上,存在常数,使得对于任意的,都有.
5. 【解析】令,当时,函数的不动点有或,两个不动点(图3)
(1)如图4所示,当时,通过蛛网图发现,
故与题意要求不符合;
(2)如图5所示,当时,总有;
(3)如图6所示,当时,通过蛛网图发现,
综上,或者时,.
图3 图4
图5 图6
2
同课章节目录
