第四单元_第10课时_ 用比例解决问题(2)(教学课件)-六年级数学下册人教版(共25张PPT)
文档属性
| 名称 | 第四单元_第10课时_ 用比例解决问题(2)(教学课件)-六年级数学下册人教版(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 20:41:32 | ||
图片预览







文档简介
(共25张PPT)
小学数学·六年级(下)·RJ
第10课时 用比例解决问题(2)
正确利用反比例知识列出方程,解决生活中简单的实际问题。
进一步理解反比例的意义,掌握用反比例知识解决问题的方法与步骤。
感受比例知识与生活的紧密联系,增强用数学的眼光看世界的意识,激发学习兴趣。
掌握用反比例知识解决问题的方法与步骤。
正确利用反比例知识列出方程,解决生活中简单的实际问题。
利用归总思想,提高学生分析问题,解决问题的能力。
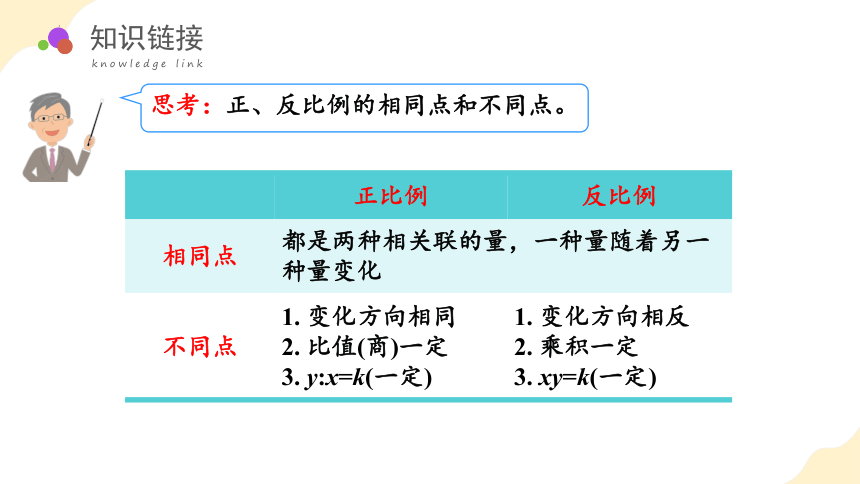
思考:正、反比例的相同点和不同点。
正比例 反比例
相同点 都是两种相关联的量,一种量随着另一种量变化 不同点 1. 变化方向相同 2. 比值(商)一定 3. y:x=k(一定) 1. 变化方向相反
2. 乘积一定
3. xy=k(一定)
判断下面各题中的两个量成什么比例。
(1)工作总量一定,工作效率和工作时间。
(2)总路程一定,已行的路程和剩下的路程。
(3)平行四边形的面积一定,平行四边形的底和对应的高。
不成比例
成反比例
成反比例
用算术方法解决问题
某办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
你能从题中获取哪些信息?
平均每天照明用电 用电天数
原来
现在
100千瓦时
5天
知道了:
?天
要解决的问题是:
原来5天的用电量现在可以用多少天?
25千瓦时
阅读与理解
某办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
可以怎样解答?
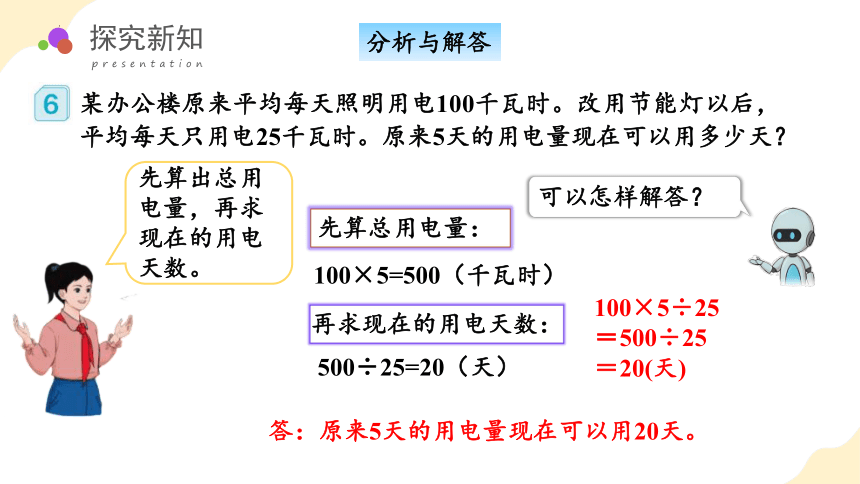
分析与解答
先算出总用电量,再求现在的用电天数。
先算总用电量:
100×5=500(千瓦时)
再求现在的用电天数:
答:原来5天的用电量现在可以用20天。
500÷25=20(天)
100×5÷25
=500÷25
=20(天)
某办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
还可以怎样思考?
分析与解答
还可以先算原来1天的电量可以供现在用几天,然后再算5天的。
100÷25=4(天)
答:原来5天的用电量现在可以用20天。
5×4=20(天)
100÷25×5
=4×5
=20(天)
用反比例知识解决问题
某办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
你能从题中获取哪些信息?
平均每天照明用电 用电天数
原来
现在
100千瓦时
5天
知道了:
?天
要解决的问题是:
原来5天的用电量现在可以用多少天?
25千瓦时
分析与解答
从题目中发现哪些量?
某办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
这些量成什么数量关系?
总用电量一定,每天用电量与用电天数成反比例。
分析与解答
解:设原来5天的用电量现在可以用x天。
25x = 100×5
x =
100×5
25
x = 20
答:原来5天的用电量现在可以用20天。
某办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
解决这个问题的关键是找到那两个量的乘积一定。
只要两个量的乘积一定,就可以用反比例关系解答。
某办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
回顾与反思
现在30天的用电量原来只够用多少天?
解:设现在30天的用电量原来只够用x天。
100x=25×30
x=7.5
答:现在30天的用电量原来只够用7.5天。
达标检测,巩固练习
1.小商店有两种圆珠笔。小明带的钱刚好可以买4支单价是1.5元的圆珠笔,如果他只买单价是2元的圆珠笔, 可以买多少支?
解:设如果他只买单价是2元的圆珠笔,可以买x支。
2x=4×1.5
答:如果他只买单价是2元的圆珠笔,可以买3支。
x=
4×1.5
2
x=3
2. 工程队修一条水渠,每天工作6小时,12天可以完成。如果每小时的工作量不变,每天工作8小时,多少天可以完成任务?
解:设x天可以完成任务。
8x=6×12
x=9
答:9天可以完成任务。
3.小林读一本文学名著,如果每天读30页,8天可以读完。小林想6天读完,那么平均每天要读多少页?
解:设平均每天要读x页。
6x=30×8
x=40
答:平均每天要读40页。
4.装修一个房间,用边长是4dm的方砖铺地,需要180块,用边长是3dm的方砖铺地,需要多少块
解:设需要x块。
4×4×180 = 3×3×x
x = 320
答:需要320块。
5.一堆煤,原计划每天烧3吨,可以烧72天。改进技术后,每天少烧0.6吨,这堆煤可以比原来多烧几天
解:设改进技术后可以烧x天。
3×72=(3 - 0.6) x
x =90
90-72=18
答:这堆煤可以比原来多烧18天。
6.用收割机收割小麦。如果每小时收割0.3公顷,40小时能完成任务。
(1)现在想用30小时收割完,那么每小时应收割多少公顷?
解:设每小时应收割x公顷。
30x = 0.3×40
x = 0.4
答:每小时应收割0.4公顷。
6.用收割机收割小麦。如果每小时收割0.3公顷,40小时能完成任务。
(2)每公顷产小麦8t,这块地一共产小麦多少吨?
(2)0.3×40×8=96(吨)
答:这块地一共产小麦96吨。
这节课你有什么收获?
用反比例解决问题的步骤:
1
2
分析这两种量所对应的两个数的比值是否一定,判断能否用比例解决。
设未知数,列反比例关系式。解方程,并写出答语。
小学数学·六年级(下)·RJ
第10课时 用比例解决问题(2)
正确利用反比例知识列出方程,解决生活中简单的实际问题。
进一步理解反比例的意义,掌握用反比例知识解决问题的方法与步骤。
感受比例知识与生活的紧密联系,增强用数学的眼光看世界的意识,激发学习兴趣。
掌握用反比例知识解决问题的方法与步骤。
正确利用反比例知识列出方程,解决生活中简单的实际问题。
利用归总思想,提高学生分析问题,解决问题的能力。
思考:正、反比例的相同点和不同点。
正比例 反比例
相同点 都是两种相关联的量,一种量随着另一种量变化 不同点 1. 变化方向相同 2. 比值(商)一定 3. y:x=k(一定) 1. 变化方向相反
2. 乘积一定
3. xy=k(一定)
判断下面各题中的两个量成什么比例。
(1)工作总量一定,工作效率和工作时间。
(2)总路程一定,已行的路程和剩下的路程。
(3)平行四边形的面积一定,平行四边形的底和对应的高。
不成比例
成反比例
成反比例
用算术方法解决问题
某办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
你能从题中获取哪些信息?
平均每天照明用电 用电天数
原来
现在
100千瓦时
5天
知道了:
?天
要解决的问题是:
原来5天的用电量现在可以用多少天?
25千瓦时
阅读与理解
某办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
可以怎样解答?
分析与解答
先算出总用电量,再求现在的用电天数。
先算总用电量:
100×5=500(千瓦时)
再求现在的用电天数:
答:原来5天的用电量现在可以用20天。
500÷25=20(天)
100×5÷25
=500÷25
=20(天)
某办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
还可以怎样思考?
分析与解答
还可以先算原来1天的电量可以供现在用几天,然后再算5天的。
100÷25=4(天)
答:原来5天的用电量现在可以用20天。
5×4=20(天)
100÷25×5
=4×5
=20(天)
用反比例知识解决问题
某办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
你能从题中获取哪些信息?
平均每天照明用电 用电天数
原来
现在
100千瓦时
5天
知道了:
?天
要解决的问题是:
原来5天的用电量现在可以用多少天?
25千瓦时
分析与解答
从题目中发现哪些量?
某办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
这些量成什么数量关系?
总用电量一定,每天用电量与用电天数成反比例。
分析与解答
解:设原来5天的用电量现在可以用x天。
25x = 100×5
x =
100×5
25
x = 20
答:原来5天的用电量现在可以用20天。
某办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
解决这个问题的关键是找到那两个量的乘积一定。
只要两个量的乘积一定,就可以用反比例关系解答。
某办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
回顾与反思
现在30天的用电量原来只够用多少天?
解:设现在30天的用电量原来只够用x天。
100x=25×30
x=7.5
答:现在30天的用电量原来只够用7.5天。
达标检测,巩固练习
1.小商店有两种圆珠笔。小明带的钱刚好可以买4支单价是1.5元的圆珠笔,如果他只买单价是2元的圆珠笔, 可以买多少支?
解:设如果他只买单价是2元的圆珠笔,可以买x支。
2x=4×1.5
答:如果他只买单价是2元的圆珠笔,可以买3支。
x=
4×1.5
2
x=3
2. 工程队修一条水渠,每天工作6小时,12天可以完成。如果每小时的工作量不变,每天工作8小时,多少天可以完成任务?
解:设x天可以完成任务。
8x=6×12
x=9
答:9天可以完成任务。
3.小林读一本文学名著,如果每天读30页,8天可以读完。小林想6天读完,那么平均每天要读多少页?
解:设平均每天要读x页。
6x=30×8
x=40
答:平均每天要读40页。
4.装修一个房间,用边长是4dm的方砖铺地,需要180块,用边长是3dm的方砖铺地,需要多少块
解:设需要x块。
4×4×180 = 3×3×x
x = 320
答:需要320块。
5.一堆煤,原计划每天烧3吨,可以烧72天。改进技术后,每天少烧0.6吨,这堆煤可以比原来多烧几天
解:设改进技术后可以烧x天。
3×72=(3 - 0.6) x
x =90
90-72=18
答:这堆煤可以比原来多烧18天。
6.用收割机收割小麦。如果每小时收割0.3公顷,40小时能完成任务。
(1)现在想用30小时收割完,那么每小时应收割多少公顷?
解:设每小时应收割x公顷。
30x = 0.3×40
x = 0.4
答:每小时应收割0.4公顷。
6.用收割机收割小麦。如果每小时收割0.3公顷,40小时能完成任务。
(2)每公顷产小麦8t,这块地一共产小麦多少吨?
(2)0.3×40×8=96(吨)
答:这块地一共产小麦96吨。
这节课你有什么收获?
用反比例解决问题的步骤:
1
2
分析这两种量所对应的两个数的比值是否一定,判断能否用比例解决。
设未知数,列反比例关系式。解方程,并写出答语。
