2022-2023学年高二下学期物理人教版(2019版)选择性必修一 第二章 机械振动 单元检测(A卷)(含解析)
文档属性
| 名称 | 2022-2023学年高二下学期物理人教版(2019版)选择性必修一 第二章 机械振动 单元检测(A卷)(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 624.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-03-21 19:32:16 | ||
图片预览



文档简介
第二章 机械振动 单元检测(A卷)
一、单选题
1.—位游客在湖边欲乘游船,当日风浪很大,游船上下浮动.可把游艇浮动简化成竖直方向的简谐运动,振幅为20cm,周期为3.0s.当船上升到最高点时,甲板刚好与码头地面平齐.地面与甲板的高度差不超过10cm时,游客能舒服地登船.在一个周期内,游客能舒服地登船的时间是()
A.0.5s
B.0.75s
C.1.0s
D.2.0s
2.“单摆”是一种理想化模型,如图所示,为l轻绳下端拴着一个可视为质点的小球,上端固定放在倾角为的光滑斜面上,这个装置也可以等效为“单摆”,当摆球在斜面所在的平面内做小摆角振动时的周期为
A. B.
C. D.以上答案都不对
3.如图所示,在一根张紧的水平绳上挂有5个单摆,其中摆球质量最大,其余4个摆球质量相等,摆长关系为 ,现将摆垂直纸面向里拉开一微小角度后释放,经过一段时间后,其余各摆均振动起来并达到稳定时的情况是( )
A.4个单摆的周期
B.4个单摆的频率
C.4个单摆的振幅
D.4个单摆中摆的振幅最小,且
4.如图所示,甲质点在x1轴上做简谐运动,O1为其平衡位置,A1、B1为其所能达到的最远处。乙质点沿x2轴从A2点开始做初速度为零的匀加速直线运动。已知A1O1=A2O2,甲、乙两质点分别经过O1、O2时速率相等,设甲质点从A1运动到O1的时间为t1,乙质点从A2运动到O2的时间为t2,则( )
A.t1=t2 B.t1>t2
C.t15.对水平弹簧振子,下列说法正确的是( )
A.每次通过同一位置时,其速度不一定相同,但加速度一定相同
B.通过平衡位置时,速度为零,加速度最大
C.每次通过平衡位置时,加速度相同,速度也一定相同
D.若位移为负值,则速度一定为正值,加速度也一定为正值
6.一砝码和一轻弹簧构成弹簧振子,图甲所示的装置可用于研究该弹簧振子的受迫振动,匀速转动把手时,曲杆给弹簧振子以驱动力,使振子做受迫振动,把手匀速转动的周期就是驱动力的周期,改变把手匀速转动的速度就可以改变驱动力的周期。若保持把手不动,给砝码一向下的初速度,砝码便做简谐运动,振动图线如图乙所示。当把手以某一速度匀速转动受迫振动达到稳定时,砝码的振动图线如图丙所示。若用表示弹簧振子的固有周期,表示驱动力的周期,表示受迫振动达到稳定后砝码振动的振幅,则( )
A.由图线可知s,振幅为8cm
B.由图线可知s,振幅为2cm
C.当T在4s附近时,Y显著增大;当T比4s小得多或大得多时,Y很小
D.当T在8s附近时,Y显著增大;当T比8s小得多或大得多时,Y很小
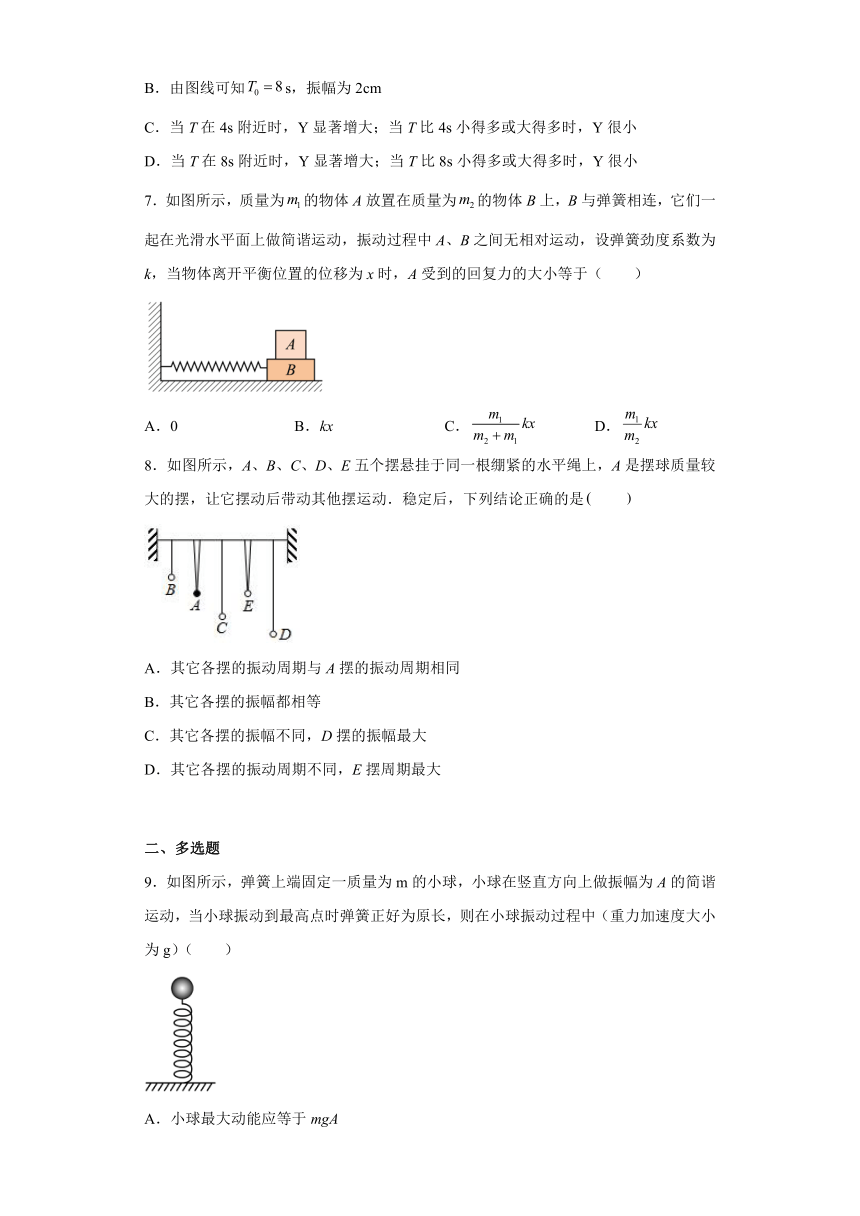
7.如图所示,质量为的物体A放置在质量为的物体B上,B与弹簧相连,它们一起在光滑水平面上做简谐运动,振动过程中A、B之间无相对运动,设弹簧劲度系数为k,当物体离开平衡位置的位移为x时,A受到的回复力的大小等于( )
A.0 B.kx C. D.
8.如图所示,A、B、C、D、E五个摆悬挂于同一根绷紧的水平绳上,A是摆球质量较大的摆,让它摆动后带动其他摆运动.稳定后,下列结论正确的是
A.其它各摆的振动周期与A摆的振动周期相同
B.其它各摆的振幅都相等
C.其它各摆的振幅不同,D摆的振幅最大
D.其它各摆的振动周期不同,E摆周期最大
二、多选题
9.如图所示,弹簧上端固定一质量为m的小球,小球在竖直方向上做振幅为A的简谐运动,当小球振动到最高点时弹簧正好为原长,则在小球振动过程中(重力加速度大小为g)( )
A.小球最大动能应等于mgA
B.弹簧的弹性势能和小球动能总和保持不变
C.弹簧最大弹性势能等于2mgA
D.小球在最低点时受到的弹力等于2mg
10.一简谐振子沿轴振动,平衡位置在坐标原点,时振子的位移为m,s时振子位移第一次为m,s时振子位移第二次为m,该振子的周期可能为( )
A.s B.8s C.s D.16s
11.2020年7月23日,我国首次发射火星探测器“天问一号”。地面上周期为2s的单摆经常被称为秒摆。假如某秒摆被“天问一号”探测器携带至火星表面后,周期变为3s,已知火星半径约为地球半径的二分之一,以下说法正确的是( )
A.若秒摆在火星表面的摆角变小,则周期也会随之变小
B.地球质量约为火星质量的9倍
C.火星的第一宇宙速度约为地球第一宇宙速度的倍
D.“天问一号”探测器刚发射离开地球表面时,此秒摆的周期大于2s
12.如图所示是甲、乙两个单摆做简谐运动的图像,则下列说法中正确的是
A.甲、乙两摆的振幅之比为2∶1
B.时,甲摆的重力势能最小,乙摆的动能为零
C.甲、乙两球的摆长之比为4∶1
D.甲、乙两摆摆球在最低点时向心加速度大小一定相等
三、实验题
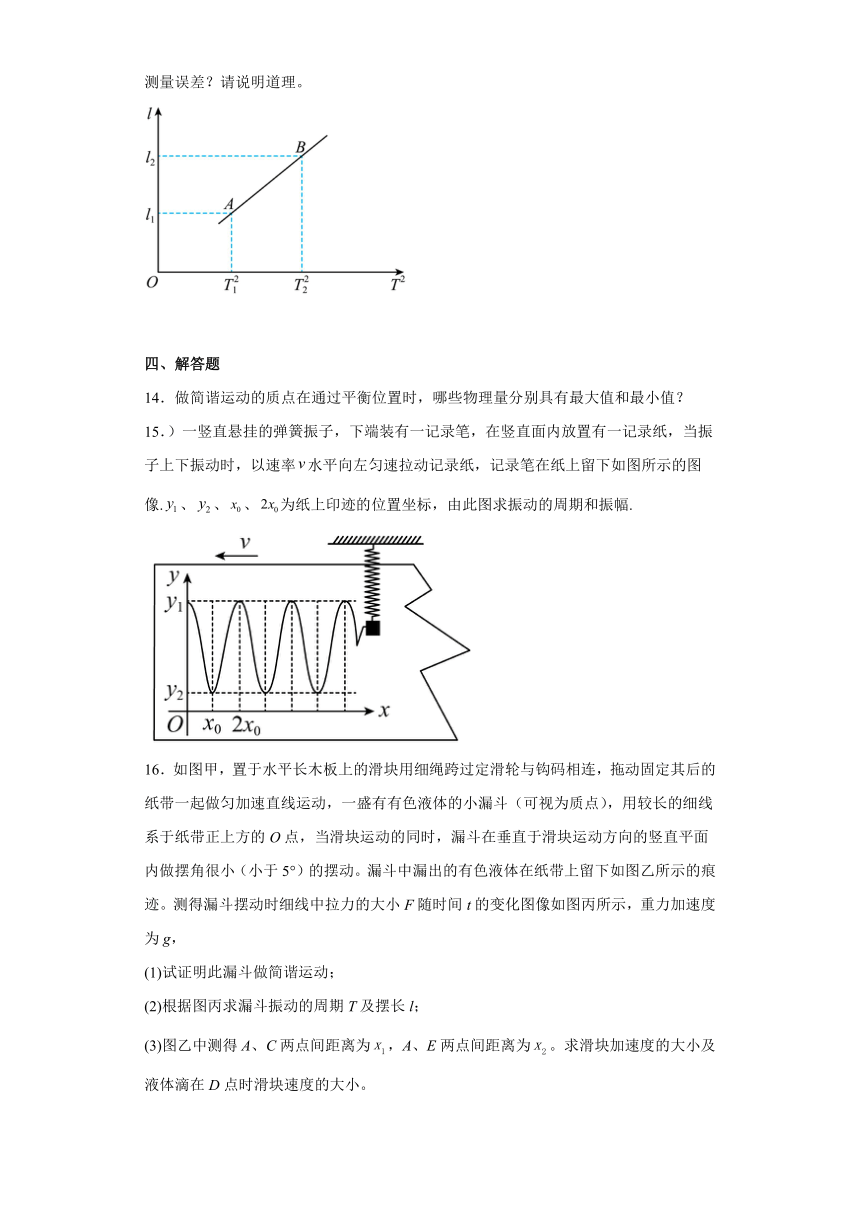
13.某同学用单摆测重力加速度。实验时改变摆长,测出几组摆长和对应的周期的数据,作出图像,如图所示。
(1)利用、两点的坐标可求得重力加速度,请写出重力加速度的表达式。
(2)本实验用图像计算重力加速度,是否可以消除因摆球质量分布不均匀而造成的测量误差?请说明道理。
四、解答题
14.做简谐运动的质点在通过平衡位置时,哪些物理量分别具有最大值和最小值?
15.)一竖直悬挂的弹簧振子,下端装有一记录笔,在竖直面内放置有一记录纸,当振子上下振动时,以速率水平向左匀速拉动记录纸,记录笔在纸上留下如图所示的图像.、、、为纸上印迹的位置坐标,由此图求振动的周期和振幅.
16.如图甲,置于水平长木板上的滑块用细绳跨过定滑轮与钩码相连,拖动固定其后的纸带一起做匀加速直线运动,一盛有有色液体的小漏斗(可视为质点),用较长的细线系于纸带正上方的O点,当滑块运动的同时,漏斗在垂直于滑块运动方向的竖直平面内做摆角很小(小于5°)的摆动。漏斗中漏出的有色液体在纸带上留下如图乙所示的痕迹。测得漏斗摆动时细线中拉力的大小F随时间t的变化图像如图丙所示,重力加速度为g,
(1)试证明此漏斗做简谐运动;
(2)根据图丙求漏斗振动的周期T及摆长l;
(3)图乙中测得A、C两点间距离为,A、E两点间距离为。求滑块加速度的大小及液体滴在D点时滑块速度的大小。
参考答案:
1.C
【详解】把船浮动简化成竖直方向的简谐运动,从船上升到最高点时计时,其振动方程为:,代入得:cm,当时,可解得:,故在一个周期内,游客能舒服登船的时间是,故ABD错误,C正确
2.C
【详解】在斜面上,根据牛顿第二定律可知,沿斜面向下的加速度为,所以单摆的周期为,ABD错误C正确.
3.B
【详解】AB.b 摆垂直纸面向里拉开一微小角度后释放,使得其他4个单摆都做受迫振动,受迫振动的频率等于驱动力的频率,所以4个单摆频率相同,周期也一样,所以A错误,B正确;
CD.当驱动力的频率接近物体的固有频率时,振幅最大,即达到共振.根据知,d摆长与b摆长相等,则驱动力的周期等于d摆的固有周期,发生共振,所以d摆振幅最大,CD错误。
故选B。
4.C
【详解】已知A1O1=A2O2,甲、乙两质点分别经过O1、O2时速率相等,结合题意,作出甲质点从A1到O1与乙质点从A2到O2过程的v-t图像,如图所示
容易得出
t1故选C。
5.A
【详解】A.弹簧振子的运动具有重复性,经过任意位置(除最大位移处)速度有来回两个相反的方向,所以经过同一位置速度不一定相同,但加速度一定相同,故A正确;
B.振子每次通过平衡位置时,速度最大,加速度为零,故B错误;
C.振子每次通过平衡位置时,加速度为零,故相同;但速度有两个相反的方向,不一定相同,故C错误;
D.若位移为负值,则速度可正可负还可以为零,故D错误。
故选A。
6.C
【详解】AB.图象乙是物体自由振动时的周期,故由图象乙可知,物体的固有频率为
振幅为4cm,故A、B错误;
CD.当物体的驱动力的频率等于物体的固有频率时,物体的振动达到最强,故当在4s附近时,振幅显著增大,当比4s小很多或大得很多时,很小,故C正确,D错误;
故选C。
7.C
【详解】物体A和B为整体做简谐运动,当物体离开平衡位置的位移为时,回复力的大小即为弹簧的弹力大小为,则对整体为研究对象有
则整体的加速度
则对物体A为研究对象,使其产生加速度的力即为物体B对物体A的静摩擦力,因此由牛顿第二定律可知
ABD错误,C正确。
故选C。
8.A
【详解】A摆摆动,其余各摆也摆动起来,它们均做受迫振动,则它们的振动周期均等于A摆的摆动周期,而由于A、E摆长相同,这两个摆的固有周期相同,则E摆出现共振现象,振幅达到最大;故选A.
【点睛】本题关键明确两点:受迫振动的频率等于驱动力的频率;当受迫振动中的固有频率等于驱动力频率时,出现共振现象.
9.CD
【详解】A.小球在平衡位置时,有
在平衡位置时动能最大,有
mgA=Ek+Ep
故A错误;
B.因为运动过程中弹簧与小球组成的系统机械能守恒,因此动能、重力势能和弹性势能之和保持不变,故B错误;
CD.从最高点到最低点,重力势能全部转化为弹性势能
Epm=2mgA
最低点加速度大小等于最高点加速度大小,据牛顿第二定律可知
F-mg=mg
得
F=2mg
故CD正确。
故选CD。
10.AB
【详解】如果振幅等于0.1 m,则
即振子的周期为s;如果振幅大于0.1m,则周期
故选AB。
11.BC
【详解】A.根据单摆的摆动周期公式
可知周期与振幅无关,故A错误;
B.根据单摆的摆动周期公式
周期比为
联立可得
又
半径关系为
可得
故B正确;
C.根据万有引力提供向心力
可得第一宇宙速度
则火星的第一宇宙速度与地球第一宇宙速度之比为
故C正确;
D.“天问一号”刚发射离开地球表面时,秒摆处于超重状态,由
可知秒表的周期小于2s,故D错误。
故选BC。
12.AB
【详解】A.由图知甲、乙两摆的振幅分别为2cm、1cm,振幅之比为2:1,故选项A正确;
B.t=2s时,甲摆在平衡位置处,则甲单摆的重力势能为零;乙摆在振动的最大位移处,动能为零,故选项B正确;
C.由单摆的周期公式
得到甲、乙两摆的摆长之比为1:4,故选项C错误;
D.因摆球摆动的最大偏角未知,无法判断两单摆摆球在最低点时向心加速度大小关系,故选项D错误。
故选AB。
13.(1) ;(2) 可以消除.
【详解】(1)由周期公式
可得
由图像可知
代入数据可得
(2)通过第(1)问的结论可以知道,若摆球的质量分布不均匀,l-T2图像的斜率不变,可消除因摆球质量分布不均匀而造成的测量误差。
14.速度、动能具有最大值,位移、回复力、加速度和势能具有最小值。
【详解】做简谐运动的质点,当它通过平衡位置时位移为零,根据简谐运动中的回复力F=-kx,则知回复力等于0;由加速度与位移关系
则知加速度为0。质点通过平衡位置时速度最大,动能最大,势能最小。
15. ;
【详解】试题分析:设周期为,振幅为.
由题意可得:
16.(1)见解析;(2)2t0; (3) ;
【详解】(1)对漏斗,设当偏角为θ时,位移为x,且设位移x的方向为正方向.
重力垂直绳方向的分力提供回复力
F=mgsinθ
当θ很小时
回复力方向与x方向相反,可得
满足F=-kx,可知漏斗的振动为简谐振动。
(2)根据图丙求可知漏斗振动的周期
T=2t0
根据单摆的周期公式
可得摆长
(3)由匀变速直线运动的规律可知
即
解得
液滴在D点时滑块速度的大小
一、单选题
1.—位游客在湖边欲乘游船,当日风浪很大,游船上下浮动.可把游艇浮动简化成竖直方向的简谐运动,振幅为20cm,周期为3.0s.当船上升到最高点时,甲板刚好与码头地面平齐.地面与甲板的高度差不超过10cm时,游客能舒服地登船.在一个周期内,游客能舒服地登船的时间是()
A.0.5s
B.0.75s
C.1.0s
D.2.0s
2.“单摆”是一种理想化模型,如图所示,为l轻绳下端拴着一个可视为质点的小球,上端固定放在倾角为的光滑斜面上,这个装置也可以等效为“单摆”,当摆球在斜面所在的平面内做小摆角振动时的周期为
A. B.
C. D.以上答案都不对
3.如图所示,在一根张紧的水平绳上挂有5个单摆,其中摆球质量最大,其余4个摆球质量相等,摆长关系为 ,现将摆垂直纸面向里拉开一微小角度后释放,经过一段时间后,其余各摆均振动起来并达到稳定时的情况是( )
A.4个单摆的周期
B.4个单摆的频率
C.4个单摆的振幅
D.4个单摆中摆的振幅最小,且
4.如图所示,甲质点在x1轴上做简谐运动,O1为其平衡位置,A1、B1为其所能达到的最远处。乙质点沿x2轴从A2点开始做初速度为零的匀加速直线运动。已知A1O1=A2O2,甲、乙两质点分别经过O1、O2时速率相等,设甲质点从A1运动到O1的时间为t1,乙质点从A2运动到O2的时间为t2,则( )
A.t1=t2 B.t1>t2
C.t1
A.每次通过同一位置时,其速度不一定相同,但加速度一定相同
B.通过平衡位置时,速度为零,加速度最大
C.每次通过平衡位置时,加速度相同,速度也一定相同
D.若位移为负值,则速度一定为正值,加速度也一定为正值
6.一砝码和一轻弹簧构成弹簧振子,图甲所示的装置可用于研究该弹簧振子的受迫振动,匀速转动把手时,曲杆给弹簧振子以驱动力,使振子做受迫振动,把手匀速转动的周期就是驱动力的周期,改变把手匀速转动的速度就可以改变驱动力的周期。若保持把手不动,给砝码一向下的初速度,砝码便做简谐运动,振动图线如图乙所示。当把手以某一速度匀速转动受迫振动达到稳定时,砝码的振动图线如图丙所示。若用表示弹簧振子的固有周期,表示驱动力的周期,表示受迫振动达到稳定后砝码振动的振幅,则( )
A.由图线可知s,振幅为8cm
B.由图线可知s,振幅为2cm
C.当T在4s附近时,Y显著增大;当T比4s小得多或大得多时,Y很小
D.当T在8s附近时,Y显著增大;当T比8s小得多或大得多时,Y很小
7.如图所示,质量为的物体A放置在质量为的物体B上,B与弹簧相连,它们一起在光滑水平面上做简谐运动,振动过程中A、B之间无相对运动,设弹簧劲度系数为k,当物体离开平衡位置的位移为x时,A受到的回复力的大小等于( )
A.0 B.kx C. D.
8.如图所示,A、B、C、D、E五个摆悬挂于同一根绷紧的水平绳上,A是摆球质量较大的摆,让它摆动后带动其他摆运动.稳定后,下列结论正确的是
A.其它各摆的振动周期与A摆的振动周期相同
B.其它各摆的振幅都相等
C.其它各摆的振幅不同,D摆的振幅最大
D.其它各摆的振动周期不同,E摆周期最大
二、多选题
9.如图所示,弹簧上端固定一质量为m的小球,小球在竖直方向上做振幅为A的简谐运动,当小球振动到最高点时弹簧正好为原长,则在小球振动过程中(重力加速度大小为g)( )
A.小球最大动能应等于mgA
B.弹簧的弹性势能和小球动能总和保持不变
C.弹簧最大弹性势能等于2mgA
D.小球在最低点时受到的弹力等于2mg
10.一简谐振子沿轴振动,平衡位置在坐标原点,时振子的位移为m,s时振子位移第一次为m,s时振子位移第二次为m,该振子的周期可能为( )
A.s B.8s C.s D.16s
11.2020年7月23日,我国首次发射火星探测器“天问一号”。地面上周期为2s的单摆经常被称为秒摆。假如某秒摆被“天问一号”探测器携带至火星表面后,周期变为3s,已知火星半径约为地球半径的二分之一,以下说法正确的是( )
A.若秒摆在火星表面的摆角变小,则周期也会随之变小
B.地球质量约为火星质量的9倍
C.火星的第一宇宙速度约为地球第一宇宙速度的倍
D.“天问一号”探测器刚发射离开地球表面时,此秒摆的周期大于2s
12.如图所示是甲、乙两个单摆做简谐运动的图像,则下列说法中正确的是
A.甲、乙两摆的振幅之比为2∶1
B.时,甲摆的重力势能最小,乙摆的动能为零
C.甲、乙两球的摆长之比为4∶1
D.甲、乙两摆摆球在最低点时向心加速度大小一定相等
三、实验题
13.某同学用单摆测重力加速度。实验时改变摆长,测出几组摆长和对应的周期的数据,作出图像,如图所示。
(1)利用、两点的坐标可求得重力加速度,请写出重力加速度的表达式。
(2)本实验用图像计算重力加速度,是否可以消除因摆球质量分布不均匀而造成的测量误差?请说明道理。
四、解答题
14.做简谐运动的质点在通过平衡位置时,哪些物理量分别具有最大值和最小值?
15.)一竖直悬挂的弹簧振子,下端装有一记录笔,在竖直面内放置有一记录纸,当振子上下振动时,以速率水平向左匀速拉动记录纸,记录笔在纸上留下如图所示的图像.、、、为纸上印迹的位置坐标,由此图求振动的周期和振幅.
16.如图甲,置于水平长木板上的滑块用细绳跨过定滑轮与钩码相连,拖动固定其后的纸带一起做匀加速直线运动,一盛有有色液体的小漏斗(可视为质点),用较长的细线系于纸带正上方的O点,当滑块运动的同时,漏斗在垂直于滑块运动方向的竖直平面内做摆角很小(小于5°)的摆动。漏斗中漏出的有色液体在纸带上留下如图乙所示的痕迹。测得漏斗摆动时细线中拉力的大小F随时间t的变化图像如图丙所示,重力加速度为g,
(1)试证明此漏斗做简谐运动;
(2)根据图丙求漏斗振动的周期T及摆长l;
(3)图乙中测得A、C两点间距离为,A、E两点间距离为。求滑块加速度的大小及液体滴在D点时滑块速度的大小。
参考答案:
1.C
【详解】把船浮动简化成竖直方向的简谐运动,从船上升到最高点时计时,其振动方程为:,代入得:cm,当时,可解得:,故在一个周期内,游客能舒服登船的时间是,故ABD错误,C正确
2.C
【详解】在斜面上,根据牛顿第二定律可知,沿斜面向下的加速度为,所以单摆的周期为,ABD错误C正确.
3.B
【详解】AB.b 摆垂直纸面向里拉开一微小角度后释放,使得其他4个单摆都做受迫振动,受迫振动的频率等于驱动力的频率,所以4个单摆频率相同,周期也一样,所以A错误,B正确;
CD.当驱动力的频率接近物体的固有频率时,振幅最大,即达到共振.根据知,d摆长与b摆长相等,则驱动力的周期等于d摆的固有周期,发生共振,所以d摆振幅最大,CD错误。
故选B。
4.C
【详解】已知A1O1=A2O2,甲、乙两质点分别经过O1、O2时速率相等,结合题意,作出甲质点从A1到O1与乙质点从A2到O2过程的v-t图像,如图所示
容易得出
t1
5.A
【详解】A.弹簧振子的运动具有重复性,经过任意位置(除最大位移处)速度有来回两个相反的方向,所以经过同一位置速度不一定相同,但加速度一定相同,故A正确;
B.振子每次通过平衡位置时,速度最大,加速度为零,故B错误;
C.振子每次通过平衡位置时,加速度为零,故相同;但速度有两个相反的方向,不一定相同,故C错误;
D.若位移为负值,则速度可正可负还可以为零,故D错误。
故选A。
6.C
【详解】AB.图象乙是物体自由振动时的周期,故由图象乙可知,物体的固有频率为
振幅为4cm,故A、B错误;
CD.当物体的驱动力的频率等于物体的固有频率时,物体的振动达到最强,故当在4s附近时,振幅显著增大,当比4s小很多或大得很多时,很小,故C正确,D错误;
故选C。
7.C
【详解】物体A和B为整体做简谐运动,当物体离开平衡位置的位移为时,回复力的大小即为弹簧的弹力大小为,则对整体为研究对象有
则整体的加速度
则对物体A为研究对象,使其产生加速度的力即为物体B对物体A的静摩擦力,因此由牛顿第二定律可知
ABD错误,C正确。
故选C。
8.A
【详解】A摆摆动,其余各摆也摆动起来,它们均做受迫振动,则它们的振动周期均等于A摆的摆动周期,而由于A、E摆长相同,这两个摆的固有周期相同,则E摆出现共振现象,振幅达到最大;故选A.
【点睛】本题关键明确两点:受迫振动的频率等于驱动力的频率;当受迫振动中的固有频率等于驱动力频率时,出现共振现象.
9.CD
【详解】A.小球在平衡位置时,有
在平衡位置时动能最大,有
mgA=Ek+Ep
故A错误;
B.因为运动过程中弹簧与小球组成的系统机械能守恒,因此动能、重力势能和弹性势能之和保持不变,故B错误;
CD.从最高点到最低点,重力势能全部转化为弹性势能
Epm=2mgA
最低点加速度大小等于最高点加速度大小,据牛顿第二定律可知
F-mg=mg
得
F=2mg
故CD正确。
故选CD。
10.AB
【详解】如果振幅等于0.1 m,则
即振子的周期为s;如果振幅大于0.1m,则周期
故选AB。
11.BC
【详解】A.根据单摆的摆动周期公式
可知周期与振幅无关,故A错误;
B.根据单摆的摆动周期公式
周期比为
联立可得
又
半径关系为
可得
故B正确;
C.根据万有引力提供向心力
可得第一宇宙速度
则火星的第一宇宙速度与地球第一宇宙速度之比为
故C正确;
D.“天问一号”刚发射离开地球表面时,秒摆处于超重状态,由
可知秒表的周期小于2s,故D错误。
故选BC。
12.AB
【详解】A.由图知甲、乙两摆的振幅分别为2cm、1cm,振幅之比为2:1,故选项A正确;
B.t=2s时,甲摆在平衡位置处,则甲单摆的重力势能为零;乙摆在振动的最大位移处,动能为零,故选项B正确;
C.由单摆的周期公式
得到甲、乙两摆的摆长之比为1:4,故选项C错误;
D.因摆球摆动的最大偏角未知,无法判断两单摆摆球在最低点时向心加速度大小关系,故选项D错误。
故选AB。
13.(1) ;(2) 可以消除.
【详解】(1)由周期公式
可得
由图像可知
代入数据可得
(2)通过第(1)问的结论可以知道,若摆球的质量分布不均匀,l-T2图像的斜率不变,可消除因摆球质量分布不均匀而造成的测量误差。
14.速度、动能具有最大值,位移、回复力、加速度和势能具有最小值。
【详解】做简谐运动的质点,当它通过平衡位置时位移为零,根据简谐运动中的回复力F=-kx,则知回复力等于0;由加速度与位移关系
则知加速度为0。质点通过平衡位置时速度最大,动能最大,势能最小。
15. ;
【详解】试题分析:设周期为,振幅为.
由题意可得:
16.(1)见解析;(2)2t0; (3) ;
【详解】(1)对漏斗,设当偏角为θ时,位移为x,且设位移x的方向为正方向.
重力垂直绳方向的分力提供回复力
F=mgsinθ
当θ很小时
回复力方向与x方向相反,可得
满足F=-kx,可知漏斗的振动为简谐振动。
(2)根据图丙求可知漏斗振动的周期
T=2t0
根据单摆的周期公式
可得摆长
(3)由匀变速直线运动的规律可知
即
解得
液滴在D点时滑块速度的大小
