北师大版七年级数学下册 3.2 用关系式表示的变量间关系 同步教学课件(共20张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 3.2 用关系式表示的变量间关系 同步教学课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 15:25:37 | ||
图片预览




文档简介
(共20张PPT)
3.2 用关系式表示的变量
间关系
第三章 变量之间的关系
课程讲授
新知导入
随堂练习
课堂小结
知识要点
1.用关系式表示的变量间关系
2.根据关系式求值
新知导入
想一想:
在“小车下滑的时间”中,
1.支撑物的高度h和小车下滑的时间t都在变化,
它们都是变量.其中小车下滑的时间t随支撑物
的高度h的变化而变化;
2.支撑物的高度h是自变量;
3.小车下滑的时间t是因变量.
课程讲授
1
用关系式表示的变量间关系
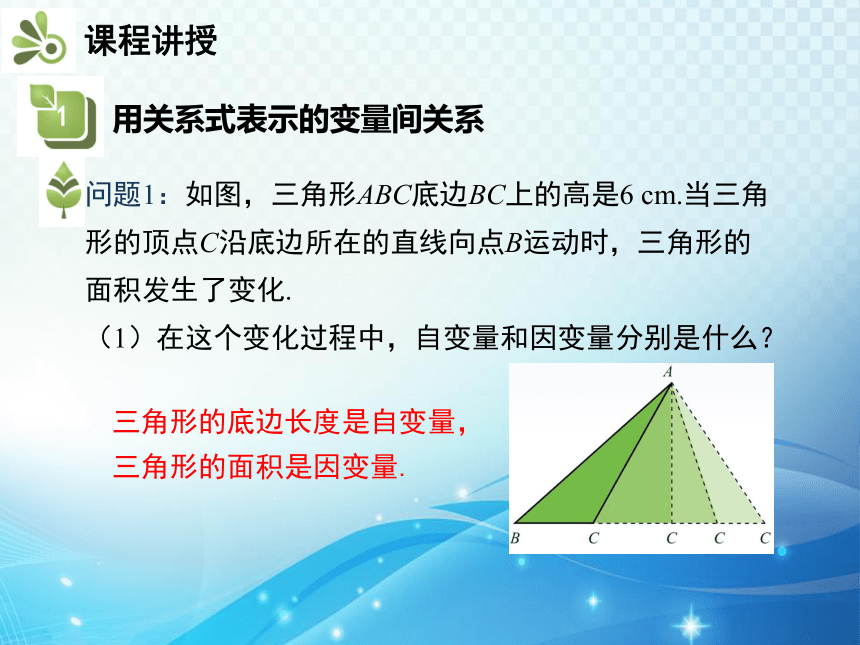
问题1:如图,三角形ABC底边BC上的高是6 cm.当三角形的顶点C沿底边所在的直线向点B运动时,三角形的面积发生了变化.
(1)在这个变化过程中,自变量和因变量分别是什么?
三角形的底边长度是自变量,
三角形的面积是因变量.
课程讲授
1
用关系式表示的变量间关系
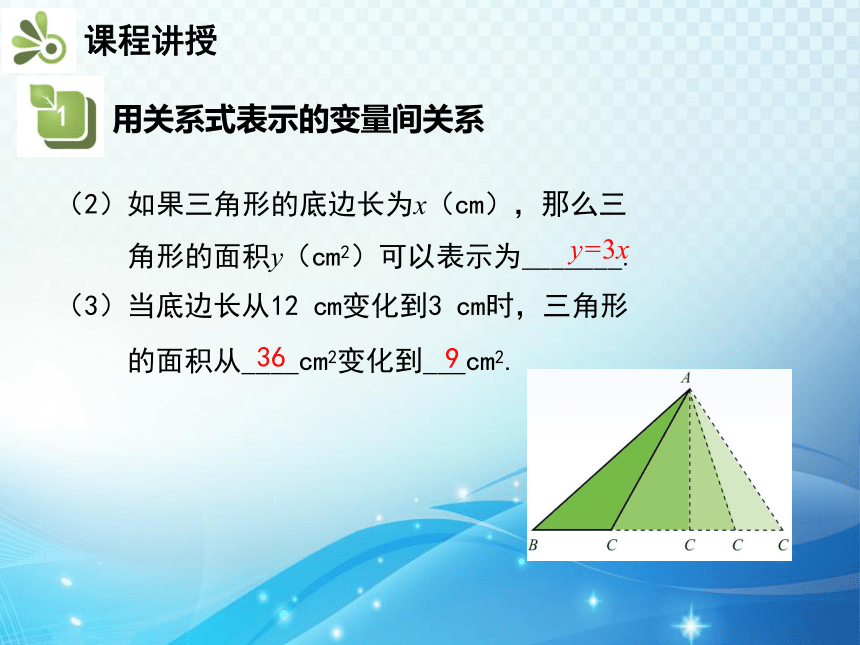
(2)如果三角形的底边长为x(cm),那么三
角形的面积y(cm2)可以表示为_______.
y=3x
(3)当底边长从12 cm变化到3 cm时,三角形
的面积从____cm2变化到___cm2.
36
9
课程讲授
1
用关系式表示的变量间关系
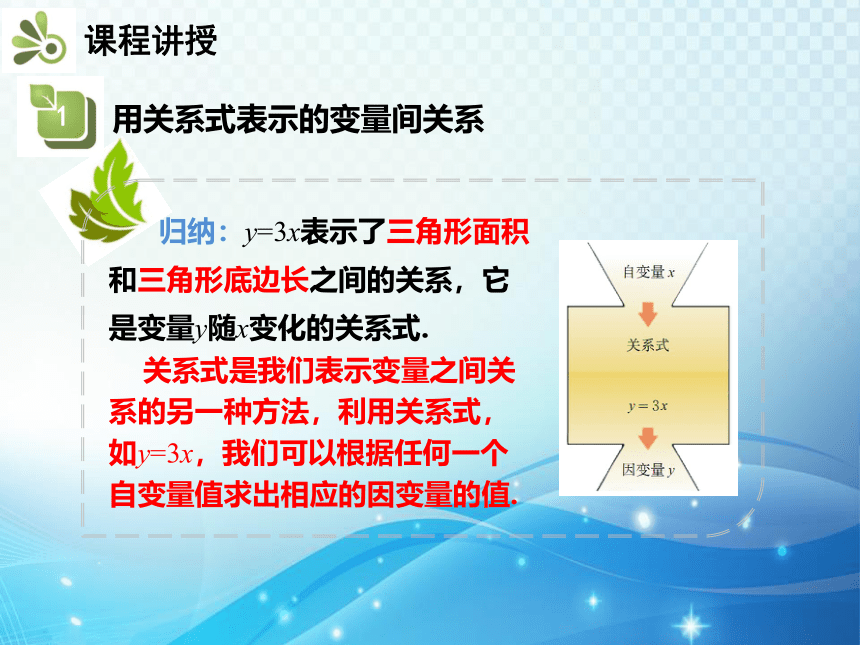
归纳:y=3x表示了三角形面积
和三角形底边长之间的关系,它
是变量y随x变化的关系式.
关系式是我们表示变量之间关
系的另一种方法,利用关系式,
如y=3x,我们可以根据任何一个
自变量值求出相应的因变量的值.
课程讲授
1
用关系式表示的变量间关系
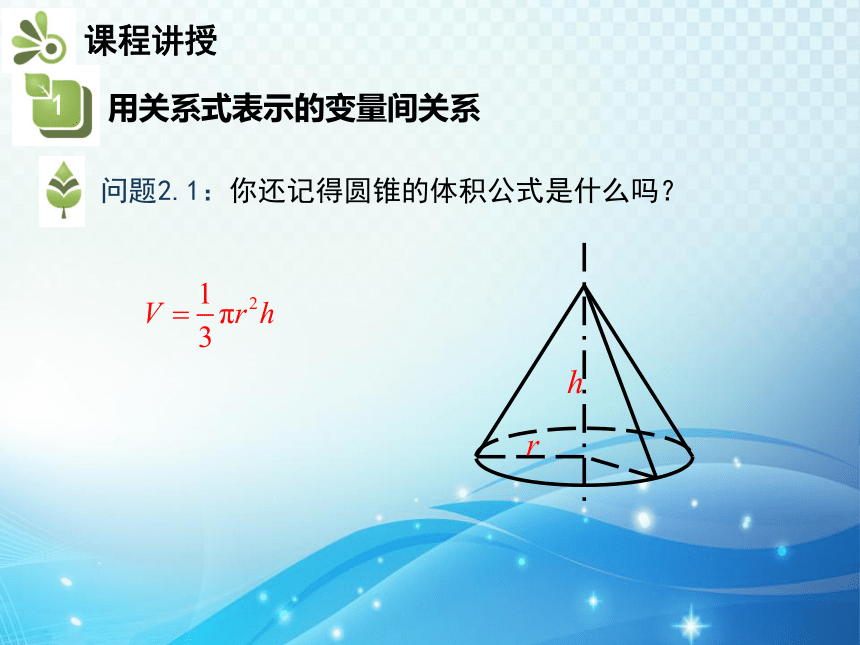
问题2.1:你还记得圆锥的体积公式是什么吗?
r
h
课程讲授
1
用关系式表示的变量间关系
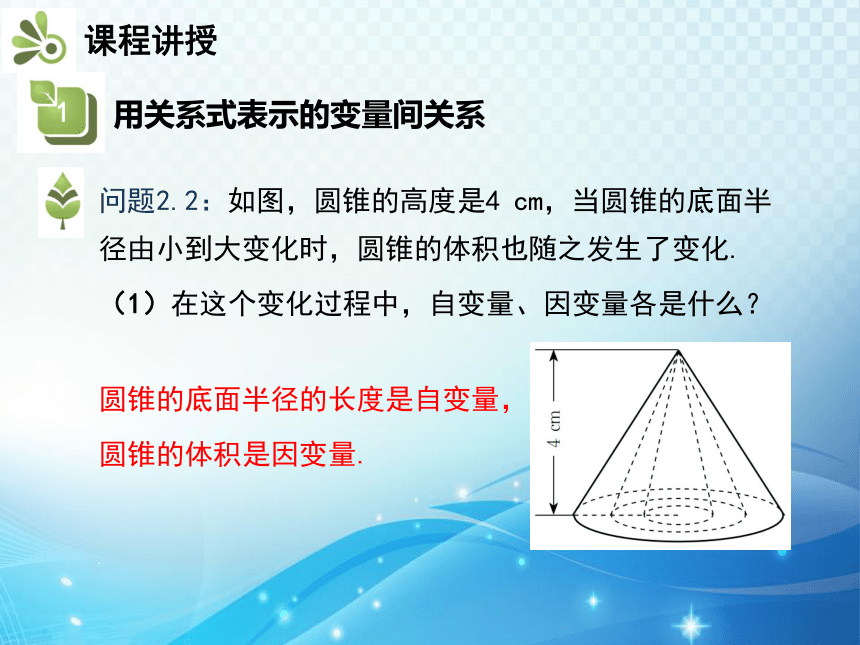
问题2.2:如图,圆锥的高度是4 cm,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化.
(1)在这个变化过程中,自变量、因变量各是什么?
圆锥的底面半径的长度是自变量,
圆锥的体积是因变量.
课程讲授
1
用关系式表示的变量间关系
(2)如果圆锥底面半径为 r(cm),那么圆锥的体
积V(cm3)与r的关系式为________.
(3)当底面半径由1 cm变化到10 cm时,圆锥的体
积由 cm3变化到 cm3 .
课程讲授
1
用关系式表示的变量间关系
练一练:据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05 ml.小康同学洗手后,没有把水龙头拧紧,水龙头以测试时的速度滴水,当小康离开x分钟后,水龙头滴出y ml的水,则y与x的关系式是( )
A. y=0.05x
B. y=5x
C. y=100x
D. y=0.05x+100
B
课程讲授
2
根据关系式求值
问题1:你知道什么是“低碳生活”吗?“低碳生活”
是指人们生活中尽量减少所耗能量,从而降低碳(特别是二氧化碳)的排放量的一种方式.
课程讲授
2
根据关系式求值
(1)家居用电的二氧化碳排放量可以用关系式
表示为_________,其中的字母分别表
示________________________.
y=0.785x
二氧化碳排放量、耗电量
课程讲授
2
根据关系式求值
(2)在上述关系式中,耗电量
每增加1 KW·h,二氧化
碳排放量增加_________.
当耗电量从1 KW·h增加到
100 KW·h时,二氧化碳排
放量从_________增加到
_________.
0.785 kg
78.5 kg
0.785 kg
课程讲授
2
根据关系式求值
(3)小明家本月用电大约110 kW·h、天然气20 m3、自来水5 t、油耗75 L,请你计算一下小明家这几项的二氧化碳排放量.
家居用电的二氧化碳:
110×0.785=86.35(kg)
开私家车的二氧化碳:
75×2.7=202.5(kg)
家用天然气的二氧化碳:
20×0.19=3.8(kg)
家用自来水的二氧化碳:
5×0.91=4.55(kg)
随堂练习
1.某同学带100元钱去买书,已知每册定价8.2元,买书
后剩余的钱y(元)和买的册数x的关系式是( )
A. y=8.2x
B. y=100-8.2x
C. y=8.2x-100
D. y=100+8.2x
B
随堂练习
2.一个长方形的周长为60 cm,其中一条边为x cm
(其中x>0),面积为y cm2 ,则y与x的关系式为
( )
A. y=60x-2x2
B. y=30x-x2
C. y=x2-60
D. y=x2-30
B
随堂练习
3.如果用c表示摄氏温度,f表示华氏温度,则c与f 之
间的关系为c= (f-32).
(1)当f=68时,c的值为 ,当f=-4时,c的值
为 ;
(2)当c=10时,f的值为 .
20
-20
50
随堂练习
4.商店出售一种瓜子,质量x(g)与售价c(元)之间
的关系如下表:
上表中售价栏中的0.1是塑料袋的价钱.
(1)写出售价c(元)与质量x(g)之间的关系式;
解:(1)c=0.009x+0.1.
随堂练习
(2)当质量在1 kg到3 kg之间变化时,售价的 变化
范围是多少元
解:(2)当x=1 kg时,c=9.1元,当x=3 kg时,c= 27.1元,所以售价的变化范围为9.1元至27.1元.
课堂小结
用关系式表示的变量间关系
根据表格中所列的数据,归纳总结两个变量的关
系式.
利用公式写出两个变量之间的关系式,比如各类
几何图形的周长、面积、体积公式等.
结合实际问题写出两个变量之间的关系式,比如
销量×(售价-进价)=利润等.
3.2 用关系式表示的变量
间关系
第三章 变量之间的关系
课程讲授
新知导入
随堂练习
课堂小结
知识要点
1.用关系式表示的变量间关系
2.根据关系式求值
新知导入
想一想:
在“小车下滑的时间”中,
1.支撑物的高度h和小车下滑的时间t都在变化,
它们都是变量.其中小车下滑的时间t随支撑物
的高度h的变化而变化;
2.支撑物的高度h是自变量;
3.小车下滑的时间t是因变量.
课程讲授
1
用关系式表示的变量间关系
问题1:如图,三角形ABC底边BC上的高是6 cm.当三角形的顶点C沿底边所在的直线向点B运动时,三角形的面积发生了变化.
(1)在这个变化过程中,自变量和因变量分别是什么?
三角形的底边长度是自变量,
三角形的面积是因变量.
课程讲授
1
用关系式表示的变量间关系
(2)如果三角形的底边长为x(cm),那么三
角形的面积y(cm2)可以表示为_______.
y=3x
(3)当底边长从12 cm变化到3 cm时,三角形
的面积从____cm2变化到___cm2.
36
9
课程讲授
1
用关系式表示的变量间关系
归纳:y=3x表示了三角形面积
和三角形底边长之间的关系,它
是变量y随x变化的关系式.
关系式是我们表示变量之间关
系的另一种方法,利用关系式,
如y=3x,我们可以根据任何一个
自变量值求出相应的因变量的值.
课程讲授
1
用关系式表示的变量间关系
问题2.1:你还记得圆锥的体积公式是什么吗?
r
h
课程讲授
1
用关系式表示的变量间关系
问题2.2:如图,圆锥的高度是4 cm,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化.
(1)在这个变化过程中,自变量、因变量各是什么?
圆锥的底面半径的长度是自变量,
圆锥的体积是因变量.
课程讲授
1
用关系式表示的变量间关系
(2)如果圆锥底面半径为 r(cm),那么圆锥的体
积V(cm3)与r的关系式为________.
(3)当底面半径由1 cm变化到10 cm时,圆锥的体
积由 cm3变化到 cm3 .
课程讲授
1
用关系式表示的变量间关系
练一练:据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05 ml.小康同学洗手后,没有把水龙头拧紧,水龙头以测试时的速度滴水,当小康离开x分钟后,水龙头滴出y ml的水,则y与x的关系式是( )
A. y=0.05x
B. y=5x
C. y=100x
D. y=0.05x+100
B
课程讲授
2
根据关系式求值
问题1:你知道什么是“低碳生活”吗?“低碳生活”
是指人们生活中尽量减少所耗能量,从而降低碳(特别是二氧化碳)的排放量的一种方式.
课程讲授
2
根据关系式求值
(1)家居用电的二氧化碳排放量可以用关系式
表示为_________,其中的字母分别表
示________________________.
y=0.785x
二氧化碳排放量、耗电量
课程讲授
2
根据关系式求值
(2)在上述关系式中,耗电量
每增加1 KW·h,二氧化
碳排放量增加_________.
当耗电量从1 KW·h增加到
100 KW·h时,二氧化碳排
放量从_________增加到
_________.
0.785 kg
78.5 kg
0.785 kg
课程讲授
2
根据关系式求值
(3)小明家本月用电大约110 kW·h、天然气20 m3、自来水5 t、油耗75 L,请你计算一下小明家这几项的二氧化碳排放量.
家居用电的二氧化碳:
110×0.785=86.35(kg)
开私家车的二氧化碳:
75×2.7=202.5(kg)
家用天然气的二氧化碳:
20×0.19=3.8(kg)
家用自来水的二氧化碳:
5×0.91=4.55(kg)
随堂练习
1.某同学带100元钱去买书,已知每册定价8.2元,买书
后剩余的钱y(元)和买的册数x的关系式是( )
A. y=8.2x
B. y=100-8.2x
C. y=8.2x-100
D. y=100+8.2x
B
随堂练习
2.一个长方形的周长为60 cm,其中一条边为x cm
(其中x>0),面积为y cm2 ,则y与x的关系式为
( )
A. y=60x-2x2
B. y=30x-x2
C. y=x2-60
D. y=x2-30
B
随堂练习
3.如果用c表示摄氏温度,f表示华氏温度,则c与f 之
间的关系为c= (f-32).
(1)当f=68时,c的值为 ,当f=-4时,c的值
为 ;
(2)当c=10时,f的值为 .
20
-20
50
随堂练习
4.商店出售一种瓜子,质量x(g)与售价c(元)之间
的关系如下表:
上表中售价栏中的0.1是塑料袋的价钱.
(1)写出售价c(元)与质量x(g)之间的关系式;
解:(1)c=0.009x+0.1.
随堂练习
(2)当质量在1 kg到3 kg之间变化时,售价的 变化
范围是多少元
解:(2)当x=1 kg时,c=9.1元,当x=3 kg时,c= 27.1元,所以售价的变化范围为9.1元至27.1元.
课堂小结
用关系式表示的变量间关系
根据表格中所列的数据,归纳总结两个变量的关
系式.
利用公式写出两个变量之间的关系式,比如各类
几何图形的周长、面积、体积公式等.
结合实际问题写出两个变量之间的关系式,比如
销量×(售价-进价)=利润等.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
