中考总复习-因式分解[下学期]

课件22张PPT。中考数学总复习
数 与 式第一章第四课时：
因式分解 要点、考点聚焦
课前热身
典型例题解析
课时训练因
式
分
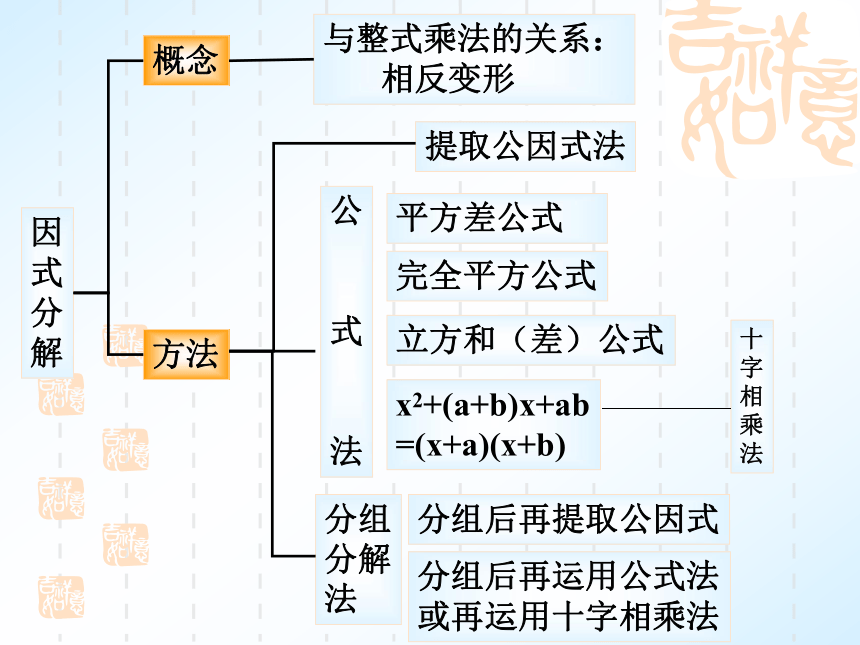
解概念方法与整式乘法的关系：
相反变形提取公因式法公
式
法平方差公式 完全平方公式立方和（差）公式x2+(a+b)x+ab
=(x+a)(x+b)十
字
相
乘
法分组
分解
法分组后再提取公因式分组后再运用公式法
或再运用十字相乘法要点、考点聚焦2.因式分解的几种常用方法
(1)提公因式法
(2)运用公式法：
①平方差公式：a2-b2=(a+b)(a-b)
②完全平方公式：a2±2ab+b2=(a±b)2
③立方和与立方差公式:
(ａ＋ｂ)(ａ2－ａｂ＋ｂ2)＝ａ3＋ｂ3，
(ａ－ｂ)(ａ2＋ａｂ＋ｂ2)＝ａ3－ｂ3.
(3)二次三项式型：x2+(a+b)x+ab=(x+a)(x+b)
(4)分组分解法：
①分组后能提公因式；②分组后能运用公式.1.因式分解的定义
把一个多项式化为n个整式的积的形式，叫做把这个
多项式因式分解或分解因式.因式分解须进行到每个因式不能再继续分解为止。分解因式与整式乘法是互逆过程.
分解因式要注意以下几点:
1.分解的对象必须是多项式.
2.分接的结果一定是几个整式
的乘积的形式.
3.有公因式的必须先提公因式。
4.要分解到不能分解为止.几点注意：
（1）、在多项式中找公因式应对系数和字母分别考虑，公因式的系数是各项系数 的最大公约数，字母是各项相同的字母 ，字母的指数取最低的。
（2）、提取公因式的依据是乘法分配律的逆用。
（3）、提取公因式要一次提尽。3.因式分解的一般步骤
可归纳为一“提”、二“运”、三“分”、四“十字”：
(1)一“提”：先看多项式的各项是否有公因式，若有
必须先提出来.
(2)二“运”：若多项式的各项无公因式(或已提出公
因式)，第二步则看能不能用公式法分解.
(3)“三分”：若以上两步都不行，则应考虑分组分解法，将能用上述方法进行分解的项分成一组，使之分组后能“提”或能“运”，当然要注意其要分解到底才能结束.
(4)四“十字”：若以上三步都不行，则应考虑用x2+(p+q)x+pq型分解.要点、考点聚焦分解因式必须严格按照上述步骤进行，且必须分解彻底！关于分解因式的方法把一个多项式分解因式，首先观察这个多项式的特点，选用适当的方法分解因式.
1、当所给的多项式的各项有公因式时，应先提公因式；
2、当一个多项式是两项（或可以化成两项）的平方差形式时，就选用平方差公式；
3、当一个多项式是完全平方式（或可以转化为完全平方式）时，就选用完全平方公式；
4、当一个多项式两个平方项都含有负号时，先提出负号，使括号内的多项式的平方项变为正号；
4、当多项式是二次三项式（或可以看作是二次三项式）时，通过变换，把这个多项式转化为完全平方式，再进行分解因式.3.下列多项式中，能用提公因式法分解因式的是( )
A.x2-y B.x2+2x
C.x2+y2 D.x2-xy+y2 课前热身1.(2004年·南京)分解因式：3x2-3= . 2.(2004·河北)分解因式：
X2+2xy+y2-4= . 3(x+1)(x-1)(x+y+2)(x+y-2)B4.(2004年·济南)分解因式：a2-4a+4= . (a-2)25.(2004年·桂林)分解因式：a3+2a2+a= .6.(2004年·呼和浩特)将下列式子因式分解
x-x2-y+y2= .a(a+1)2(x-y)(1-x-y)课前热身7.(2004年·大连试验区)关于x的一元二次方程x2+bx+c=0
的两根为x1＝1，x2＝2，则x2+bx+c分解因式的结果为：
. 8.(2004年·北京市)分解因式：
x2-4y2+x-2y= . (x-2y)(1+x+2y)课前热身（x-1）(x-2)典型例题解析【例1】 因式分解：
(1)-4x2y+2xy2-12xy；
(2)3x2(a-b)-x(b-a)；
(3)9(x+y)2-4(x-y)2；解：
(1)原式=-2xy(2x-y+6)(2)原式=3x2(a-b)+x(a-b)
=x(a-b)(3x+1)(3)原式=［3(x+y)+2(x-y)］［3(x+y)-2(x-y)］
=(5x+y)(x+5y)解：(4)原式=(9a2)2-1２
=(9a2+1)(9a2-1)
=(3a+1)(3a-1)(9a2+1)典型例题解析【例1】 因式分解：
(4)81a4-1；
(5)(x2+2x)2+2(x2+2x)+1；
(6)(a2+b2)2-4a2b2.(5)原式=(x2+2x+1)2=(x+1)4(6)原式=(a２+b2+2ab)(a2+b2-2ab)
=(a+b)2(a-b)2【例2】 因式分解：-3an-1+12an-12an+1
(n＞1的正整数). ?解：原式=-3an-1［1-4an-(n-1)+4a(n+1)-(n-1)］
=-3an-1(1-4a+4a2)
=-3an-1(2a-1)2【例3】 因式分解：
(1)m3+2m2-9m-18；典型例题解析解：(1)
原式=(m3+2m2)-(9m+18)
=m2(m+2)-9(m+2)
=(m+2)(m2-9)
=(m+2)(m-3)(m+3)或者：
原式=(m3-9m)+(2m2-18)
=m(m2-9)+2(m2-9)
=(m2-9)(m+2)
=(m-3)(m+3)(m+2)解：
(2)原式=a2-(b2+2bc+c2)
=a2-(b+c)2
=(a+b+c)(a-b-c)(3)原式=(x2)2-5(x2)+4
=(x2-4)(x2-1)
=(x-2)(x+2)(x-1)(x+1)
(4)原式=x3-x2-x2-5x+6
=x2(x-1)-(x2+5x-6)
=x2(x-1)-(x+6)(x-1)
=(x-1)(x2-x-6)
=(x-1)(x-3)(x+2)典型例题解析【例3】 因式分解：
(2)a2-b2-c2-2bc；
(3)x4-5x2+4；
(4)x3-2x2-5x+6.【例4】 求证：对于正整数n，2n+4-2n能被30整除. 解：2n+4-2n=2n(2４-1)=2n(16-1)=15×2n
=15×2×2n-1=30×2n-1.
∵n为正整数时，2n-1为整数，
∴2n+4-2n能被30整除.
【例5】 分解因式：x3+6x2+11x+6. 解：方法一：原式=x3+3x2+3x2+9x+2x+6
=x2(x+3)+3x(x+3)+2(x+3)
=(x+3)(x2+3x+2)
=(x+3)(x+1)(x+2)典型例题解析方法二：原式=x3+2x2+4x2+8x+3x+6
=x2(x+2)+4x(x+2)+3(x+2)
=(x+2)(x2+4x+3)
=(x+2)(x+1)(x+3)
方法三：原式=x3+x2+5x2+5x+6x+6
=x2(x+1)+5x(x+1)+6(x+1)
=(x+1)(x2+5x+6)
=(x+1)(x+2)(x+3)方法四：原式=(x3+5x2+6x)+(x2+5x+6)
=x(x2+5x+6)+(x2+5x+6)
=(x2+5x+6)(x+1)
=(x+2)(x+3)(x+1) 典型例题解析1.因式分解应进行到底.
如：在实数范围内分解因式：
x4-4=(x2+2)(x2-2)
=(x2+2)(x+ )(x- ).
应在实数范围内将它分解到底.方法小结：2.不要将因式分解的结果又用整式的乘法展开而还原.
如:(a2+b2)２-4a2b2
=(a2+b2+2ab)(a2+b2-2ab)
=(a+b)2(a-b)2
=［(a+b)(a-b)］2
=(a2-b2)2
=a4-2a2b2+b4
实际该题到第2个等于号就分解到底了，不能再向下
计算了!
方法小结：3.注意解题的技巧的应用，不能死算.
如：分解因式(x+1)(x+3)(x+5)(x+7)-9
=［(x+1)(x+7)］［(x+3)(x+5)］-9
=(x2+8x+7)(x2+8x+15)-9
=［(x2+8x)+7］［(x2+8x)+15］-9
=(x2+8x)2+22(x2+8x)+105-9
=(x2+8x)2+22(x2+8x)+96
=(x2+8x +6)(x2+8x +16)
=(x2+8x+6)(x+4)2
方法小结：课时训练1.(2004年·福州市)分解因式：a2-25= .2. (2004年·陕西)分解因式：x3y2-4x= .3. (2004年·长沙)分解因式：xy2-x2y= . x(xy+2)(xy-2)(a+5)(a-5)xy(y-x) y(x-2)24. (2004年·青海)分解因式：x2y-4xy+4y= . 5. (2004年·哈尔滨)分解因式：
a2-2ab+b2-c2= . (a-b+c)(a-b-c)7. (2004年·北京)多项式ac-bc+a2-b2分解因式的结果为
( )
A. (a-b)(a+b+c) B. (a-b)(a+b-c)
C. (a+b)(a+b-c) D. (a+b)(a-b+c)8. (2004年·宁夏)把多项式1-x2+2xy-y2分解因式的结
果为 ( )
A.(1-x-y)(1+x-y) B.(1+x-y)(1-x+y)
C.(1-x-y)(1-x+y) D.(1+x-y)(1+x+y)
?AB课时训练6. (2004年·甘肃)为使x2-7x+b在整数范围内可以分解
因式，则b可能取的值为 . （任写一个）