因式分解[下学期]

北师大版八年级下册课堂同步练习 第二章 分解因式
第二章分解因式
1分解因式
一、预习检测
1、把一个 化成几个 的形式，这种变形叫做把这个多项式分解因式。
2、在下列运算中，从左到右的变形是乘法运算的是（ ）
A、 B、
C、 D、
3、下列等式中，从左到右的变形属于分解因式的是（ ）
A、 B、
C、 D、
4、连一连：
5、能被120整除吗？说明你的理由。
二、课堂检测
1、下列各式从左到右的变形中，哪些是分解因式？
① ②
③ ④
⑤ ⑥
2、计算：
3、连一连：
4、（1）能被2006整除吗？能被2007整除吗？2）能被4整除吗？
5、某环保局为改变绿化环境，计划拨款给东区ma万元，给中区mb万元，给西区mc万元，当m=5.7，a=2.1，b=3.5，c=4.4时，问环保局一共拨款多少万元？
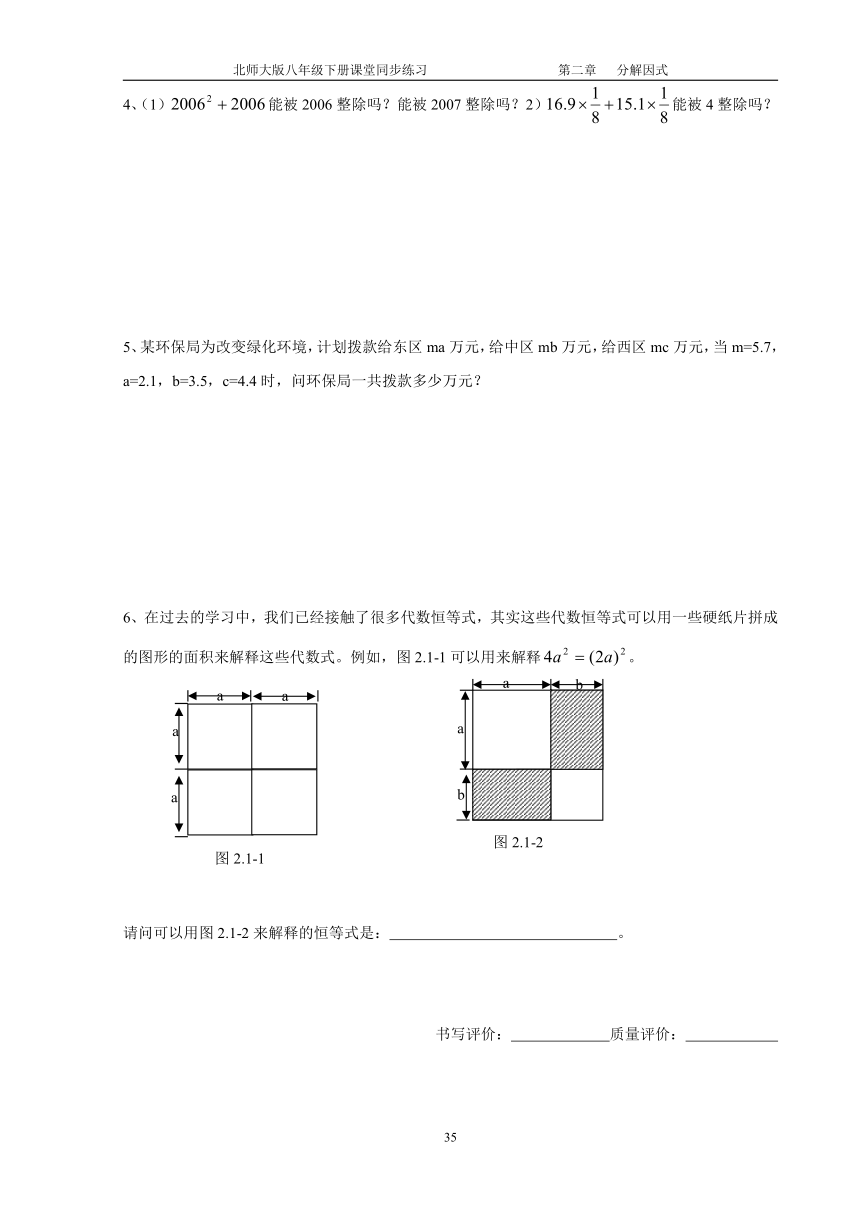
6、在过去的学习中，我们已经接触了很多代数恒等式，其实这些代数恒等式可以用一些硬纸片拼成的图形的面积来解释这些代数式。例如，图2.1-1可以用来解释。
请问可以用图2.1-2来解释的恒等式是： 。
书写评价： 质量评价：
2提公因式（1）
一、预习检测
1、如果一个多项式的各项含有公因式，那么就可以把这个 提出来，从而将多项式化成两个因式的 的形式，这种因式分解的方法叫做提公因式法。
2、请写出下列多项式的公因式：
① ②
③ ④
⑤ ⑥
3、把分解因式时，正确结果是（ ）
A、 B、
C、 D、
4、把下列各式分解因式：
① ②
③ ④
⑤ ⑥
二、课堂检测
1、把下列各式分解因式：
① ②
③ ④
⑤ ⑥
2、单项式与的公因式是： 。
3、多项式的公因式是 ，提公因式后，另一个因式是 。
4、若分解因式，则的值为（ ）
A、-5 B、5 C、-2 D、2
5、利用分解因式进行计算：
（1）
（2）
（3），其中=20，=16，=12，。
（4），其中，
6、若两个孩子的年龄分别是、，已知=99，试求这两个孩子的年龄。
书写评价： 质量评价：
3提公因式（2）
一、预习检测
1、在下列各式等号右边的括号前填入“+”或“-”号，使等式成立：
① ②
③ ④
⑤ ⑥
2、多项式的公因式是
3、填空
（1）（ ）
（2）（ ）
4、把下列各式分解因式：
① ②
③ ④
⑤ ⑥
二、课堂检测
1、多项式分解因式正确的是（ ）
A、 B、
C、 D、
2、把下列各式分解因式：
① ②
③ ④
⑤ ⑥
⑦ ⑧
3、先分解因式，再计算求值：
（1），其中，
（2），其中
4、计算下列各题：
（1） （2）
5、已知，，求的值。
6、先阅读下面例子，再解答问题
求满足的值。
解：原方程可变形为，
或，所以，
请仿照上面例子，求满足的值。
书写评价： 质量评价：
4运用公式法（1）
一、预习检测
1、填空（把下列各式写成完全平方的形式）
①= ②=
③= ④=
⑤= ⑥=
2、某多项式分解因式结果为，那么这个多项式是（ ）
A、 B、 C、 D、
3、下列各式中，能运用平方差公式分解因式的是（ ）
A、 B、 C、 D、
4、判断下面从左到右的变形是否正确
① ②
③ ④
5、把下列各式分解因式
① ②
③ ④
二、课堂检测
1、下列各式中含有因式的是（ ）
A、 B、 C、 D、
2、分解因式结果是（ ）
A、0 B、 C、 D、
3、把下列各式分解因式
① ②
③ ④
⑤ ⑥
⑦ ⑧
4、利用平方差公式计算下列各题
（1） （2）
5、如图，大小两圆的圆心相同，已知它们的半径分别是
和，求它们所围成的环形的面积。如果，
呢？（）
6、观察下列各式：
……
（1）根据前面的规律可得
（2）请按以上规律分解因式：
书写评价： 质量评价：
5运用公式法（2）
1、 预习检测
1、判断下列多项式是不是完全平方式
① （ ） ② （ ）
③ （ ） ④ （ ）
⑤ （ ） ⑥ （ ）
2、若是完全平方式，则的值为（ ）
A、4 B、8 C、16 D、32
3、下列多项式中，能用公式法进行因式分解的是（ ）
A、 B、 C、 D、
4、把下列各式分解因式：
① ②
③ ④
二、课堂检测
1、对分解因式，结果正确的是（ ）
A、 B、 C、 D、
2、若多项式是完全平方式，则的值是（ ）
A、3 B、5 C、-3或5 D、3或-5
3、把下列各式分解因式：
① ②
③ ④
⑤ ⑥
⑦ ⑧
4、已知，，求代数式的值。
5、利用完全平方公式计算下列各题
（1） （2）
6、两个连续奇数的平方差能被8整除吗？为什么？
7、已知、、为△ABC的三边的长，请判断多项式与0的大小关系。
书写评价： 质量评价：
第二章《回顾与复习》一
1、 知识结构：
1、把一个 化成 的形式叫因式分解。
2、下列由左到右的变形，是因式分解的为（ ）
A、 B、
C、 D、
3、多项式含有的 叫做这个多项式的公因式。
4、多项式的公因式是 。
5、分解因式为( )
(A) (B)
(C) (D)
6、分解因式的结果是( )
(A) (B)
(C) (D)
7、分解因式的结果是( )
(A) (B)
(C) (D)
8、分解因式的方法有 、 ；其中
包括有 、 。
9、下列各式中，能用平方差分解因式的是（ ）
A、 B、 C、 D、
10、下列各式中是完全平方式的是（ ）
A、 B、
C、 D、
11、多项式分解因式后其中的一个因式是（ ）
A、 B、 C、 D、
12、多项式 分解因式的结果是 。
13、（ ）（ ）
14、若是完全平方式；则t＝__________．
15、多项式有（ ）个因式
A .2 B. 3 C.4 D.5
16、若则（　　　）
A.a=1,b=3 B.a=1,b=-3 C.a=-1,b=3 D.a=-1,b=-3
17、把多项式分解因式，结果正确的是 ( )
A． B．
C． D．
2、 解答题：
18） 19）
20） 21）
22） 23）
24）已知，，求的值
书写评价： 质量评价：
第二章《回顾与复习》二
1、 选择题：（3分/题共15分）
1、下列各式从左到右的变形错误的是( )
(A) (B)
(C) (D)
2、把多项式分解因式时，应提取的公因式为（ ）
A、 B、 C、 D、
3、下列各式从左到右是分解因式的是（ ）
A． B.
C . D .
4、已知多项式＝（x-1）2 ，则k值为( )
(A)-3 (B)1 (C)-1 (D) 不能确定
5、下列各式是完全平方式的是( )
(A) (B)
(C) (D)
2、 填空题：（3分/题共15分）
6、=____)_____)
7、 ______=)(
8、________=
9、若为一完全平方式，则m=________。
10、若，则。
3、 解答题：（6分/题共36分）
11、 12、
13、 14、
15、 16、1003×997
17、已知，求的值（10分）
18、若矩形的面积是其中一条边长为，求矩形的另一条边长的代数式。（12分）
19、已知724－1可被40至50之间的两个整数整除，请求出这两个整数。（12分）
书写评价： 质量评价：
第二章《回顾与复习》三
一、选择题：（3分/题共15分）
1、分解因式的结果是( )
(A) (B)
(C) (D)
2、下列变形正确的有（ ）
①②③
④⑤
⑥
A、2个 B、3个 C、4个 D、5个
3、下列多项式中不含有因式(x－1)的是 ()
A． B．
C． D．
4、两个连续奇数的平方差是（ ）
16的倍数 B、12的倍数 C、8的倍数 D、4的倍数
5、不论a,b为任何实数的值总是（ ）
A. 负数 B .0 C.正数　　　　　　 D.非负数
3、 空题：（3分/题共15分）
6、_____+9=（+_______
7、的值是 。
8、若多项式 因式分解为(x+1)(x-2)，则a= ,b= 。
9、分解因式________.
10、已知是完全平方式，则k=________.
解答题：（6分/题共36分）
11、 12、；
13、 14、
15、 16、
17、已知的值为0，求的值。（10分）
18、求证：无论a,b为何值时，代数式的值均为正值。（12分）
19、如图，在一块边长为a厘米的正方形纸板四角，各剪去一个边长为 b(b<)厘米的正方形，利用因式分解计算当a=13.2，b=3.4时，剩余部分的面积。（12分）
书写评价： 质量评价：
x2-y2
9-25x2
x2+2x+1
xy-y2
(x+y)(x-y)
(3-5y)(3+5y)
y(x-y)
(x+1)2
(2a-1)(2a+1)
(x-1)2
(x+2)2
(x-1)(x+1)
x2+4x+4
x2-2x+1
4a2-1
x2-1
a
a
a
a
图2.1-1
a
a
b
b
图2.1-2
R
r
35