因式分解的复习[下学期]
图片预览



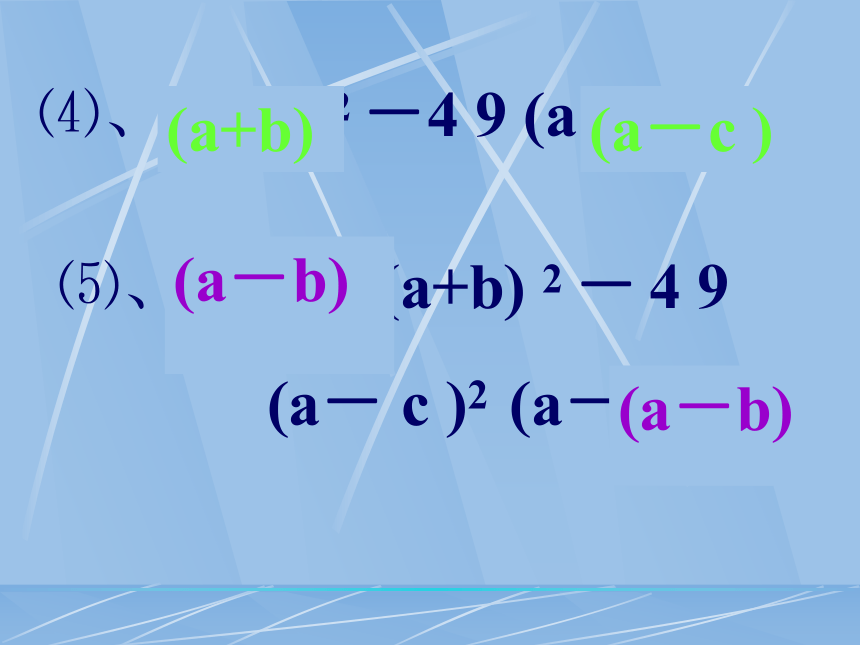





文档简介
课件25张PPT。欢迎光临 多谢指导 因式分解复习执教者:端木敏捷例1、 分解因式:
⑴、 x2 -49y2
⑵、 x 3 - 49 x y23x ⑶、x2 (a-b) +49y2 (b-a)
(a-b) (b-a)
⑷、(a+b) 2 -4 9 (a-c ) 2
(a+b)(a-c ) ⑸、(a-b) (a+b) 2 - 4 9
(a- c )2 (a-b)
(a-b)
(a-b)
例2、 分解因式:
⑴、2x2 + x - 3;
⑵、2x2 y2 + xy - 3;
⑶、2x2 + xy - 3y2 ;
⑷、2x4+ x2 - 3;
⑸、2(a - b)2 + a - b- 3.
例3、 分解因式:
⑴、x3 - x2 - x+1;
⑵、 x 4 - x3 - x2 + x;
⑶、 p x2 - p3 -px -p 2.例4、 分解因式:
⑴、x2+3x +2+mx+2m;⑵、2x2+3x +mx+2m - 2;
例5、 分解因式:
⑴、a2 -2ab+b2 - 36;⑵ 、a2 - b2 - 12b- 36; ⑶、 a2 - b2 + 12b- 36; ⑷、1 - a2 - b2 + 2ab.例6、 分解因式:
⑴、 2(a - b)2 + a - b- 3;
=[(a-b)-1][2(a-b)+3]
=(a-b-1) (2a-2b+3)
⑵、 2(a - b)2 + b - a - 3;⑶、2a 2+4ab+ 2b 2 + a+b-3;
⑷、a2+2ab+b2+5a+5b- 36;
⑸、2a2+4ab+2b2+5a+5b-3.
例7、为使多项式x2+ax-12能因式分解,a分别可以取哪些整数?且把a取不同值时所对应的多项式分解因式的结果写出来.
答: a 可以取±11,±4,±1
例7、为使多项式x2+ax-12能因式分 解,a分别可以取哪些整数?且把a取不同值时所对应的多项式分解因式的结果写出来.
答: a 可以取±11,±4,±1
练习:为使多项式x2+4x+a能因式分解,a分别可以取哪些整数?且把a取不同值时所对应的多项式分解因式的结果写出来.(至少写出六条)
例8、分解因式:
⑴ 、 x2 +x-12 计 算: ( )÷
( x- 3) ⑶、( x3 +x 2 -12x)÷
(x- 3)
⑵、( x3 +x 2 -12x)÷
(x2- 3x)
例9、解方程:x2+x-12=0.
变式⑴、:x2+x=12;
变式⑵、:x(x+1)-12=0;
变式⑶、:x(x+1)=12; 变式⑷、:(x+2)(x - 1)=10.
当 a =11 时:
x2+ax-12
= x2+11x-12= (x-1)
(x+12)
当 a = - 11 时:
x2+ax-12
= x2-11x-12
=(x+1)(x-12)
当 a =4 时:
x2+ax-12
= x2+4x-12
=(x+6)(x-2)
当 a = - 4 时:
x2+ax-12
= x2- 4x-12
=(x- 6)(x+2)
当 a = 1 时:
x2+ax-12
= x2+x-12
=(x+4)(x-3)
当 a = - 1 时:
x2+ax-12
= x2- x-12
=(x-4)(x+3)
因式分解的思路:要想分解多项式,先看有无公因式;其次查对各公式; 遇到二次三项式,十字相乘试一试;四项以上多项式,
分组分解试一试;因式分解到最后, 结果应是最简式。例10、两个长方形的长和宽
分别都是1.7cm和1.3cm,且两个
正方形的边长分别为1.7cm和1.3
cm. 求这四个图形的面积之和.再见2000年5月
⑴、 x2 -49y2
⑵、 x 3 - 49 x y23x ⑶、x2 (a-b) +49y2 (b-a)
(a-b) (b-a)
⑷、(a+b) 2 -4 9 (a-c ) 2
(a+b)(a-c ) ⑸、(a-b) (a+b) 2 - 4 9
(a- c )2 (a-b)
(a-b)
(a-b)
例2、 分解因式:
⑴、2x2 + x - 3;
⑵、2x2 y2 + xy - 3;
⑶、2x2 + xy - 3y2 ;
⑷、2x4+ x2 - 3;
⑸、2(a - b)2 + a - b- 3.
例3、 分解因式:
⑴、x3 - x2 - x+1;
⑵、 x 4 - x3 - x2 + x;
⑶、 p x2 - p3 -px -p 2.例4、 分解因式:
⑴、x2+3x +2+mx+2m;⑵、2x2+3x +mx+2m - 2;
例5、 分解因式:
⑴、a2 -2ab+b2 - 36;⑵ 、a2 - b2 - 12b- 36; ⑶、 a2 - b2 + 12b- 36; ⑷、1 - a2 - b2 + 2ab.例6、 分解因式:
⑴、 2(a - b)2 + a - b- 3;
=[(a-b)-1][2(a-b)+3]
=(a-b-1) (2a-2b+3)
⑵、 2(a - b)2 + b - a - 3;⑶、2a 2+4ab+ 2b 2 + a+b-3;
⑷、a2+2ab+b2+5a+5b- 36;
⑸、2a2+4ab+2b2+5a+5b-3.
例7、为使多项式x2+ax-12能因式分解,a分别可以取哪些整数?且把a取不同值时所对应的多项式分解因式的结果写出来.
答: a 可以取±11,±4,±1
例7、为使多项式x2+ax-12能因式分 解,a分别可以取哪些整数?且把a取不同值时所对应的多项式分解因式的结果写出来.
答: a 可以取±11,±4,±1
练习:为使多项式x2+4x+a能因式分解,a分别可以取哪些整数?且把a取不同值时所对应的多项式分解因式的结果写出来.(至少写出六条)
例8、分解因式:
⑴ 、 x2 +x-12 计 算: ( )÷
( x- 3) ⑶、( x3 +x 2 -12x)÷
(x- 3)
⑵、( x3 +x 2 -12x)÷
(x2- 3x)
例9、解方程:x2+x-12=0.
变式⑴、:x2+x=12;
变式⑵、:x(x+1)-12=0;
变式⑶、:x(x+1)=12; 变式⑷、:(x+2)(x - 1)=10.
当 a =11 时:
x2+ax-12
= x2+11x-12= (x-1)
(x+12)
当 a = - 11 时:
x2+ax-12
= x2-11x-12
=(x+1)(x-12)
当 a =4 时:
x2+ax-12
= x2+4x-12
=(x+6)(x-2)
当 a = - 4 时:
x2+ax-12
= x2- 4x-12
=(x- 6)(x+2)
当 a = 1 时:
x2+ax-12
= x2+x-12
=(x+4)(x-3)
当 a = - 1 时:
x2+ax-12
= x2- x-12
=(x-4)(x+3)
因式分解的思路:要想分解多项式,先看有无公因式;其次查对各公式; 遇到二次三项式,十字相乘试一试;四项以上多项式,
分组分解试一试;因式分解到最后, 结果应是最简式。例10、两个长方形的长和宽
分别都是1.7cm和1.3cm,且两个
正方形的边长分别为1.7cm和1.3
cm. 求这四个图形的面积之和.再见2000年5月
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
