人教版数学八年级下册18.1.1 平行四边形的性质 同步练习(含解析)
文档属性
| 名称 | 人教版数学八年级下册18.1.1 平行四边形的性质 同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 434.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 16:10:52 | ||
图片预览


文档简介
18.1.1 平行四边形的性质 同步练习
一、单选题
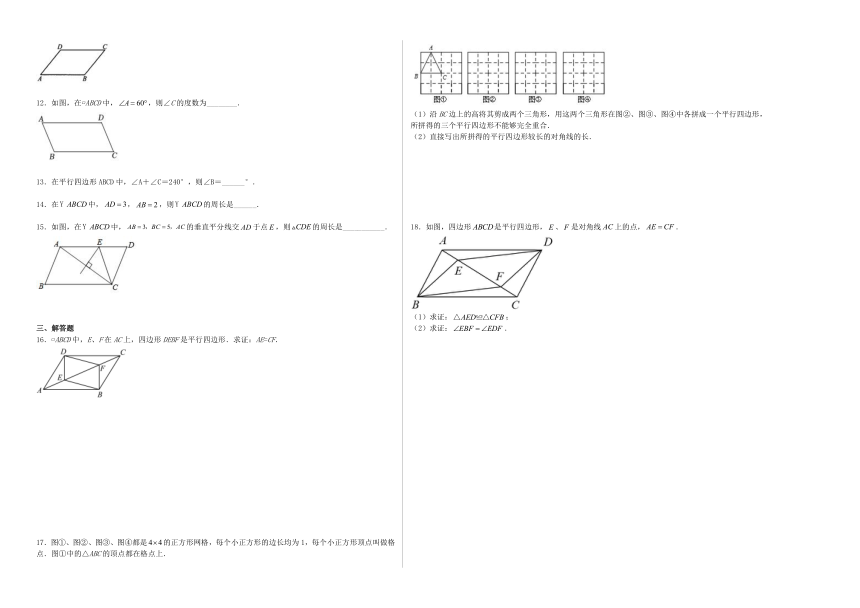
1.如图,已知在□ABCD中,∠A=154°,则∠B等于( )
A.154° B.46° C.36° D.26°
2.如图,□ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M,如果△CDM的周长是40cm,则平行四边形ABCD的周长是( )
A.40cm B.60cm C.70cm D.80cm
3.如图,O为坐标原点,△OAB是等腰直角三角形,∠OAB=90°,点B的坐标为(0,2),将该三角形沿x轴向右平移得到Rt△O′A′B′,此时点B′的坐标为(2,2),则线段OA在平移过程中扫过部分的图形面积为( )
A.2 B. C.4 D.
4.如图,在平行四边形ABCD中,∠B=70°,延长CD到点E,则∠1的度数为( )
A.70° B.110° C.80° D.100°
5.如图,中,于点于点与交于点,则的度数为( )
A. B. C. D.
6.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,两条对角线长的和为22cm,CD的长为5cm,则的周长为( )
A.11cm B.16cm C.27cm D.22cm
7.如图,在平行四边形ABCD中,AE平分交BC边于点E,若平行四边形ABCD的周长是28,,则AB的长为( )
A.4 B.5 C.5.5 D.6
8.在□ABCD中,∠A:∠B=7:2,则∠C等于( )
A.40° B.80° C.120° D.140°
9.在中,如果, 那么等于( )
A. B. C. D.
10.如图,已知等边△ABC的周长是12,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC则PD+PE+PF的值是( )
A.12 B.8 C.4 D.3
二、填空题
11.如图所示,在ABCD中,∠A=50°,则∠B=________,∠C=_________.
12.如图,在 ABCD中,,则∠C的度数为________.
13.在平行四边形ABCD中,∠A+∠C=240°,则∠B=______°.
14.在中,,,则的周长是______.
15.如图,在中,的垂直平分线交于点,则的周长是___________.
三、解答题
16. ABCD中,E、F在AC上,四边形DEBF是平行四边形.求证:AE=CF.
17.图①、图②、图③、图④都是的正方形网格,每个小正方形的边长均为1,每个小正方形顶点叫做格点.图①中的△ABC的顶点都在格点上.
(1)沿BC边上的高将其剪成两个三角形,用这两个三角形在图②、图③、图④中各拼成一个平行四边形,所拼得的三个平行四边形不能够完全重合.
(2)直接写出所拼得的平行四边形较长的对角线的长.
18.如图,四边形是平行四边形,、是对角线上的点,.
(1)求证:;
(2)求证:.
参考答案
1.D
【详解】∵四边形ABCD是平行四边形,
∴∠A+∠B=180°
∵∠A=154°
∴∠B=26°.
故选:D.
2.D
【详解】∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC,
∵OM⊥AC,
∴AM=CM,
∵△CDM的周长是40cm,
即:DM+CM+CD=DM+AM+CD=AD+CD=40cm,
∴平行四边形ABCD的周长为:2(AD+CD)=2×40=80(cm).
∴平行四边形ABCD的周长为80cm.
故选D.
3.C
【详解】解:∵点B的坐标为(0,2),将该三角形沿x轴向右平移得到Rt△O′A′B′,此时点B′的坐标为(2,2),
∴AA′=BB′=2,
∵△OAB是等腰直角三角形,
∴A(,),
∴AA′对应的高为,
∴线段OA在平移过程中扫过部分的图形面积为2×=4.
故选C.
4.B
【详解】解:∵四边形ABCD是平行四边形,
∴∠B=∠ADC=70°,
∵∠ADC+∠1=180°,
∴∠1=110°,
故选:B.
5.C
【详解】解:∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,
∵∠ADC=125°,
∴∠ABC=125°,
∵BE⊥DC,DF⊥BC,CD∥AB,
∴∠BED=90°,∠HFB=90°,∠BED+∠EBA=180°,
∴∠EBA=90°,
∴∠HBF=∠ABC-∠EBA=35°,
∴∠BHF=90°-∠HBF=55°,
故选:C.
6.B
【详解】解:∵四边形ABCD是平行四边形,
∴AO=OC=AC,BO=OD=BD,
∵AC+BD=22(cm),
∴CO+DO=11(cm),
∵CD=5cm,
∴△OCD的周长是CO+DO+CD=16(cm).
故选:B.
7.D
【详解】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,AD=BC,
∴∠DAE=∠AEB,
∵AE平分∠DAB,
∴∠DAE=∠EAB,
∴∠AEB=∠EAB,
∴BE=AB,
∵BC-BE=EC,
∴BC-AB=2①,
∵平行四边形ABCD的周长是28,
∴AB+BC=14②,
①+②得:2BC=12,
∴BC=8,
∴AB=6,
故选:D.
8.A
【详解】根据题意作图如下:
因为BCD是平行四边形,所以AD∥BC,AB∥CD;因为AD∥BC,所以∠A是∠B的同
的同旁内角,即∠A+∠B=180°;又因为∠A:∠B=7:2,所以可得∠A==140°;又因为AB∥CD,所以∠C是∠A的同旁内角,所以∠C=180°-140°=40°.故选择A.
9.B
【详解】解:如图,
∵四边形ABCD是平行四边形,
∴ADBC,ABCD
∴∠A+∠B=180°,∠A+∠D=180°
∵∠A=2∠B,
∴∠A=120°,
∴∠B=∠D=60°
故选:B.
10.C
【详解】作FG∥BC交 AC于G,作HE∥BC交AB于H,则△FHP、△AFG是等边三角形,四边形FGPE、四边形HBDP是平行四边形.
由图可得AF=FG=PE,FP=FH,PD=HB,
∴PD+PE+PF=HB+AF+FH=AB=12÷3=4.
故选C.
11.
【详解】解: ∵ABCD,∠A=50°,
∴∠B=130°,∠C=50°.
12.
【详解】解:∵四边形ABCD为平行四边形,
∴.
故答案为60°.
13.
【详解】解:在 ABCD中,∠A=∠C,
∵∠A+∠C=240°,
∴∠A=∠C=120°
∴∠B=180° ∠A=180° 120°=60°.
故答案为:60.
14.
【详解】解:如图:
平行四边形的周长为:.
故答案是:10.
15.
【详解】解:∵AC的垂直平分线交AD于E,
∴AE=CE,
∵四边形ABCD是平行四边形,
∴CD=AB=3,AD=BC=5,
∴△CDE的周长是:DE+CD+CE=CD+DE+AE=CD+AD=3+5=8.
故答案为:8.
16.
【详解】证明:如图,连接BD,交AC于点O.
∵四边形ABCD是平行四边形,四边形DEBF是平行四边形,
∴OA=OC,OE=OF,
∴OA-OE=OC-OF,
∴AE=CF.
17.
【详解】(1)如图.答案不唯一,以下答案供参考.
(2)所拼得的平行四边形较长的对角线的长依次是、、.
18.
【详解】证明:(1)∵四边形是平行四边形
∴,,
∴,
又,
∴.
(2)由(1)知,
∴,,
又,,
∴,
∴,
∴四边形是平行四边形,
∴.
一、单选题
1.如图,已知在□ABCD中,∠A=154°,则∠B等于( )
A.154° B.46° C.36° D.26°
2.如图,□ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M,如果△CDM的周长是40cm,则平行四边形ABCD的周长是( )
A.40cm B.60cm C.70cm D.80cm
3.如图,O为坐标原点,△OAB是等腰直角三角形,∠OAB=90°,点B的坐标为(0,2),将该三角形沿x轴向右平移得到Rt△O′A′B′,此时点B′的坐标为(2,2),则线段OA在平移过程中扫过部分的图形面积为( )
A.2 B. C.4 D.
4.如图,在平行四边形ABCD中,∠B=70°,延长CD到点E,则∠1的度数为( )
A.70° B.110° C.80° D.100°
5.如图,中,于点于点与交于点,则的度数为( )
A. B. C. D.
6.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,两条对角线长的和为22cm,CD的长为5cm,则的周长为( )
A.11cm B.16cm C.27cm D.22cm
7.如图,在平行四边形ABCD中,AE平分交BC边于点E,若平行四边形ABCD的周长是28,,则AB的长为( )
A.4 B.5 C.5.5 D.6
8.在□ABCD中,∠A:∠B=7:2,则∠C等于( )
A.40° B.80° C.120° D.140°
9.在中,如果, 那么等于( )
A. B. C. D.
10.如图,已知等边△ABC的周长是12,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC则PD+PE+PF的值是( )
A.12 B.8 C.4 D.3
二、填空题
11.如图所示,在ABCD中,∠A=50°,则∠B=________,∠C=_________.
12.如图,在 ABCD中,,则∠C的度数为________.
13.在平行四边形ABCD中,∠A+∠C=240°,则∠B=______°.
14.在中,,,则的周长是______.
15.如图,在中,的垂直平分线交于点,则的周长是___________.
三、解答题
16. ABCD中,E、F在AC上,四边形DEBF是平行四边形.求证:AE=CF.
17.图①、图②、图③、图④都是的正方形网格,每个小正方形的边长均为1,每个小正方形顶点叫做格点.图①中的△ABC的顶点都在格点上.
(1)沿BC边上的高将其剪成两个三角形,用这两个三角形在图②、图③、图④中各拼成一个平行四边形,所拼得的三个平行四边形不能够完全重合.
(2)直接写出所拼得的平行四边形较长的对角线的长.
18.如图,四边形是平行四边形,、是对角线上的点,.
(1)求证:;
(2)求证:.
参考答案
1.D
【详解】∵四边形ABCD是平行四边形,
∴∠A+∠B=180°
∵∠A=154°
∴∠B=26°.
故选:D.
2.D
【详解】∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC,
∵OM⊥AC,
∴AM=CM,
∵△CDM的周长是40cm,
即:DM+CM+CD=DM+AM+CD=AD+CD=40cm,
∴平行四边形ABCD的周长为:2(AD+CD)=2×40=80(cm).
∴平行四边形ABCD的周长为80cm.
故选D.
3.C
【详解】解:∵点B的坐标为(0,2),将该三角形沿x轴向右平移得到Rt△O′A′B′,此时点B′的坐标为(2,2),
∴AA′=BB′=2,
∵△OAB是等腰直角三角形,
∴A(,),
∴AA′对应的高为,
∴线段OA在平移过程中扫过部分的图形面积为2×=4.
故选C.
4.B
【详解】解:∵四边形ABCD是平行四边形,
∴∠B=∠ADC=70°,
∵∠ADC+∠1=180°,
∴∠1=110°,
故选:B.
5.C
【详解】解:∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,
∵∠ADC=125°,
∴∠ABC=125°,
∵BE⊥DC,DF⊥BC,CD∥AB,
∴∠BED=90°,∠HFB=90°,∠BED+∠EBA=180°,
∴∠EBA=90°,
∴∠HBF=∠ABC-∠EBA=35°,
∴∠BHF=90°-∠HBF=55°,
故选:C.
6.B
【详解】解:∵四边形ABCD是平行四边形,
∴AO=OC=AC,BO=OD=BD,
∵AC+BD=22(cm),
∴CO+DO=11(cm),
∵CD=5cm,
∴△OCD的周长是CO+DO+CD=16(cm).
故选:B.
7.D
【详解】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,AD=BC,
∴∠DAE=∠AEB,
∵AE平分∠DAB,
∴∠DAE=∠EAB,
∴∠AEB=∠EAB,
∴BE=AB,
∵BC-BE=EC,
∴BC-AB=2①,
∵平行四边形ABCD的周长是28,
∴AB+BC=14②,
①+②得:2BC=12,
∴BC=8,
∴AB=6,
故选:D.
8.A
【详解】根据题意作图如下:
因为BCD是平行四边形,所以AD∥BC,AB∥CD;因为AD∥BC,所以∠A是∠B的同
的同旁内角,即∠A+∠B=180°;又因为∠A:∠B=7:2,所以可得∠A==140°;又因为AB∥CD,所以∠C是∠A的同旁内角,所以∠C=180°-140°=40°.故选择A.
9.B
【详解】解:如图,
∵四边形ABCD是平行四边形,
∴ADBC,ABCD
∴∠A+∠B=180°,∠A+∠D=180°
∵∠A=2∠B,
∴∠A=120°,
∴∠B=∠D=60°
故选:B.
10.C
【详解】作FG∥BC交 AC于G,作HE∥BC交AB于H,则△FHP、△AFG是等边三角形,四边形FGPE、四边形HBDP是平行四边形.
由图可得AF=FG=PE,FP=FH,PD=HB,
∴PD+PE+PF=HB+AF+FH=AB=12÷3=4.
故选C.
11.
【详解】解: ∵ABCD,∠A=50°,
∴∠B=130°,∠C=50°.
12.
【详解】解:∵四边形ABCD为平行四边形,
∴.
故答案为60°.
13.
【详解】解:在 ABCD中,∠A=∠C,
∵∠A+∠C=240°,
∴∠A=∠C=120°
∴∠B=180° ∠A=180° 120°=60°.
故答案为:60.
14.
【详解】解:如图:
平行四边形的周长为:.
故答案是:10.
15.
【详解】解:∵AC的垂直平分线交AD于E,
∴AE=CE,
∵四边形ABCD是平行四边形,
∴CD=AB=3,AD=BC=5,
∴△CDE的周长是:DE+CD+CE=CD+DE+AE=CD+AD=3+5=8.
故答案为:8.
16.
【详解】证明:如图,连接BD,交AC于点O.
∵四边形ABCD是平行四边形,四边形DEBF是平行四边形,
∴OA=OC,OE=OF,
∴OA-OE=OC-OF,
∴AE=CF.
17.
【详解】(1)如图.答案不唯一,以下答案供参考.
(2)所拼得的平行四边形较长的对角线的长依次是、、.
18.
【详解】证明:(1)∵四边形是平行四边形
∴,,
∴,
又,
∴.
(2)由(1)知,
∴,,
又,,
∴,
∴,
∴四边形是平行四边形,
∴.
