人教版八年级下册数学24.1.4圆周角 课件(共22张PPT)
文档属性
| 名称 | 人教版八年级下册数学24.1.4圆周角 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 17.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 16:19:25 | ||
图片预览



文档简介
(共22张PPT)
圆周角
24.1.4
(第一课时)
学习目标
1、理解圆周角的概念,会叙述并证明圆周角定理;
学习目标
2、理解同弧所对的圆周角与圆心角的关系,并能运用圆周角定理解决简单的几何问题。
B
C
A
A1
A2
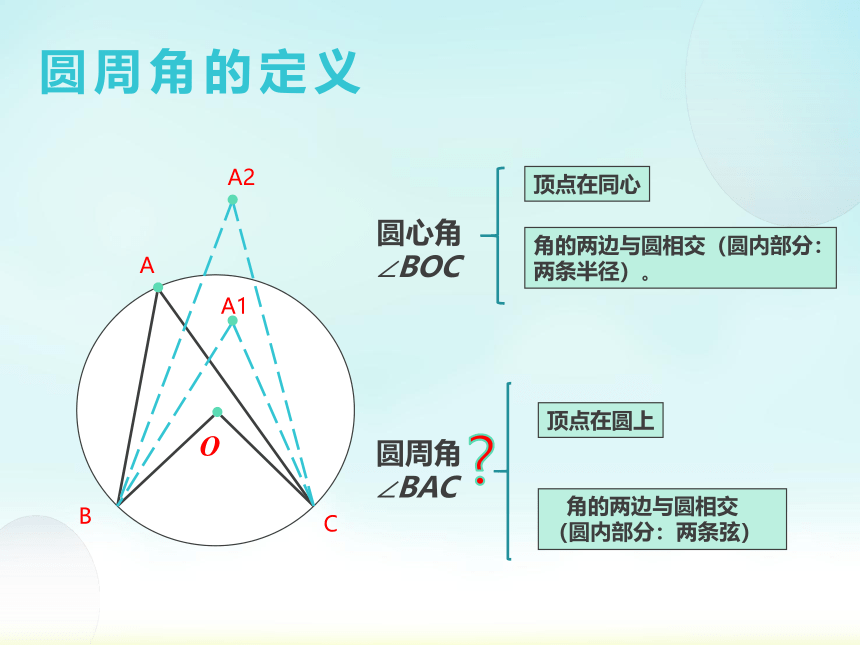
圆周角的定义
圆心角
∠BOC
角的两边与圆相交(圆内部分:两条半径)。
圆周角
∠BAC
角的两边与圆相交
(圆内部分:两条弦)
顶点在同心
顶点在圆上
O
·
C
O
B
·
C
O
B
A
·
C
O
A
B
(1)
(2)
(3)
·
C
O
B
A
(4)
(5)
(6)
·
C
O
A
·
O
A
B
C
B
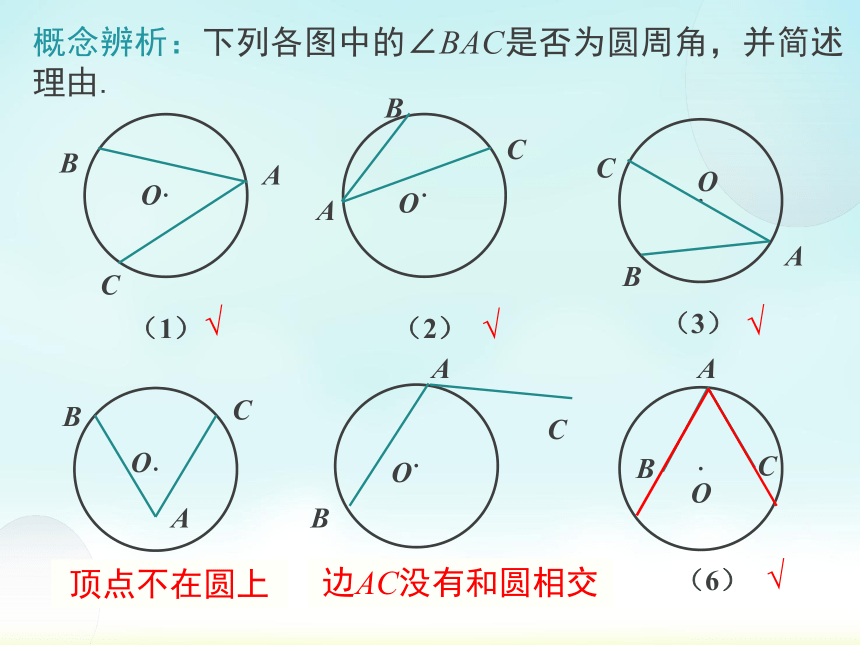
概念辨析:下列各图中的∠BAC是否为圆周角,并简述理由.
√
√
√
顶点不在圆上
边AC没有和圆相交
√
A
C
A
B
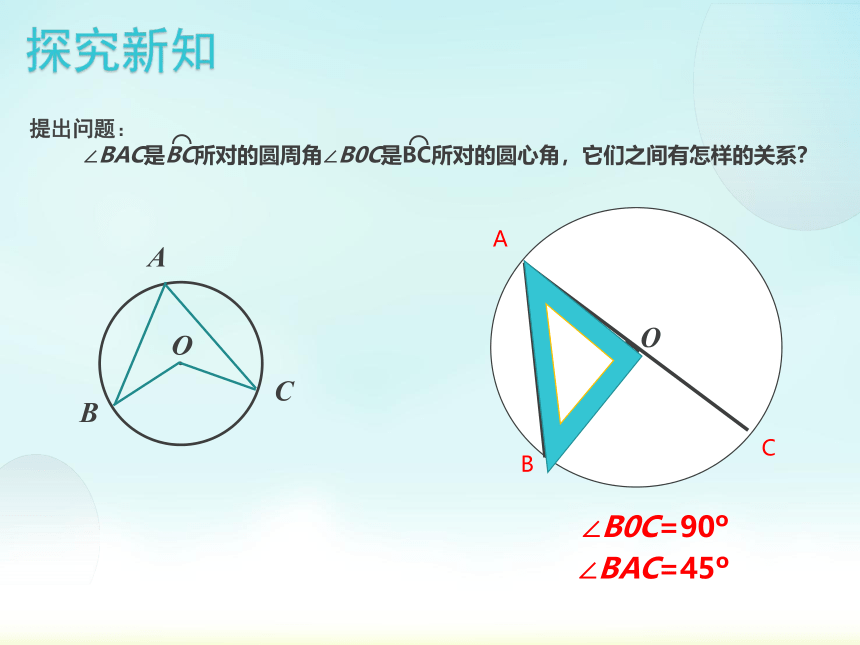
探究新知
提出问题:
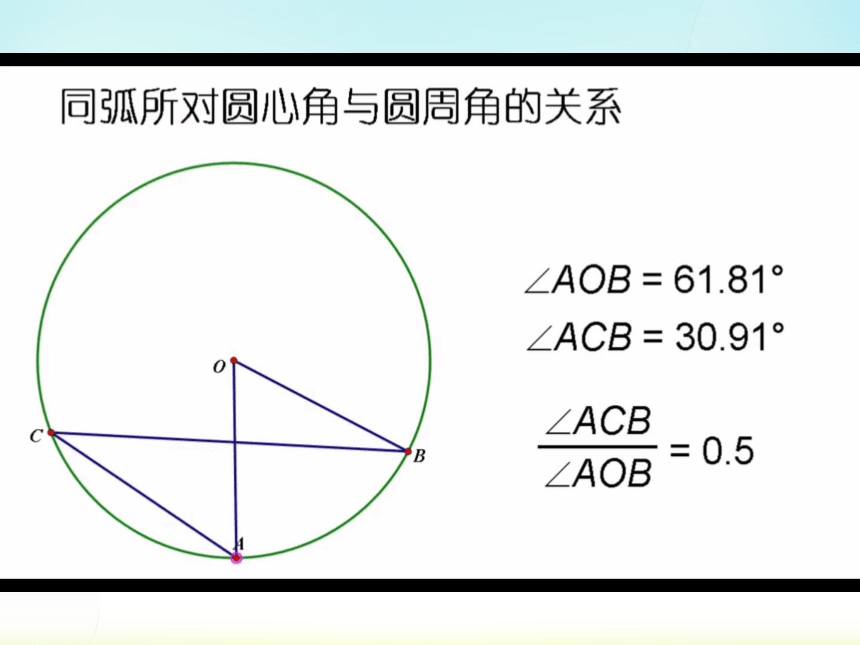
∠BAC是BC所对的圆周角∠B0C是BC所对的圆心角,它们之间有怎样的关系?
⌒
⌒
·
A
O
B
C
∠BAC=45
∠B0C=90
O
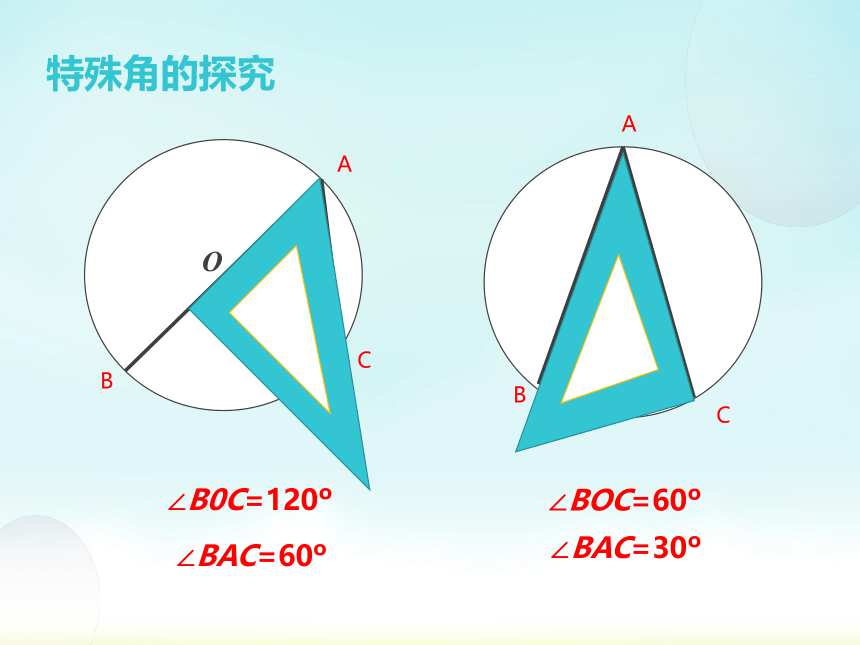
特殊角的探究
O
B
A
C
∠BOC=60
A
B
∠B0C=120
∠BAC=60
∠BAC=30
C
C
O
学生活动
一般角的探究: 画一画、量一量
几何画板演示
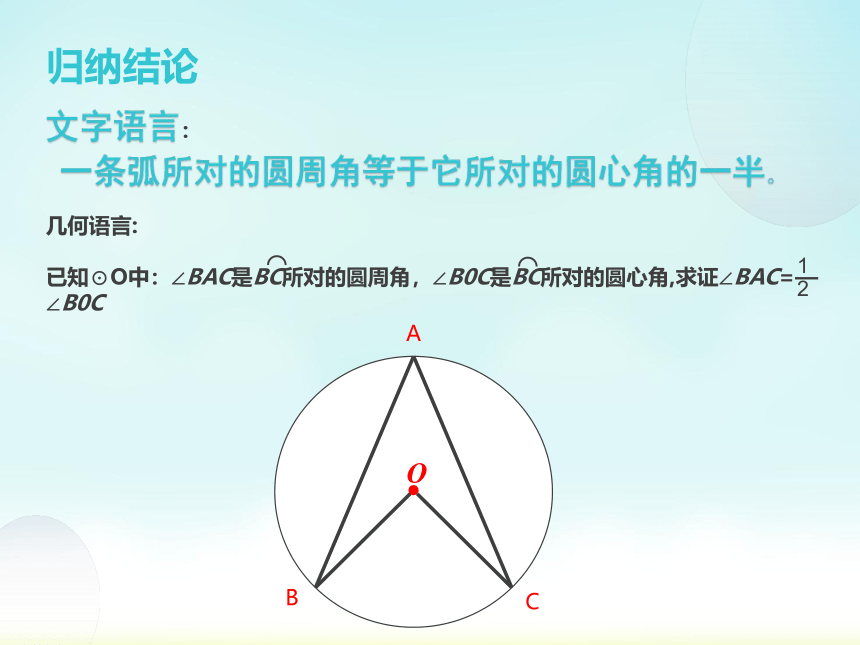
归纳结论
几何语言:
已知⊙O中:∠BAC是BC所对的圆周角,∠B0C是BC所对的圆心角,求证∠BAC=— ∠B0C
⌒
⌒
1
2
文字语言:
B
A
C
一条弧所对的圆周角等于它所对的圆心角的一半。
O
推理验证
B
C
A
A
A
观察思考:
问题一: 一条弧所对的圆周角有多少个?
问题二:一条弧所对的圆周角与圆心的位置关系有几种?
A
O
圆心O在∠BAC的内部
圆心O在
∠BAC的一边上
圆心O在
∠BAC的外部
圆心O与圆周角的位置有以下三种情况,我们一一讨论.
分类讨论
圆心O在∠BAC的一边上(特殊情形)
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
当圆心在圆周角内部时,如何证明∠BAC= ∠BOC.
合作探究
O
A
B
D
O
A
C
D
O
A
B
C
D
圆心O在∠BAC的内部
O
A
C
D
O
A
B
D
合作探究2
当圆心在圆周角外部时,如何证明∠BAC= ∠BOC.
O
A
B
D
C
O
A
D
C
O
A
B
D
C
O
A
D
O
A
B
D
C
O
A
D
O
A
B
D
圆心O在∠BAC的外部
一条弧所对的圆周角等于它所对的圆心角的一半。
圆周角定理
∵BC=BC
∴∠BAC= ∠BOC.
⌒
⌒
文字语言:
几何语言:
·
·
·
100
A
O
20°
O
90°
A
B
A
B
B
C
C
(1)
(2)
(3)
求∠AOB
求∠AOB
求∠A
练一练
O
°·
·
·
100
A
O
20°
O
90°
A
B
A
B
B
C
C
(1)
(2)
(3)
求∠AOB
求∠AOB
求∠A
练一练
课堂小结
同学们:
1、本节课学会了哪些数学知识?
2、我们是如何证明圆周角定理的?在证明过程中用到了哪些思想方法?
归纳总结:
圆周角定义 圆周角定理
分类
转化
推理
A
B
D
C
从特殊到一般
A
D
B
C
A
C
B
O
O
O
再见!
圆周角
24.1.4
(第一课时)
学习目标
1、理解圆周角的概念,会叙述并证明圆周角定理;
学习目标
2、理解同弧所对的圆周角与圆心角的关系,并能运用圆周角定理解决简单的几何问题。
B
C
A
A1
A2
圆周角的定义
圆心角
∠BOC
角的两边与圆相交(圆内部分:两条半径)。
圆周角
∠BAC
角的两边与圆相交
(圆内部分:两条弦)
顶点在同心
顶点在圆上
O
·
C
O
B
·
C
O
B
A
·
C
O
A
B
(1)
(2)
(3)
·
C
O
B
A
(4)
(5)
(6)
·
C
O
A
·
O
A
B
C
B
概念辨析:下列各图中的∠BAC是否为圆周角,并简述理由.
√
√
√
顶点不在圆上
边AC没有和圆相交
√
A
C
A
B
探究新知
提出问题:
∠BAC是BC所对的圆周角∠B0C是BC所对的圆心角,它们之间有怎样的关系?
⌒
⌒
·
A
O
B
C
∠BAC=45
∠B0C=90
O
特殊角的探究
O
B
A
C
∠BOC=60
A
B
∠B0C=120
∠BAC=60
∠BAC=30
C
C
O
学生活动
一般角的探究: 画一画、量一量
几何画板演示
归纳结论
几何语言:
已知⊙O中:∠BAC是BC所对的圆周角,∠B0C是BC所对的圆心角,求证∠BAC=— ∠B0C
⌒
⌒
1
2
文字语言:
B
A
C
一条弧所对的圆周角等于它所对的圆心角的一半。
O
推理验证
B
C
A
A
A
观察思考:
问题一: 一条弧所对的圆周角有多少个?
问题二:一条弧所对的圆周角与圆心的位置关系有几种?
A
O
圆心O在∠BAC的内部
圆心O在
∠BAC的一边上
圆心O在
∠BAC的外部
圆心O与圆周角的位置有以下三种情况,我们一一讨论.
分类讨论
圆心O在∠BAC的一边上(特殊情形)
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
当圆心在圆周角内部时,如何证明∠BAC= ∠BOC.
合作探究
O
A
B
D
O
A
C
D
O
A
B
C
D
圆心O在∠BAC的内部
O
A
C
D
O
A
B
D
合作探究2
当圆心在圆周角外部时,如何证明∠BAC= ∠BOC.
O
A
B
D
C
O
A
D
C
O
A
B
D
C
O
A
D
O
A
B
D
C
O
A
D
O
A
B
D
圆心O在∠BAC的外部
一条弧所对的圆周角等于它所对的圆心角的一半。
圆周角定理
∵BC=BC
∴∠BAC= ∠BOC.
⌒
⌒
文字语言:
几何语言:
·
·
·
100
A
O
20°
O
90°
A
B
A
B
B
C
C
(1)
(2)
(3)
求∠AOB
求∠AOB
求∠A
练一练
O
°·
·
·
100
A
O
20°
O
90°
A
B
A
B
B
C
C
(1)
(2)
(3)
求∠AOB
求∠AOB
求∠A
练一练
课堂小结
同学们:
1、本节课学会了哪些数学知识?
2、我们是如何证明圆周角定理的?在证明过程中用到了哪些思想方法?
归纳总结:
圆周角定义 圆周角定理
分类
转化
推理
A
B
D
C
从特殊到一般
A
D
B
C
A
C
B
O
O
O
再见!
同课章节目录
