人教版九年级下册数学第二十八章 锐角三角函数 数学活动(共16张PPT)
文档属性
| 名称 | 人教版九年级下册数学第二十八章 锐角三角函数 数学活动(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 16:22:28 | ||
图片预览


文档简介
(共16张PPT)
锐角三角函数 数学活动
【学习任务一】
自主预习课本第81页至第82页《数学活动》.
【学习任务二】
能够根据三角函数测高的原理制定测量方案.
【学习任务三】
能够制作测角仪并掌握测角仪测角的方法.
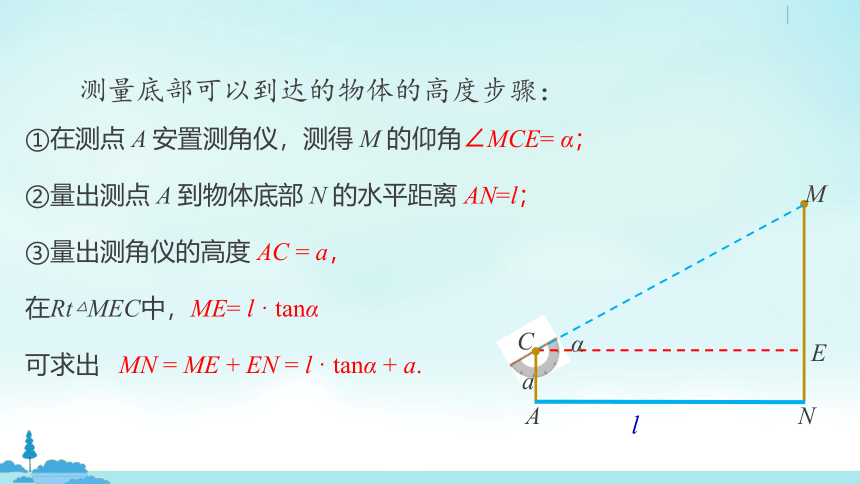
①在测点 A 安置测角仪,测得 M 的仰角∠MCE= α;
②量出测点 A 到物体底部 N 的水平距离 AN=l;
③量出测角仪的高度 AC = a,
测量底部可以到达的物体的高度步骤:
A
C
M
N
E
α
a
l
在Rt△MEC中,ME= l · tanα
可求出 MN = ME + EN = l · tanα + a.
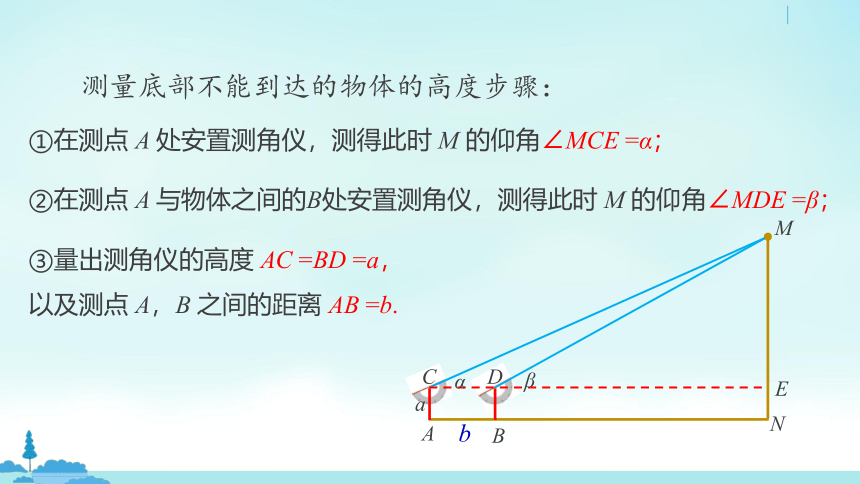
测量底部不能到达的物体的高度步骤:
①在测点 A 处安置测角仪,测得此时 M 的仰角∠MCE =α;
②在测点 A 与物体之间的B处安置测角仪,测得此时 M 的仰角∠MDE =β;
A
C
B
D
M
N
E
α
β
a
③量出测角仪的高度 AC =BD =a,
以及测点 A,B 之间的距离 AB =b.
b
A
C
B
D
M
N
E
α
β
a
b
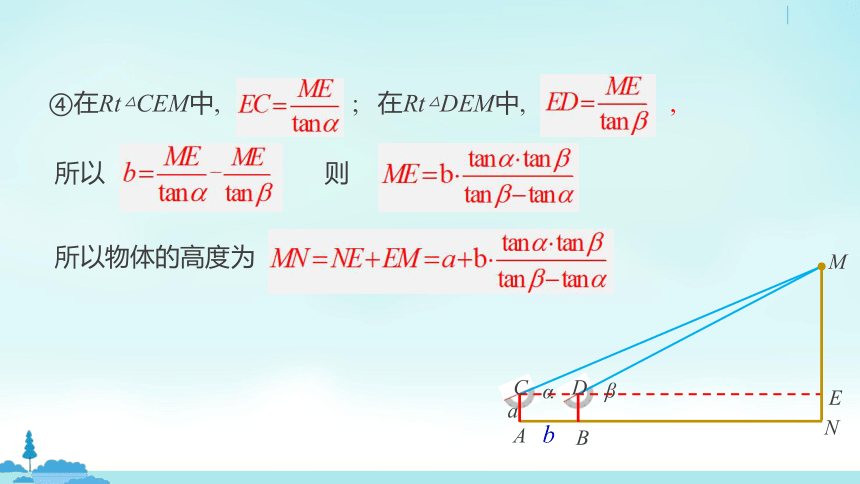
④在Rt△CEM中, ; 在Rt△DEM中, ,
所以 则
所以物体的高度为
150tanα
1.5
A
E
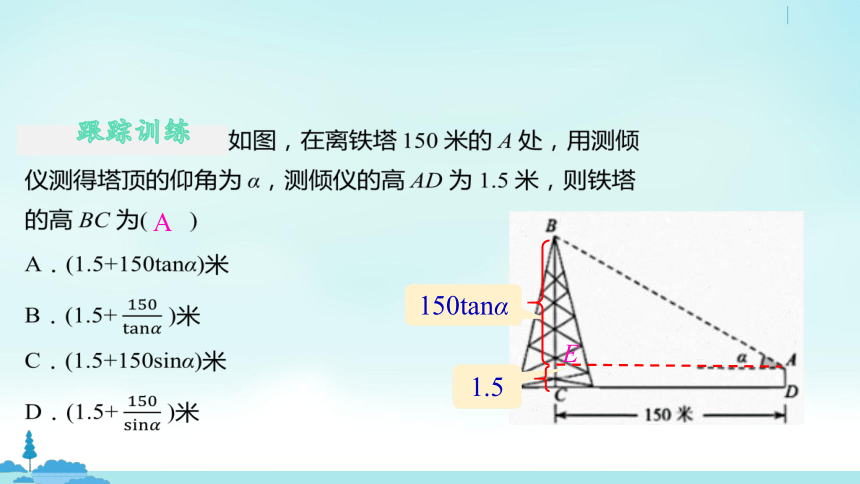
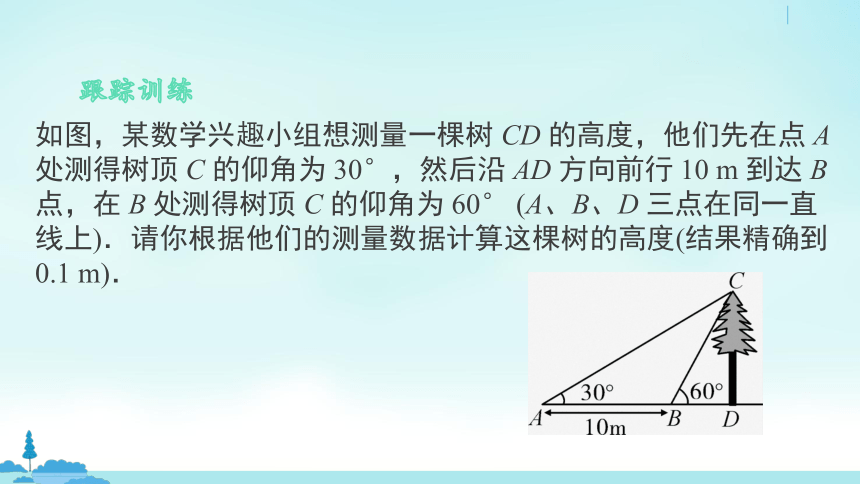
跟踪训练
如图,某数学兴趣小组想测量一棵树 CD 的高度,他们先在点 A 处测得树顶 C 的仰角为 30°,然后沿 AD 方向前行 10 m 到达 B 点,在 B 处测得树顶 C 的仰角为 60° (A、B、D 三点在同一直线上).请你根据他们的测量数据计算这棵树的高度(结果精确到 0.1 m).
跟踪训练
解:设CD=x.
针对本题你还有没有别的解法呢?
在Rt△BCD中,
在Rt△ACD中,
∵AB=AD-BD,即
即
解:∵∠A=30°∠CBD=60°
∴AB=BC=10
∴∠ACB=30°
在Rt△BCD中,
制定测量高度的方案
1、活动分组:6人一组,分工合作(组长A、器材管理员B、测量员C、记录员D、计算员E、复核员F).
2、小组根据需要测量的对象的实际情况,先讨论研究测量方案及具体的操作步骤,分别讨论底部可以到达的物体的高度(操场边的国旗)、底部不可以到达的物体的高度(教学楼顶的校牌)各需要测量哪些数据.
3、提前在活动报告上画好示意图,为开展测量活动做好准备.
活
动
报
告
把一根细线固定在半圆形量角器的圆心处,在细线的另一端系一个小重物,制成一个简单的测角仪,利用它可以测量仰角或俯角。
如何使用测角仪呢?
将仪器用手托起,拿到眼前,使视线沿着仪器的直径刚好到达树的最高点(如图).
α = 90°-∠ABC
α = ∠ABC - 90°
测角仪上角的读数与仰角有怎样的关系?
测角仪上角的读数与俯角有怎样的关系?
课后作业
课后完成测角仪制作,小组合作完成标的物的测量,
完成活动报告的填写.
同学们行动起来吧!
锐角三角函数 数学活动
【学习任务一】
自主预习课本第81页至第82页《数学活动》.
【学习任务二】
能够根据三角函数测高的原理制定测量方案.
【学习任务三】
能够制作测角仪并掌握测角仪测角的方法.
①在测点 A 安置测角仪,测得 M 的仰角∠MCE= α;
②量出测点 A 到物体底部 N 的水平距离 AN=l;
③量出测角仪的高度 AC = a,
测量底部可以到达的物体的高度步骤:
A
C
M
N
E
α
a
l
在Rt△MEC中,ME= l · tanα
可求出 MN = ME + EN = l · tanα + a.
测量底部不能到达的物体的高度步骤:
①在测点 A 处安置测角仪,测得此时 M 的仰角∠MCE =α;
②在测点 A 与物体之间的B处安置测角仪,测得此时 M 的仰角∠MDE =β;
A
C
B
D
M
N
E
α
β
a
③量出测角仪的高度 AC =BD =a,
以及测点 A,B 之间的距离 AB =b.
b
A
C
B
D
M
N
E
α
β
a
b
④在Rt△CEM中, ; 在Rt△DEM中, ,
所以 则
所以物体的高度为
150tanα
1.5
A
E
跟踪训练
如图,某数学兴趣小组想测量一棵树 CD 的高度,他们先在点 A 处测得树顶 C 的仰角为 30°,然后沿 AD 方向前行 10 m 到达 B 点,在 B 处测得树顶 C 的仰角为 60° (A、B、D 三点在同一直线上).请你根据他们的测量数据计算这棵树的高度(结果精确到 0.1 m).
跟踪训练
解:设CD=x.
针对本题你还有没有别的解法呢?
在Rt△BCD中,
在Rt△ACD中,
∵AB=AD-BD,即
即
解:∵∠A=30°∠CBD=60°
∴AB=BC=10
∴∠ACB=30°
在Rt△BCD中,
制定测量高度的方案
1、活动分组:6人一组,分工合作(组长A、器材管理员B、测量员C、记录员D、计算员E、复核员F).
2、小组根据需要测量的对象的实际情况,先讨论研究测量方案及具体的操作步骤,分别讨论底部可以到达的物体的高度(操场边的国旗)、底部不可以到达的物体的高度(教学楼顶的校牌)各需要测量哪些数据.
3、提前在活动报告上画好示意图,为开展测量活动做好准备.
活
动
报
告
把一根细线固定在半圆形量角器的圆心处,在细线的另一端系一个小重物,制成一个简单的测角仪,利用它可以测量仰角或俯角。
如何使用测角仪呢?
将仪器用手托起,拿到眼前,使视线沿着仪器的直径刚好到达树的最高点(如图).
α = 90°-∠ABC
α = ∠ABC - 90°
测角仪上角的读数与仰角有怎样的关系?
测角仪上角的读数与俯角有怎样的关系?
课后作业
课后完成测角仪制作,小组合作完成标的物的测量,
完成活动报告的填写.
同学们行动起来吧!
