人教版八年级上册数学 13.1.2《线段垂直平分线的性质》 课件 (共19张PPT)
文档属性
| 名称 | 人教版八年级上册数学 13.1.2《线段垂直平分线的性质》 课件 (共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 19:18:20 | ||
图片预览





文档简介
(共19张PPT)
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
情境引入
得出猜想
情境引入
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
得出猜想
得出猜想
当CD垂直平分AB时,观察CA和CB、DA和DB长度的关系.
猜想:
CA=CB、DA=DB
情境引入
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
概念生成
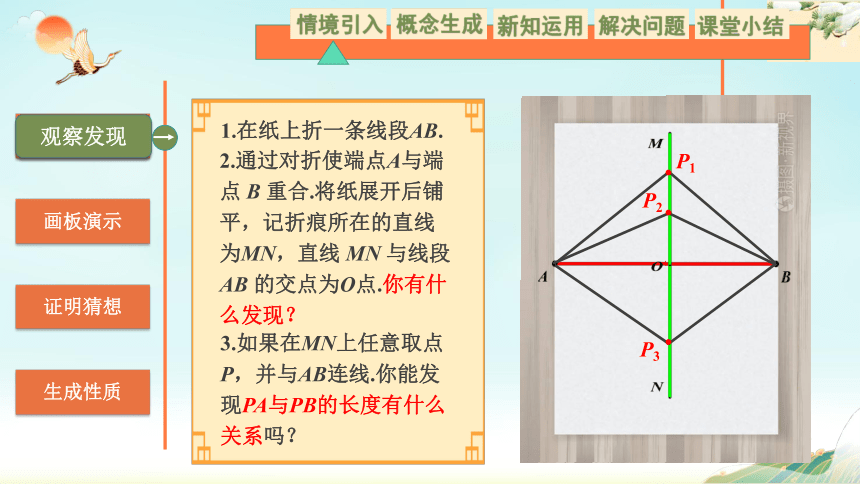
1.在纸上折一条线段AB.
2.通过对折使端点A与端点 B 重合.将纸展开后铺平,记折痕所在的直线为MN,直线 MN 与线段AB 的交点为O点.你有什么发现?
3.如果在MN上任意取点P,并与AB连线.你能发现PA与PB的长度有什么关系吗?
.
.
.
P1
P2
P3
观察发现
画板演示
证明猜想
生成性质
观察发现
观察发现
画板演示
证明猜想
生成性质
观察发现
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
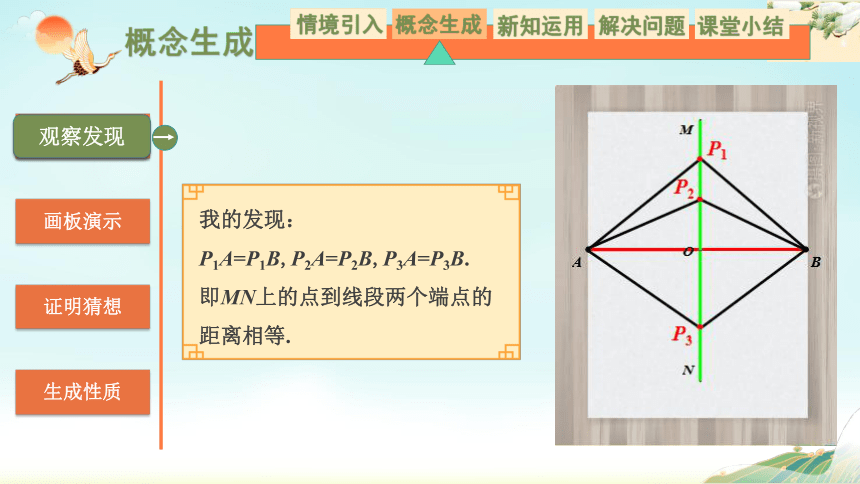
我的发现:P1A=P1B,P2A=P2B,P3A=P3B.
即MN上的点到线段两个端点的距离相等.
概念生成
观察发现
画板演示
证明猜想
性质生成
画板演示
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
概念生成
START
观察发现
画板演示
证明猜想
性质生成
证明猜想
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
概念生成
已知:如图,直线MN⊥AB,垂足为O,AO =OB,点P 在MN上.
求证:PA =PB.
O
A
B
P
M
N
证明猜想:垂直平分线上的点到线段两端点距离相等
观察发现
画板演示
证明猜想
性质生成
证明猜想
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
概念生成
证明:∵MN⊥AB,
∴∠POA=∠POB.
又∵AO=BO,PO=PO,
∴△POA≌△POB(SAS)
∴PA=PB.
A
B
P
O
M
N
证明猜想:垂直平分线上的点到线段两端点距离相等
观察发现
画板演示
证明猜想
性质生成
性质生成
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
概念生成
线段垂直平分线的性质
线段垂直平分线上的点到这条线段两个端点的距离相等.
符号语言
∵ MN⊥AB,AO=BO,
∴ PA=PB.
巩固练习1
巩固练习1
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
概念生成
1.如图,CD是AB的垂直平分线,若AC=1.5 cm,BD=2.5 cm,则四边形ACBD的周长为 cm.
8
巩固练习3
巩固练习2
巩固练习1
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
概念生成
巩固练习3
巩固练习2
2.如图,在△ABC中,AB=AC=20 cm,DE垂直平分AB,垂足为E,交AC于点D,若△DBC的周长为35 cm,则BC的长为 ( )
A.5 cm B.10 cm
C.15 cm D.17.5 cm
C
巩固练习2
巩固练习1
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
概念生成
巩固练习3
巩固练习3
巩固练习2
3.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC, AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( )
A.50° B.70° C.75° D.80°
B
观察发现
得出猜想
画板演示
证明猜想
证明猜想
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
概念生成
已知:如图,直线MN⊥AB,垂足为O,PA =PB.
求证:点P 在线段AB 的垂直平分线上.
P
A
B
O
M
N
猜想:到线段两端点距离相等的点在线段的垂直平分线上.
证明:∵MN⊥AB,
∴∠POA=∠POB.
又∵PA=PB,PO=PO,
∴△POA≌△POB(HL)
∴OA=OB,即MN平分线段AB.
∴点P 在线段AB 的垂直平分线上.
观察发现
得出猜想
画板演示
证明猜想
证明猜想
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
概念生成
线段垂直平分线的判定
与线段两个端点距离相等的点在这条线段的垂直平分线上.
符号语言
∵PA=PB,
∴点P 在线段AB 的垂直平分线上
解决问题
课堂小结
情境引入
情境引入
概念生成
新知运用
新知运用
尺规作图:利用线段垂直平分线的判定,过已知直线外一点,作已知直线的垂线.
例题.如图,已知直线AB和直线外一点C,求作直线 AB的垂线,使垂线经过C点.
合作探究
成果展示
合作探究
解决问题
课堂小结
情境引入
情境引入
概念生成
新知运用
解决问题
合作探究:某地开发商为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个快递驿站P,试问该快递驿站应建于何处,才能使得它到三个小区的距离相等?
B
C
A
合作探究
成果展示
成果展示
解决问题
课堂小结
情境引入
情境引入
概念生成
新知运用
解决问题
解决问题
C
B
A
.
.
.
.
P
解决问题
课堂小结
情境引入
情境引入
概念生成
新知运用
课堂小结
性质
垂直平分线上的点与线段两个端点的距离相等.
线段的垂直平分线
判定
与线段两端点距离相等的点在线段的垂直平分线上.
尺规
作图
过直线外一点作已知直线的垂线.
祝同学们:
学习进步,天天向上!
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
情境引入
得出猜想
情境引入
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
得出猜想
得出猜想
当CD垂直平分AB时,观察CA和CB、DA和DB长度的关系.
猜想:
CA=CB、DA=DB
情境引入
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
概念生成
1.在纸上折一条线段AB.
2.通过对折使端点A与端点 B 重合.将纸展开后铺平,记折痕所在的直线为MN,直线 MN 与线段AB 的交点为O点.你有什么发现?
3.如果在MN上任意取点P,并与AB连线.你能发现PA与PB的长度有什么关系吗?
.
.
.
P1
P2
P3
观察发现
画板演示
证明猜想
生成性质
观察发现
观察发现
画板演示
证明猜想
生成性质
观察发现
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
我的发现:P1A=P1B,P2A=P2B,P3A=P3B.
即MN上的点到线段两个端点的距离相等.
概念生成
观察发现
画板演示
证明猜想
性质生成
画板演示
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
概念生成
START
观察发现
画板演示
证明猜想
性质生成
证明猜想
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
概念生成
已知:如图,直线MN⊥AB,垂足为O,AO =OB,点P 在MN上.
求证:PA =PB.
O
A
B
P
M
N
证明猜想:垂直平分线上的点到线段两端点距离相等
观察发现
画板演示
证明猜想
性质生成
证明猜想
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
概念生成
证明:∵MN⊥AB,
∴∠POA=∠POB.
又∵AO=BO,PO=PO,
∴△POA≌△POB(SAS)
∴PA=PB.
A
B
P
O
M
N
证明猜想:垂直平分线上的点到线段两端点距离相等
观察发现
画板演示
证明猜想
性质生成
性质生成
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
概念生成
线段垂直平分线的性质
线段垂直平分线上的点到这条线段两个端点的距离相等.
符号语言
∵ MN⊥AB,AO=BO,
∴ PA=PB.
巩固练习1
巩固练习1
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
概念生成
1.如图,CD是AB的垂直平分线,若AC=1.5 cm,BD=2.5 cm,则四边形ACBD的周长为 cm.
8
巩固练习3
巩固练习2
巩固练习1
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
概念生成
巩固练习3
巩固练习2
2.如图,在△ABC中,AB=AC=20 cm,DE垂直平分AB,垂足为E,交AC于点D,若△DBC的周长为35 cm,则BC的长为 ( )
A.5 cm B.10 cm
C.15 cm D.17.5 cm
C
巩固练习2
巩固练习1
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
概念生成
巩固练习3
巩固练习3
巩固练习2
3.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC, AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( )
A.50° B.70° C.75° D.80°
B
观察发现
得出猜想
画板演示
证明猜想
证明猜想
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
概念生成
已知:如图,直线MN⊥AB,垂足为O,PA =PB.
求证:点P 在线段AB 的垂直平分线上.
P
A
B
O
M
N
猜想:到线段两端点距离相等的点在线段的垂直平分线上.
证明:∵MN⊥AB,
∴∠POA=∠POB.
又∵PA=PB,PO=PO,
∴△POA≌△POB(HL)
∴OA=OB,即MN平分线段AB.
∴点P 在线段AB 的垂直平分线上.
观察发现
得出猜想
画板演示
证明猜想
证明猜想
概念生成
新知运用
解决问题
课堂小结
情境引入
情境引入
概念生成
线段垂直平分线的判定
与线段两个端点距离相等的点在这条线段的垂直平分线上.
符号语言
∵PA=PB,
∴点P 在线段AB 的垂直平分线上
解决问题
课堂小结
情境引入
情境引入
概念生成
新知运用
新知运用
尺规作图:利用线段垂直平分线的判定,过已知直线外一点,作已知直线的垂线.
例题.如图,已知直线AB和直线外一点C,求作直线 AB的垂线,使垂线经过C点.
合作探究
成果展示
合作探究
解决问题
课堂小结
情境引入
情境引入
概念生成
新知运用
解决问题
合作探究:某地开发商为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个快递驿站P,试问该快递驿站应建于何处,才能使得它到三个小区的距离相等?
B
C
A
合作探究
成果展示
成果展示
解决问题
课堂小结
情境引入
情境引入
概念生成
新知运用
解决问题
解决问题
C
B
A
.
.
.
.
P
解决问题
课堂小结
情境引入
情境引入
概念生成
新知运用
课堂小结
性质
垂直平分线上的点与线段两个端点的距离相等.
线段的垂直平分线
判定
与线段两端点距离相等的点在线段的垂直平分线上.
尺规
作图
过直线外一点作已知直线的垂线.
祝同学们:
学习进步,天天向上!
