8.2.2 弹性势能 课件 (共15张PPT) 高一下学期物理人教版(2019)必修第二册
文档属性
| 名称 | 8.2.2 弹性势能 课件 (共15张PPT) 高一下学期物理人教版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 14.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-03-21 21:28:03 | ||
图片预览





文档简介
(共15张PPT)
§8.22 弹性势能
第八章 机械能守恒定律
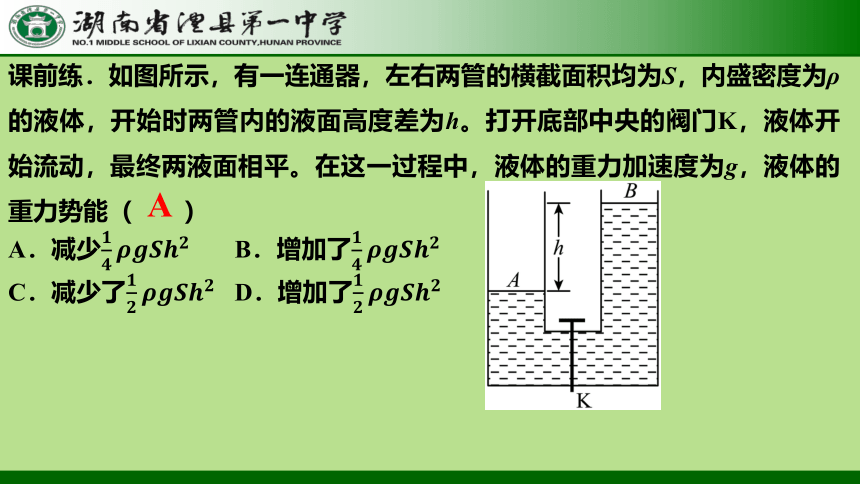
课前练.如图所示,有一连通器,左右两管的横截面积均为S,内盛密度为ρ的液体,开始时两管内的液面高度差为h。打开底部中央的阀门K,液体开始流动,最终两液面相平。在这一过程中,液体的重力加速度为g,液体的重力势能( )
A.减少 B.增加了
C.减少了 D.增加了
A
知识回顾
一、重力做的功
WG = mgh (h为高度差)
1. 表达式
2. 特点
物体运动时, 重力对它做的功只跟它的起点和终点的位置有关,而跟物体运动的路径无关 。
二、重力势能
EP = mgh (h为高度)
1. 表达式
2. 重力势能的系统性
3. 重力做功与重力势能变化的关系:
WG = EP1 - EP2
= - EP
4. 重力势能的相对性:
5. 绳子、链条类匀质物体重力势能的求法
一、弹性势能
1. 定义:发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫做弹性势能。
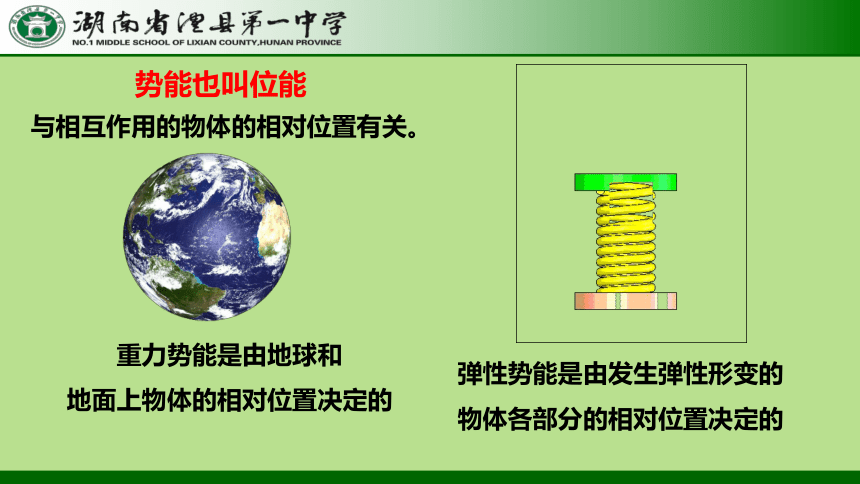
重力势能是由地球和
地面上物体的相对位置决定的
势能也叫位能
与相互作用的物体的相对位置有关。
弹性势能是由发生弹性形变的
物体各部分的相对位置决定的
2. 性质:
(1)相对性:弹簧处于原长时为零势能点。
(2)系统性:弹性势能是整个弹簧系统所具有的。
一、弹性势能
1. 定义:发生弹性形变的物体的各部分之间,由于有弹力的相互作用,
也具有势能,这种势能叫做弹性势能。
结合弹簧思考:弹性势能的大小可能与哪些因素有关?
课堂探究一:如图所示,滑块以初速度v冲向固定在竖直墙壁上的弹簧,
并将弹簧压缩.
(1)在弹簧压缩的过程中,分析弹簧弹力做功情况及弹性势能的变化;
(2)在弹簧恢复形变,从最大压缩量向原长恢复的过程中,
分析弹簧弹力做功情况及弹性势能的变化.
弹力做正功,弹性势能减小
弹力做负功,弹性势能增加
W弹 = - EP
2. 性质:
(1)相对性:弹簧处于原长时为零势能点。
(2)系统性:弹性势能是整个弹簧系统所具有的。
一、弹性势能
1. 定义:发生弹性形变的物体的各部分之间,由于有弹力的相互作用,
也具有势能,这种势能叫做弹性势能。
3. 弹力做功与弹性势能变化的关系:
W弹 = - EP
弹力做功等于弹性势能变化量的相反数
课堂探究一:如图所示,滑块以初速度v冲向固定在竖直墙壁上的弹簧,
并将弹簧压缩.
(1)在弹簧压缩的过程中,分析弹簧弹力做功情况及弹性势能的变化;
(2)在弹簧恢复形变,从最大压缩量向原长恢复的过程中,
分析弹簧弹力做功情况及弹性势能的变化.
(3)若弹簧劲度系数为k , 那么在弹簧压缩(或拉伸) x 的过程中,
求弹簧弹力做的功W弹 ?(用什么方法求?)
平均力法、图像法
2. 性质:
(1)相对性:弹簧处于原长时为零势能点。
(2)系统性:弹性势能是整个弹簧系统所具有的。
一、弹性势能
1. 定义:发生弹性形变的物体的各部分之间,由于有弹力的相互作用,
也具有势能,这种势能叫做弹性势能。
3. 弹力做功与弹性势能变化的关系:
W弹 = - EP
弹力做功等于弹性势能变化量的相反数
4. 弹性势能表达式:
EP弹 = k x2
弹簧的劲度系数
弹簧的形变量: 伸长量或压缩量
弹性势能的变化
弹力做功
重力做正功,重力势能减小
重力做负功,重力势能增加
弹力做正功,弹性势能减小
弹力做负功,弹性势能增加
W弹 = - EP
势能与力做功的关系
重力势能的变化
重力做功
WG = EP1 - EP2= - EP
[例3] (多选)关于弹性势能,下列说法正确的是( )
A.弹簧弹力做正功时,弹性势能增加
B.发生弹性形变的物体都具有弹性势能
C.弹性势能可以与其他形式的能相互转化
D.在形变量相同时,劲度系数越大的弹簧,它的弹性势能越大
BCD
[针对训练3] (多选)有一劲度系数为k的弹簧,当弹簧从原长伸长Δl时弹力做功为W0.若规定弹簧处于原长时弹性势能为零,则下列叙述正确的是( )
A.使弹簧从原长伸长Δl时,弹力做正功W0,弹性势能Ep<0
B.使弹簧从原长压缩Δl时,弹力做负功W0,弹性势能Ep>0
C.使弹簧从伸长Δl变化到缩短Δl的过程中,弹力做2W0的正功
D.使弹簧从伸长Δl变化到缩短Δl的过程中,弹力做功为零
BD
[针对训练2] 弹簧原长l0=15 cm,受拉力作用后弹簧逐渐被拉长,当弹簧伸长到l1=20 cm时,作用在弹簧上的力为400 N,问:
(1)弹簧的劲度系数k为多少?
(2)在此过程中弹力做了多少功?
(3)弹簧的弹性势能变化了多少?
(1)8 000 N/m (2)-10 J (3)增大了10 J
课堂小结
2. 性质:
(1)相对性:
(2)系统性:
一、弹性势能
1. 定义:
3. 弹力做功与弹性势能变化的关系:
W弹 = - EP
弹力做功等于弹性势能变化量的相反数
4. 弹性势能表达式:
EP弹 = k x2
§8.22 弹性势能
第八章 机械能守恒定律
课前练.如图所示,有一连通器,左右两管的横截面积均为S,内盛密度为ρ的液体,开始时两管内的液面高度差为h。打开底部中央的阀门K,液体开始流动,最终两液面相平。在这一过程中,液体的重力加速度为g,液体的重力势能( )
A.减少 B.增加了
C.减少了 D.增加了
A
知识回顾
一、重力做的功
WG = mgh (h为高度差)
1. 表达式
2. 特点
物体运动时, 重力对它做的功只跟它的起点和终点的位置有关,而跟物体运动的路径无关 。
二、重力势能
EP = mgh (h为高度)
1. 表达式
2. 重力势能的系统性
3. 重力做功与重力势能变化的关系:
WG = EP1 - EP2
= - EP
4. 重力势能的相对性:
5. 绳子、链条类匀质物体重力势能的求法
一、弹性势能
1. 定义:发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫做弹性势能。
重力势能是由地球和
地面上物体的相对位置决定的
势能也叫位能
与相互作用的物体的相对位置有关。
弹性势能是由发生弹性形变的
物体各部分的相对位置决定的
2. 性质:
(1)相对性:弹簧处于原长时为零势能点。
(2)系统性:弹性势能是整个弹簧系统所具有的。
一、弹性势能
1. 定义:发生弹性形变的物体的各部分之间,由于有弹力的相互作用,
也具有势能,这种势能叫做弹性势能。
结合弹簧思考:弹性势能的大小可能与哪些因素有关?
课堂探究一:如图所示,滑块以初速度v冲向固定在竖直墙壁上的弹簧,
并将弹簧压缩.
(1)在弹簧压缩的过程中,分析弹簧弹力做功情况及弹性势能的变化;
(2)在弹簧恢复形变,从最大压缩量向原长恢复的过程中,
分析弹簧弹力做功情况及弹性势能的变化.
弹力做正功,弹性势能减小
弹力做负功,弹性势能增加
W弹 = - EP
2. 性质:
(1)相对性:弹簧处于原长时为零势能点。
(2)系统性:弹性势能是整个弹簧系统所具有的。
一、弹性势能
1. 定义:发生弹性形变的物体的各部分之间,由于有弹力的相互作用,
也具有势能,这种势能叫做弹性势能。
3. 弹力做功与弹性势能变化的关系:
W弹 = - EP
弹力做功等于弹性势能变化量的相反数
课堂探究一:如图所示,滑块以初速度v冲向固定在竖直墙壁上的弹簧,
并将弹簧压缩.
(1)在弹簧压缩的过程中,分析弹簧弹力做功情况及弹性势能的变化;
(2)在弹簧恢复形变,从最大压缩量向原长恢复的过程中,
分析弹簧弹力做功情况及弹性势能的变化.
(3)若弹簧劲度系数为k , 那么在弹簧压缩(或拉伸) x 的过程中,
求弹簧弹力做的功W弹 ?(用什么方法求?)
平均力法、图像法
2. 性质:
(1)相对性:弹簧处于原长时为零势能点。
(2)系统性:弹性势能是整个弹簧系统所具有的。
一、弹性势能
1. 定义:发生弹性形变的物体的各部分之间,由于有弹力的相互作用,
也具有势能,这种势能叫做弹性势能。
3. 弹力做功与弹性势能变化的关系:
W弹 = - EP
弹力做功等于弹性势能变化量的相反数
4. 弹性势能表达式:
EP弹 = k x2
弹簧的劲度系数
弹簧的形变量: 伸长量或压缩量
弹性势能的变化
弹力做功
重力做正功,重力势能减小
重力做负功,重力势能增加
弹力做正功,弹性势能减小
弹力做负功,弹性势能增加
W弹 = - EP
势能与力做功的关系
重力势能的变化
重力做功
WG = EP1 - EP2= - EP
[例3] (多选)关于弹性势能,下列说法正确的是( )
A.弹簧弹力做正功时,弹性势能增加
B.发生弹性形变的物体都具有弹性势能
C.弹性势能可以与其他形式的能相互转化
D.在形变量相同时,劲度系数越大的弹簧,它的弹性势能越大
BCD
[针对训练3] (多选)有一劲度系数为k的弹簧,当弹簧从原长伸长Δl时弹力做功为W0.若规定弹簧处于原长时弹性势能为零,则下列叙述正确的是( )
A.使弹簧从原长伸长Δl时,弹力做正功W0,弹性势能Ep<0
B.使弹簧从原长压缩Δl时,弹力做负功W0,弹性势能Ep>0
C.使弹簧从伸长Δl变化到缩短Δl的过程中,弹力做2W0的正功
D.使弹簧从伸长Δl变化到缩短Δl的过程中,弹力做功为零
BD
[针对训练2] 弹簧原长l0=15 cm,受拉力作用后弹簧逐渐被拉长,当弹簧伸长到l1=20 cm时,作用在弹簧上的力为400 N,问:
(1)弹簧的劲度系数k为多少?
(2)在此过程中弹力做了多少功?
(3)弹簧的弹性势能变化了多少?
(1)8 000 N/m (2)-10 J (3)增大了10 J
课堂小结
2. 性质:
(1)相对性:
(2)系统性:
一、弹性势能
1. 定义:
3. 弹力做功与弹性势能变化的关系:
W弹 = - EP
弹力做功等于弹性势能变化量的相反数
4. 弹性势能表达式:
EP弹 = k x2
