人教版八年级下册数学18.2.1矩形的性质课件(共19张PPT)
文档属性
| 名称 | 人教版八年级下册数学18.2.1矩形的性质课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 26.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 20:56:43 | ||
图片预览




文档简介
(共19张PPT)
18.2.1 矩形的性质(1)
第十八章 平行四边形
人教版 八年级数学 下册
边 角 对角线 对称性
平行四边形
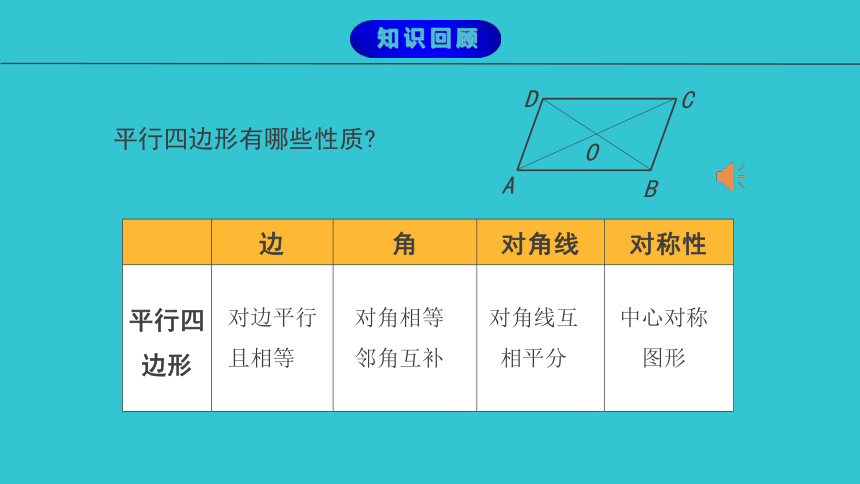
平行四边形有哪些性质
对边平行
且相等
对角相等
邻角互补
对角线互相平分
中心对称
图形
知识回顾
A
B
C
D
O
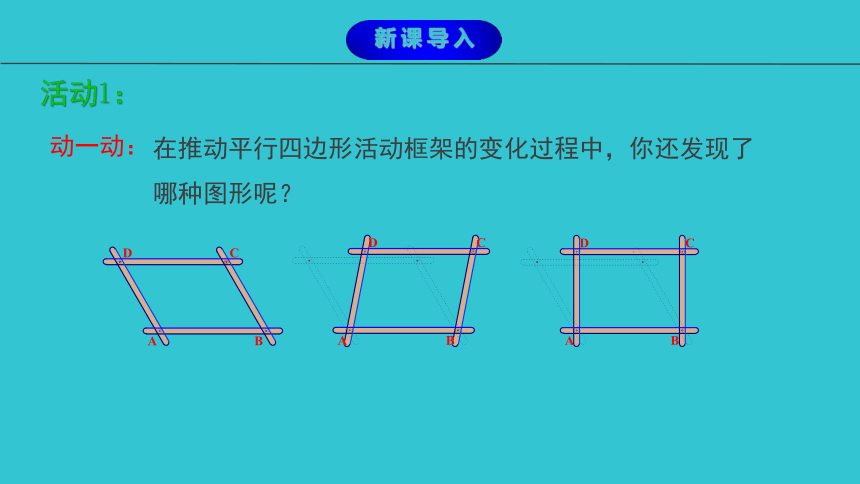
在推动平行四边形活动框架的变化过程中,你还发现了哪种图形呢?
动一动:
活动1:
新课导入
矩形在生活中无处不在.你还能举出身边矩形的例子吗?
新课导入
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形.
定义:有一个角是直角的平行四边形叫做矩形.
也叫做长方形.
概念归纳
一、矩形的定义
∠A ∠B ∠C ∠D AC BD
矩形1
矩形2
矩形3
小组
测量
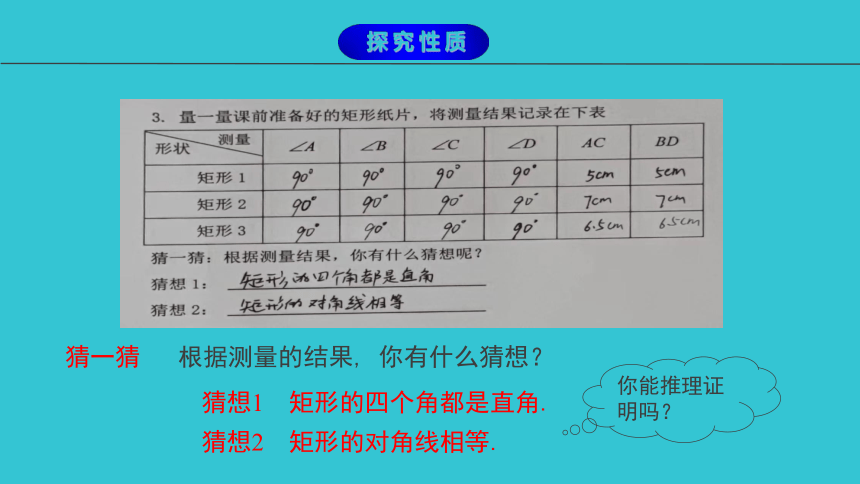
量一量 请同学们拿出课前准备好的大小不一的矩形纸片,测量矩形四个角的度数,对角线的长度,并记录测量结果.
探究性质
活动2:
猜想1 矩形的四个角都是直角.
猜想2 矩形的对角线相等.
你能推理证明吗?
猜一猜 根据测量的结果, 你有什么猜想?
探究性质
猜想1:矩形的四个角都是直角.
数学语言
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
性质1
已知:如图,四边形ABCD是矩形,∠A=90°
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
推理证明
性质归纳
证明:∵四边形ABCD是矩形,
∴∠C=∠A,∠B=∠D, AD∥BC.
∴∠A+∠B=180°.
又∵∠A = 90°,
∴∠B= 90°.
∴∠A=∠B=∠C=∠D =90
已知:如图,四边形ABCD是矩形
A
B
C
D
求证:AC=BD
猜想2:矩形的两条对角线相等.
数学语言
∵四边形ABCD是矩形
∴AC=BD
性质2
推理证明
性质归纳
思考 请同学们把矩形纸片,折一折,观察并思考.矩形是不是轴对称图形 如果是,那么对称轴有几条
矩形的性质:
对称性: .
对称轴: .
轴对称图形
2条
矩形 数学语言
边
角
对角线
对称性
对边平行且相等
四个角都是直角
相等且互相平分
中心对称图形
轴对称图形
A
B
C
D
性质归纳
二、矩形的性质
AB∥CD,AB=CD,AD∥BC,AD=BC
∠A=∠B=∠C=∠D=90°
AC=BD,AO=OB=OC=OD
例题 如图,在矩形ABCD中,两条对角线AC,BD相交于 点O,∠AOB=60°,AB=4 ,求矩形对角线的长.
解:∵四边形ABCD是矩形.
∴AC = BD,
OA= OC= AC,OB = OD = BD ,
∴OA = OB.
又∵∠AOB=60°,
∴△OAB是等边三角形,
∴OA=AB=4,
∴AC=BD=2OA=8.
A
B
C
D
O
矩形的对角线相等且互相平分
性质运用
如图,在矩形ABCD中,对角线AC,BD相交于点O.
D
C
B
A
O
(1)若∠BAC=60°,则∠BCA=____;
(2)若AC=8㎝,则BD=_____㎝;
(3)图中共有_____个等腰三角形;
30°
8
4
小试牛刀
A
B
C
D
O
活动3 如图,一张矩形纸片,画出两条对角线,沿着对角线AC剪去一半.
B
C
O
A
问题 Rt△ABC中,BO是一条怎样的线段?
它的长度与斜边AC有什么关系?
直角三角中线性质
数学语言:
中,为斜边中点,
归纳总结
A
B
C
O
三、直角三角形的斜边中线定理
性质:直角三角形斜边上的中线等于斜边的一半.
思考 有三位学生正在做投圈游戏,他们分别站在一个直角三角形的三个顶点处,目标物放在斜边的中点处. 三个人的位置对每个人公平吗?请说明理由.
性质运用
矩形的相关概念及性质
具有平行四边形的一切性质
四个内角都是直角,
两条对角线互相平分且相等
轴对称图形
有两条对称轴
直角三角形斜边上的中线等于斜边的一半
有一个角是直角的平行四边形叫做矩形
通过本节课的学习,你有哪些收获?
课堂小结
2.如图,在矩形ABCD中,点E是BC上一点,
AE=AD,DF⊥AE,垂足为F.求证:DF=DC.
A
F
B
C
D
o
必做题
选做题
A
B
C
E
D
F
布置作业
如图,在矩形ABCD中,对角线AC,BD相交于点O,且∠CDF=∠BDC,∠DCF=∠ACD.求证:DF=CF.
1.矩形具有一般平行四边形而不具有的性质是 ( )
B.对边相等
A.对角相等
C.对角线相等
D.对角线互相平分
谢 谢 聆 听 !
18.2.1 矩形的性质(1)
第十八章 平行四边形
人教版 八年级数学 下册
边 角 对角线 对称性
平行四边形
平行四边形有哪些性质
对边平行
且相等
对角相等
邻角互补
对角线互相平分
中心对称
图形
知识回顾
A
B
C
D
O
在推动平行四边形活动框架的变化过程中,你还发现了哪种图形呢?
动一动:
活动1:
新课导入
矩形在生活中无处不在.你还能举出身边矩形的例子吗?
新课导入
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形.
定义:有一个角是直角的平行四边形叫做矩形.
也叫做长方形.
概念归纳
一、矩形的定义
∠A ∠B ∠C ∠D AC BD
矩形1
矩形2
矩形3
小组
测量
量一量 请同学们拿出课前准备好的大小不一的矩形纸片,测量矩形四个角的度数,对角线的长度,并记录测量结果.
探究性质
活动2:
猜想1 矩形的四个角都是直角.
猜想2 矩形的对角线相等.
你能推理证明吗?
猜一猜 根据测量的结果, 你有什么猜想?
探究性质
猜想1:矩形的四个角都是直角.
数学语言
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
性质1
已知:如图,四边形ABCD是矩形,∠A=90°
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
推理证明
性质归纳
证明:∵四边形ABCD是矩形,
∴∠C=∠A,∠B=∠D, AD∥BC.
∴∠A+∠B=180°.
又∵∠A = 90°,
∴∠B= 90°.
∴∠A=∠B=∠C=∠D =90
已知:如图,四边形ABCD是矩形
A
B
C
D
求证:AC=BD
猜想2:矩形的两条对角线相等.
数学语言
∵四边形ABCD是矩形
∴AC=BD
性质2
推理证明
性质归纳
思考 请同学们把矩形纸片,折一折,观察并思考.矩形是不是轴对称图形 如果是,那么对称轴有几条
矩形的性质:
对称性: .
对称轴: .
轴对称图形
2条
矩形 数学语言
边
角
对角线
对称性
对边平行且相等
四个角都是直角
相等且互相平分
中心对称图形
轴对称图形
A
B
C
D
性质归纳
二、矩形的性质
AB∥CD,AB=CD,AD∥BC,AD=BC
∠A=∠B=∠C=∠D=90°
AC=BD,AO=OB=OC=OD
例题 如图,在矩形ABCD中,两条对角线AC,BD相交于 点O,∠AOB=60°,AB=4 ,求矩形对角线的长.
解:∵四边形ABCD是矩形.
∴AC = BD,
OA= OC= AC,OB = OD = BD ,
∴OA = OB.
又∵∠AOB=60°,
∴△OAB是等边三角形,
∴OA=AB=4,
∴AC=BD=2OA=8.
A
B
C
D
O
矩形的对角线相等且互相平分
性质运用
如图,在矩形ABCD中,对角线AC,BD相交于点O.
D
C
B
A
O
(1)若∠BAC=60°,则∠BCA=____;
(2)若AC=8㎝,则BD=_____㎝;
(3)图中共有_____个等腰三角形;
30°
8
4
小试牛刀
A
B
C
D
O
活动3 如图,一张矩形纸片,画出两条对角线,沿着对角线AC剪去一半.
B
C
O
A
问题 Rt△ABC中,BO是一条怎样的线段?
它的长度与斜边AC有什么关系?
直角三角中线性质
数学语言:
中,为斜边中点,
归纳总结
A
B
C
O
三、直角三角形的斜边中线定理
性质:直角三角形斜边上的中线等于斜边的一半.
思考 有三位学生正在做投圈游戏,他们分别站在一个直角三角形的三个顶点处,目标物放在斜边的中点处. 三个人的位置对每个人公平吗?请说明理由.
性质运用
矩形的相关概念及性质
具有平行四边形的一切性质
四个内角都是直角,
两条对角线互相平分且相等
轴对称图形
有两条对称轴
直角三角形斜边上的中线等于斜边的一半
有一个角是直角的平行四边形叫做矩形
通过本节课的学习,你有哪些收获?
课堂小结
2.如图,在矩形ABCD中,点E是BC上一点,
AE=AD,DF⊥AE,垂足为F.求证:DF=DC.
A
F
B
C
D
o
必做题
选做题
A
B
C
E
D
F
布置作业
如图,在矩形ABCD中,对角线AC,BD相交于点O,且∠CDF=∠BDC,∠DCF=∠ACD.求证:DF=CF.
1.矩形具有一般平行四边形而不具有的性质是 ( )
B.对边相等
A.对角相等
C.对角线相等
D.对角线互相平分
谢 谢 聆 听 !
