【备考2023】浙教版科学中考第三轮冲刺讲义(三十 ):推导证明专题【word,含答案】
文档属性
| 名称 | 【备考2023】浙教版科学中考第三轮冲刺讲义(三十 ):推导证明专题【word,含答案】 |

|
|
| 格式 | doc | ||
| 文件大小 | 734.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2023-03-22 00:00:00 | ||
图片预览




文档简介
(1)把握问题重点。
(2)根据审题的几个方面确定答案要点,根据理顺的思路针对题目进行回答。
(3)①明确科学本质,确定知识点,确定基本公式,并按照公式逐步推导,演化,替代;
②将科学结论转化为用科学公式表达,需要学生运用较多科学语言(文字或科学公式等),并运用因果关系,体现一定逻辑顺序。
例1、如图所示,一根质量分布均匀的木棒,质量为m,长度为L,竖直悬挂在转轴O处。在木棒最下端用一方向始终水平向右的拉力F缓慢将木棒拉动到竖直方向夹角为θ的位置(转轴处摩擦不计)。问:
(1)在答题纸上画出θ=60°时拉力F的力臂l,并计算力臂的大小。
(2)木棒的重力作用点在其长度二分之一处,随拉开角度θ的增加,拉力F将如何变化?并推导拉力F与角度θ的关系式。
例2、小金用如图所示的实验装置测量杠杆的机械效率。实验时竖直向上拉动杠杆,使挂在杠杆下面的钩码缓缓上升。(支点和杠杆的摩擦不计)问:
(1)重为5N的钩码挂在A点时,人的拉力F为4N。钩码上升0.3m时,动力作用点C上升0.5m,此时机械效率 η1为多大?
(2)小金为了进一步研究杠杆的机械效率与哪些因素有关,仍用该实验装置,将钩码移到 B点,再次缓慢提升杠杆使动力作用点C仍然上升0.5m。问:与第一次相比,人的拉力 F将 (选填“变大”“变小”或“不变”)。比较此时的机械效率η2与η1的大小,并用学过的知识给以推导。
例3、如图是小金研究电动机 ( http: / / www.21cnjy.com )转动是否对小灯泡的亮度有影响的电路图。开始小金先抓住转轴合上开关,观察小灯泡的亮度;接着放开转轴让电动机转动,继续观察小灯泡亮度的变化(已知:小灯泡的电阻为R,电动机线圈电阻为r,电源电压为U)。由此请你回答:
(1)在电动机未转动时,t时间内电流在电路中产生的热量为 ______(填写表达式)。
(2)在电动机转动时,电流所做的功________电流在电路中产生的热量(选填“大于”、“等于”或“小于”)。
(3)小金判断电动机转动后小灯泡会更亮,你认为小金的判断正确吗?并根据学过后知识给以解释。
例4、甲、乙两位同学对“雨滴的下落速度是否跟雨滴的大小有关”持有不同的意见,于是他们对此展开研究。他们从网上查到,雨滴在下落过程中接近地面时受到的空气阻力与雨滴的横截面积S成正比,与雨滴下落速度v的平方成正比,即f=kSv2(其中k为比例系数,是个定值),雨滴接近地面时可看做匀速直线运动。把雨滴看做球形,其半径为r,密度为ρ,比热为c,球的体积为Vπr3.(注:所有结果均用字母表示)
(1)半径为r的雨滴重力为 。
(2)在接近地面时,大雨滴的下落速度 小雨滴的下落速度(选填“大于”“等于”“小于”),写出推理过程。
(3)假设半径为r的雨滴在近地面下落h高度的过程中,重力对它所做的功全部转化为雨滴的内能,则雨滴的温度升高了多少?
1.凸透镜成像时,物距u,像距ν和焦距f之间的关系可以用公式表示。如图所示,物体AB垂直于主光轴放在凸透镜(图中L表示凸透镜)前,O点为光心,F为焦点,P为2倍焦距处。
(1)请在图中作出物体AB所成的像A'B'。
(2)已知凸透镜成等大的像时v=u,证明当凸透镜成等大的实像时u=2f。
(3)物理学中用像距和物距的比值来表示凸透镜的放大率,即m。请你结合公式和投影仪成像时u和v的大小关系,说明投影仪成像时放大率m是大于1还是小于1。
2.做功的实质是将一种形式的能量转化为另一种形式的能量。运动的物体克服摩擦做功的实质是将机械能转化为内能,若一个质量为m,初始速度为v的物块在水平面上沿直线滑行时,受到的摩擦力使物块最终停下,测量出物块滑行的距离为s(动能的表达式为Emv2)。
(1)试推导物块的初始速度v。
(2)若一辆时速为20m/s,质量为1.8×103kg的小汽车紧急刹车距离为36m,求汽车在刹车过程中受到的摩擦力大小。
3.某电热杯中有甲、乙两根电热丝,只将甲电热丝接到电源上时,烧开一杯水需要的时间为t1;只将乙电热丝接到电源上时,烧开同样的一杯水需需要的时间为t2.若R甲>R乙,则 t1 t2则(填“>”、“<”或“=”).证明若将甲、乙并联起来接到电源上时,烧开同样的一杯水需要的时间为(设电源电压不变,不计热量损失)。
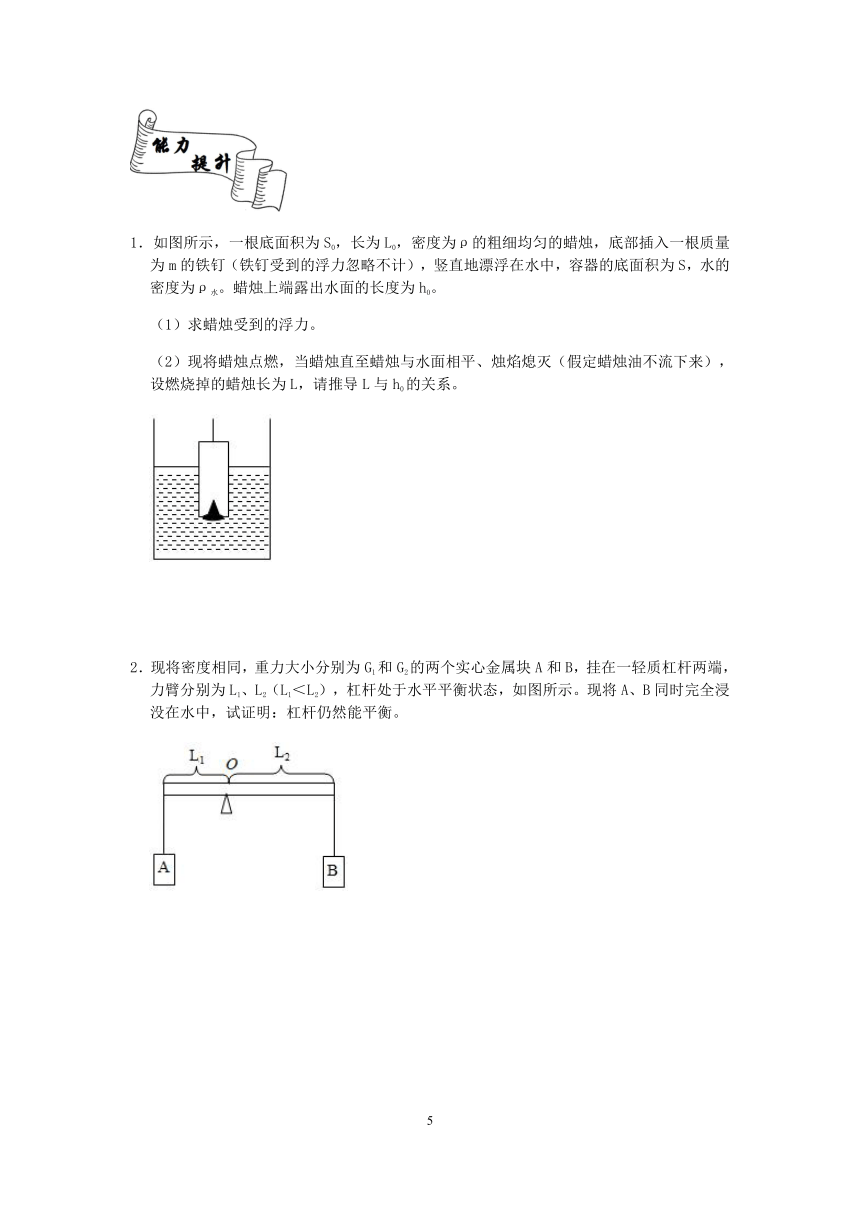
1.如图所示,一根底面积为S0,长为L0,密度为ρ的粗细均匀的蜡烛,底部插入一根质量为m的铁钉(铁钉受到的浮力忽略不计),竖直地漂浮在水中,容器的底面积为S,水的密度为ρ水。蜡烛上端露出水面的长度为h0。
(1)求蜡烛受到的浮力。
(2)现将蜡烛点燃,当蜡烛直至蜡烛与水面相平、烛焰熄灭(假定蜡烛油不流下来),设燃烧掉的蜡烛长为L,请推导L与h0的关系。
2.现将密度相同,重力大小分别为G1和G2的两个实心金属块A和B,挂在一轻质杠杆两端,力臂分别为L1、L2(L1<L2),杠杆处于水平平衡状态,如图所示。现将A、B同时完全浸没在水中,试证明:杠杆仍然能平衡。
3.如图所示为一块方形玻璃砖,光线AB从空气斜射进来。BC是光线AB的折射光线,其中MN和PQ是法线并且互相平行。
(1)作出BC光线从玻璃出来后的光线CD;
(2)请利用几何知识和光学知识,求证:AB//CD。
4.如图甲为一个底面积为S0的圆柱形容器,内部装有深度为h1密度为ρ的水,图乙为一边长为a的正方体木块,图丙为一质量为m的正方体冰块。请用题中物理量符号推导:
(1)将木块放入容器内的水中,木块漂浮,木块上表面到水面距离为h2,则木块密度为 ;
(2)将冰块放到(1)中漂浮的木块上,此时容器中水面又将升高的高度Δh= ;(水不溢出,块仍然漂浮)
(3)请推导说明(2)中冰块熔化后,圆柱形容器中液面升降情况。
参考答案
例1、
(1)如右图所示,l= L×cos60°=0.5L
(2)F随拉开的角度θ的增加将变大
根据杠杆平衡条件可得
mg×0.5 ×L×sinθ=F ×L×cosθ
F=0.5mgtanθ
例2、(1)75% (2)变小 η2<η1
(1)
(2)将钩码移到 B点时,重物G的阻力臂LG减小,而G、杆的自重G0及其力臂LG0、动力臂LF均不变,由杠杆平衡条件GLG+G0LG0=FLF,可知拉力F将变小。
第二次提升时,杠杆升高的高度不变,因此克服杠杆自重所做的额外功不变。而被提升的砝码由于靠近支点,因此砝码升高的高度减小,有用功减小。由
而W有2< W有1,W额外不变,则可退知η2<η1
例3、(1)t(2)大于
(3)不正确,不转时W总功=Q电路 UI1t=I12(R+r)t I1=;
转动时W’总功>Q’电路 UI2t>I22(R+r)t I2<,故I2< I1,灯泡变暗
例4、解:
(1)雨滴的体积:Vπr3,
则根据ρ得,其质量m=ρVπr3ρ,
故重力G=mgπr3ρg;
(2)雨滴接近地面时可看做匀速直线运动,故f=G,
因为f=kSv2=kπr2v2,Gπr3ρg,
所以,kπr2v2πr3ρg,
化简得,v,
又因为k、ρ、g均为定值,
所以,r越大,速度越大,
即在接近地面时,大雨滴的下落速度大于小雨滴的下落速度。
(3)设雨滴的质量为m,
因为重力对它所做的功全部转化为雨滴的内能,即W=Q,
又因为W=Gh=mgh,Q=cm△t,
所以,mgh=cm△t,
则△t。
答:(1)πr3ρg;(2)大于;推理过程详见解答;(3)雨滴的温度升高了。
1.解:(1)经过光心光线不改变方向;平行于主光轴光线折射经过右焦点。两条光线交点就是成像点,光路图如图所示:
(2)由题意,凸透镜成等大的像时v=u,
将v=u,带入公式可得,
,
化简可得u=2f;
(3)投影仪能成放大的实像,v>u,1,可得m>1,即投影仪成像时放大率m是大于1。
故答案为:(1)见上图;(2)见解答部分;(3)投影仪成像时放大率m是大于1。
2.解:
(1)运动的物体克服摩擦做功的实质是将机械能转化为内能,且物体的初始速度为v,末速度为0,
所以W=Ek﹣0,即fsmv2﹣0,
物块的初始速度v;
(2)运动的物体克服摩擦做功的实质是将机械能转化为内能,
即fsmv2,
代入数据,
汽车在刹车过程中受到的摩擦力:
f10000N。
答:(1)见解答;(2)汽车在刹车过程中受到的摩擦力为10000N。
3.解:(1)烧开同样的一杯水消耗的电能相等,
因R甲>R乙,
所以,由Wt的变形式t可知,t1>t2;
(2)由Wt可得,甲、乙两根电热丝的电阻分别为:
R甲,R乙,
将甲、乙并联起来接到电源上时,
因并联电路中总电阻的倒数等于各分电阻倒数之和,
所以,电路中的总电阻:
R,
则需要的加热时间:
tR。
答:>;证明过程如上所示。
1.解:
(1)图中蜡烛浸入水中的深度h浸=L0﹣h0,
则蜡烛受到的浮力:F浮=ρ水gS0(L0﹣h0);
(2)图中蜡烛处于漂浮状态,则由F浮=G蜡+G铁可得:ρ水gS0(L0﹣h0)=ρgS0L0+mg﹣﹣﹣﹣﹣①
点燃蜡烛,直至蜡烛与水面相平、烛焰熄灭,且燃烧掉的蜡烛长为L,
此时蜡烛和铁钉悬浮,则:F浮′=G蜡′+G铁,
即:ρ水gS0(L0﹣L)=ρgS0(L0﹣L)+mg﹣﹣﹣﹣﹣﹣②
①﹣②得:
ρ水g(L﹣h0)=ρgL,
解得:L。
答:(1)蜡烛受到的浮力为ρ水gS0(L0﹣h0);
(2)L与h0的关系:L。
2.证明:杠杆两端分别挂上同种材料大小不同的实心金属块时,杠杆在水平位置平衡,
根据重力公式和杠杆的平衡条件可得:ρVAg×L1=ρVBg×L2,
所以:VA×L1=VB×L2,
若将两金属块同时浸没在水中,则:
左端力和力臂的乘积=(GA﹣F浮A)L1=(ρVAg﹣ρ水VAg)×L1=(ρ﹣ρ水)×VAg×L1,
右端力和力臂的乘积=(GB﹣F浮B)L2=(ρVBg﹣ρ水VBg)×L2=(ρ﹣ρ水)×VBg×L2,
因为VA×L1=VB×L2,
所以(ρ﹣ρ水)×VAg×L1=(ρ﹣ρ水)×VBg×L2,
因此A、B同时浸没在水中时,杠杆仍然能平衡。
3.解:(1)光线BC从玻璃砖斜射进入空气,折射光线CD远离法线偏折,折射角大于入射角,如图所示:
;
(2)如下图所示,延长AB,反向延长最后的折射光线CD:
;
图中∠1为入射角,∠2为折射角;MN和PQ是法线并且互相平行,所以∠2=∠3;在光的折射中,光路是可逆的,所以∠4=∠1;∠4和∠5互为余角,∠θ与∠1互为余角,则∠5=∠θ;对顶角相等,即∠5=∠6,所以∠6=∠θ,玻璃砖的上下两个面是平行的,所以AB平行于CD。
4.解:(1)木块漂浮,所以F浮=G木,即ρgV排=ρ木gV木,
所以ρga2(a﹣h2)=ρ木ga3,
则木块密度为:
ρ木;
(2)将冰块放到(1)中漂浮的木块上,此时木块和冰块仍漂浮,浮力等于木块和冰块的总重力,
增加的浮力等于冰块的重力,ΔF浮=ρgΔV排=G冰=mg,
增加的排开水的体积为:
ΔV排,
此时容器中水面又将升高的高度为:
Δh;
(3)冰块漂浮,则F浮′=G冰,
ρV排g=G冰=mg
可得V排;
冰熔化前后质量不变,G冰=G冰化水=ρV冰化水g=mg
V排和V冰化水相等,
所以冰熔化前后水面不升也不降。
答:(1);(2);(3)冰熔化前后水面不升也不降。
【备考2023】浙教版科学中考第三轮冲刺讲义(三十)
推导证明专题
(2)根据审题的几个方面确定答案要点,根据理顺的思路针对题目进行回答。
(3)①明确科学本质,确定知识点,确定基本公式,并按照公式逐步推导,演化,替代;
②将科学结论转化为用科学公式表达,需要学生运用较多科学语言(文字或科学公式等),并运用因果关系,体现一定逻辑顺序。
例1、如图所示,一根质量分布均匀的木棒,质量为m,长度为L,竖直悬挂在转轴O处。在木棒最下端用一方向始终水平向右的拉力F缓慢将木棒拉动到竖直方向夹角为θ的位置(转轴处摩擦不计)。问:
(1)在答题纸上画出θ=60°时拉力F的力臂l,并计算力臂的大小。
(2)木棒的重力作用点在其长度二分之一处,随拉开角度θ的增加,拉力F将如何变化?并推导拉力F与角度θ的关系式。
例2、小金用如图所示的实验装置测量杠杆的机械效率。实验时竖直向上拉动杠杆,使挂在杠杆下面的钩码缓缓上升。(支点和杠杆的摩擦不计)问:
(1)重为5N的钩码挂在A点时,人的拉力F为4N。钩码上升0.3m时,动力作用点C上升0.5m,此时机械效率 η1为多大?
(2)小金为了进一步研究杠杆的机械效率与哪些因素有关,仍用该实验装置,将钩码移到 B点,再次缓慢提升杠杆使动力作用点C仍然上升0.5m。问:与第一次相比,人的拉力 F将 (选填“变大”“变小”或“不变”)。比较此时的机械效率η2与η1的大小,并用学过的知识给以推导。
例3、如图是小金研究电动机 ( http: / / www.21cnjy.com )转动是否对小灯泡的亮度有影响的电路图。开始小金先抓住转轴合上开关,观察小灯泡的亮度;接着放开转轴让电动机转动,继续观察小灯泡亮度的变化(已知:小灯泡的电阻为R,电动机线圈电阻为r,电源电压为U)。由此请你回答:
(1)在电动机未转动时,t时间内电流在电路中产生的热量为 ______(填写表达式)。
(2)在电动机转动时,电流所做的功________电流在电路中产生的热量(选填“大于”、“等于”或“小于”)。
(3)小金判断电动机转动后小灯泡会更亮,你认为小金的判断正确吗?并根据学过后知识给以解释。
例4、甲、乙两位同学对“雨滴的下落速度是否跟雨滴的大小有关”持有不同的意见,于是他们对此展开研究。他们从网上查到,雨滴在下落过程中接近地面时受到的空气阻力与雨滴的横截面积S成正比,与雨滴下落速度v的平方成正比,即f=kSv2(其中k为比例系数,是个定值),雨滴接近地面时可看做匀速直线运动。把雨滴看做球形,其半径为r,密度为ρ,比热为c,球的体积为Vπr3.(注:所有结果均用字母表示)
(1)半径为r的雨滴重力为 。
(2)在接近地面时,大雨滴的下落速度 小雨滴的下落速度(选填“大于”“等于”“小于”),写出推理过程。
(3)假设半径为r的雨滴在近地面下落h高度的过程中,重力对它所做的功全部转化为雨滴的内能,则雨滴的温度升高了多少?
1.凸透镜成像时,物距u,像距ν和焦距f之间的关系可以用公式表示。如图所示,物体AB垂直于主光轴放在凸透镜(图中L表示凸透镜)前,O点为光心,F为焦点,P为2倍焦距处。
(1)请在图中作出物体AB所成的像A'B'。
(2)已知凸透镜成等大的像时v=u,证明当凸透镜成等大的实像时u=2f。
(3)物理学中用像距和物距的比值来表示凸透镜的放大率,即m。请你结合公式和投影仪成像时u和v的大小关系,说明投影仪成像时放大率m是大于1还是小于1。
2.做功的实质是将一种形式的能量转化为另一种形式的能量。运动的物体克服摩擦做功的实质是将机械能转化为内能,若一个质量为m,初始速度为v的物块在水平面上沿直线滑行时,受到的摩擦力使物块最终停下,测量出物块滑行的距离为s(动能的表达式为Emv2)。
(1)试推导物块的初始速度v。
(2)若一辆时速为20m/s,质量为1.8×103kg的小汽车紧急刹车距离为36m,求汽车在刹车过程中受到的摩擦力大小。
3.某电热杯中有甲、乙两根电热丝,只将甲电热丝接到电源上时,烧开一杯水需要的时间为t1;只将乙电热丝接到电源上时,烧开同样的一杯水需需要的时间为t2.若R甲>R乙,则 t1 t2则(填“>”、“<”或“=”).证明若将甲、乙并联起来接到电源上时,烧开同样的一杯水需要的时间为(设电源电压不变,不计热量损失)。
1.如图所示,一根底面积为S0,长为L0,密度为ρ的粗细均匀的蜡烛,底部插入一根质量为m的铁钉(铁钉受到的浮力忽略不计),竖直地漂浮在水中,容器的底面积为S,水的密度为ρ水。蜡烛上端露出水面的长度为h0。
(1)求蜡烛受到的浮力。
(2)现将蜡烛点燃,当蜡烛直至蜡烛与水面相平、烛焰熄灭(假定蜡烛油不流下来),设燃烧掉的蜡烛长为L,请推导L与h0的关系。
2.现将密度相同,重力大小分别为G1和G2的两个实心金属块A和B,挂在一轻质杠杆两端,力臂分别为L1、L2(L1<L2),杠杆处于水平平衡状态,如图所示。现将A、B同时完全浸没在水中,试证明:杠杆仍然能平衡。
3.如图所示为一块方形玻璃砖,光线AB从空气斜射进来。BC是光线AB的折射光线,其中MN和PQ是法线并且互相平行。
(1)作出BC光线从玻璃出来后的光线CD;
(2)请利用几何知识和光学知识,求证:AB//CD。
4.如图甲为一个底面积为S0的圆柱形容器,内部装有深度为h1密度为ρ的水,图乙为一边长为a的正方体木块,图丙为一质量为m的正方体冰块。请用题中物理量符号推导:
(1)将木块放入容器内的水中,木块漂浮,木块上表面到水面距离为h2,则木块密度为 ;
(2)将冰块放到(1)中漂浮的木块上,此时容器中水面又将升高的高度Δh= ;(水不溢出,块仍然漂浮)
(3)请推导说明(2)中冰块熔化后,圆柱形容器中液面升降情况。
参考答案
例1、
(1)如右图所示,l= L×cos60°=0.5L
(2)F随拉开的角度θ的增加将变大
根据杠杆平衡条件可得
mg×0.5 ×L×sinθ=F ×L×cosθ
F=0.5mgtanθ
例2、(1)75% (2)变小 η2<η1
(1)
(2)将钩码移到 B点时,重物G的阻力臂LG减小,而G、杆的自重G0及其力臂LG0、动力臂LF均不变,由杠杆平衡条件GLG+G0LG0=FLF,可知拉力F将变小。
第二次提升时,杠杆升高的高度不变,因此克服杠杆自重所做的额外功不变。而被提升的砝码由于靠近支点,因此砝码升高的高度减小,有用功减小。由
而W有2< W有1,W额外不变,则可退知η2<η1
例3、(1)t(2)大于
(3)不正确,不转时W总功=Q电路 UI1t=I12(R+r)t I1=;
转动时W’总功>Q’电路 UI2t>I22(R+r)t I2<,故I2< I1,灯泡变暗
例4、解:
(1)雨滴的体积:Vπr3,
则根据ρ得,其质量m=ρVπr3ρ,
故重力G=mgπr3ρg;
(2)雨滴接近地面时可看做匀速直线运动,故f=G,
因为f=kSv2=kπr2v2,Gπr3ρg,
所以,kπr2v2πr3ρg,
化简得,v,
又因为k、ρ、g均为定值,
所以,r越大,速度越大,
即在接近地面时,大雨滴的下落速度大于小雨滴的下落速度。
(3)设雨滴的质量为m,
因为重力对它所做的功全部转化为雨滴的内能,即W=Q,
又因为W=Gh=mgh,Q=cm△t,
所以,mgh=cm△t,
则△t。
答:(1)πr3ρg;(2)大于;推理过程详见解答;(3)雨滴的温度升高了。
1.解:(1)经过光心光线不改变方向;平行于主光轴光线折射经过右焦点。两条光线交点就是成像点,光路图如图所示:
(2)由题意,凸透镜成等大的像时v=u,
将v=u,带入公式可得,
,
化简可得u=2f;
(3)投影仪能成放大的实像,v>u,1,可得m>1,即投影仪成像时放大率m是大于1。
故答案为:(1)见上图;(2)见解答部分;(3)投影仪成像时放大率m是大于1。
2.解:
(1)运动的物体克服摩擦做功的实质是将机械能转化为内能,且物体的初始速度为v,末速度为0,
所以W=Ek﹣0,即fsmv2﹣0,
物块的初始速度v;
(2)运动的物体克服摩擦做功的实质是将机械能转化为内能,
即fsmv2,
代入数据,
汽车在刹车过程中受到的摩擦力:
f10000N。
答:(1)见解答;(2)汽车在刹车过程中受到的摩擦力为10000N。
3.解:(1)烧开同样的一杯水消耗的电能相等,
因R甲>R乙,
所以,由Wt的变形式t可知,t1>t2;
(2)由Wt可得,甲、乙两根电热丝的电阻分别为:
R甲,R乙,
将甲、乙并联起来接到电源上时,
因并联电路中总电阻的倒数等于各分电阻倒数之和,
所以,电路中的总电阻:
R,
则需要的加热时间:
tR。
答:>;证明过程如上所示。
1.解:
(1)图中蜡烛浸入水中的深度h浸=L0﹣h0,
则蜡烛受到的浮力:F浮=ρ水gS0(L0﹣h0);
(2)图中蜡烛处于漂浮状态,则由F浮=G蜡+G铁可得:ρ水gS0(L0﹣h0)=ρgS0L0+mg﹣﹣﹣﹣﹣①
点燃蜡烛,直至蜡烛与水面相平、烛焰熄灭,且燃烧掉的蜡烛长为L,
此时蜡烛和铁钉悬浮,则:F浮′=G蜡′+G铁,
即:ρ水gS0(L0﹣L)=ρgS0(L0﹣L)+mg﹣﹣﹣﹣﹣﹣②
①﹣②得:
ρ水g(L﹣h0)=ρgL,
解得:L。
答:(1)蜡烛受到的浮力为ρ水gS0(L0﹣h0);
(2)L与h0的关系:L。
2.证明:杠杆两端分别挂上同种材料大小不同的实心金属块时,杠杆在水平位置平衡,
根据重力公式和杠杆的平衡条件可得:ρVAg×L1=ρVBg×L2,
所以:VA×L1=VB×L2,
若将两金属块同时浸没在水中,则:
左端力和力臂的乘积=(GA﹣F浮A)L1=(ρVAg﹣ρ水VAg)×L1=(ρ﹣ρ水)×VAg×L1,
右端力和力臂的乘积=(GB﹣F浮B)L2=(ρVBg﹣ρ水VBg)×L2=(ρ﹣ρ水)×VBg×L2,
因为VA×L1=VB×L2,
所以(ρ﹣ρ水)×VAg×L1=(ρ﹣ρ水)×VBg×L2,
因此A、B同时浸没在水中时,杠杆仍然能平衡。
3.解:(1)光线BC从玻璃砖斜射进入空气,折射光线CD远离法线偏折,折射角大于入射角,如图所示:
;
(2)如下图所示,延长AB,反向延长最后的折射光线CD:
;
图中∠1为入射角,∠2为折射角;MN和PQ是法线并且互相平行,所以∠2=∠3;在光的折射中,光路是可逆的,所以∠4=∠1;∠4和∠5互为余角,∠θ与∠1互为余角,则∠5=∠θ;对顶角相等,即∠5=∠6,所以∠6=∠θ,玻璃砖的上下两个面是平行的,所以AB平行于CD。
4.解:(1)木块漂浮,所以F浮=G木,即ρgV排=ρ木gV木,
所以ρga2(a﹣h2)=ρ木ga3,
则木块密度为:
ρ木;
(2)将冰块放到(1)中漂浮的木块上,此时木块和冰块仍漂浮,浮力等于木块和冰块的总重力,
增加的浮力等于冰块的重力,ΔF浮=ρgΔV排=G冰=mg,
增加的排开水的体积为:
ΔV排,
此时容器中水面又将升高的高度为:
Δh;
(3)冰块漂浮,则F浮′=G冰,
ρV排g=G冰=mg
可得V排;
冰熔化前后质量不变,G冰=G冰化水=ρV冰化水g=mg
V排和V冰化水相等,
所以冰熔化前后水面不升也不降。
答:(1);(2);(3)冰熔化前后水面不升也不降。
【备考2023】浙教版科学中考第三轮冲刺讲义(三十)
推导证明专题
同课章节目录
