2022-2023学年人教版数学七年级下册 5.1 相交线(课时1)同步练习(含答案)
文档属性
| 名称 | 2022-2023学年人教版数学七年级下册 5.1 相交线(课时1)同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 184.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-24 08:39:21 | ||
图片预览

文档简介
《5.1 相交线》同步练习
(课时1 相交线)
一、基础巩固
知识点1 邻补角的定义与性质
1. [2022重庆荣昌区期末]下列各图中,∠1与∠2是邻补角的是 ( )
2. 如图,直线AB,CD相交所成的四个角中,∠1的邻补角为 ,若∠1∶∠2=1∶3,则∠1的度数为 .
知识点2 对顶角的定义与性质
3. [2022秦皇岛期中]下列各图中,∠1与∠2是对顶角的是 ( )
4. [2022北京中考]如图,利用工具测量角,则∠1的大小为 ( )
A.30° B.60° C.120° D.150°
5. 如图,直线AB与CD相交于点O,若∠AOC=75°,∠1=25°,则∠2的度数是 ( )
A.25° B.30° C.40° D.50°
知识点3 邻补角与对顶角的综合应用
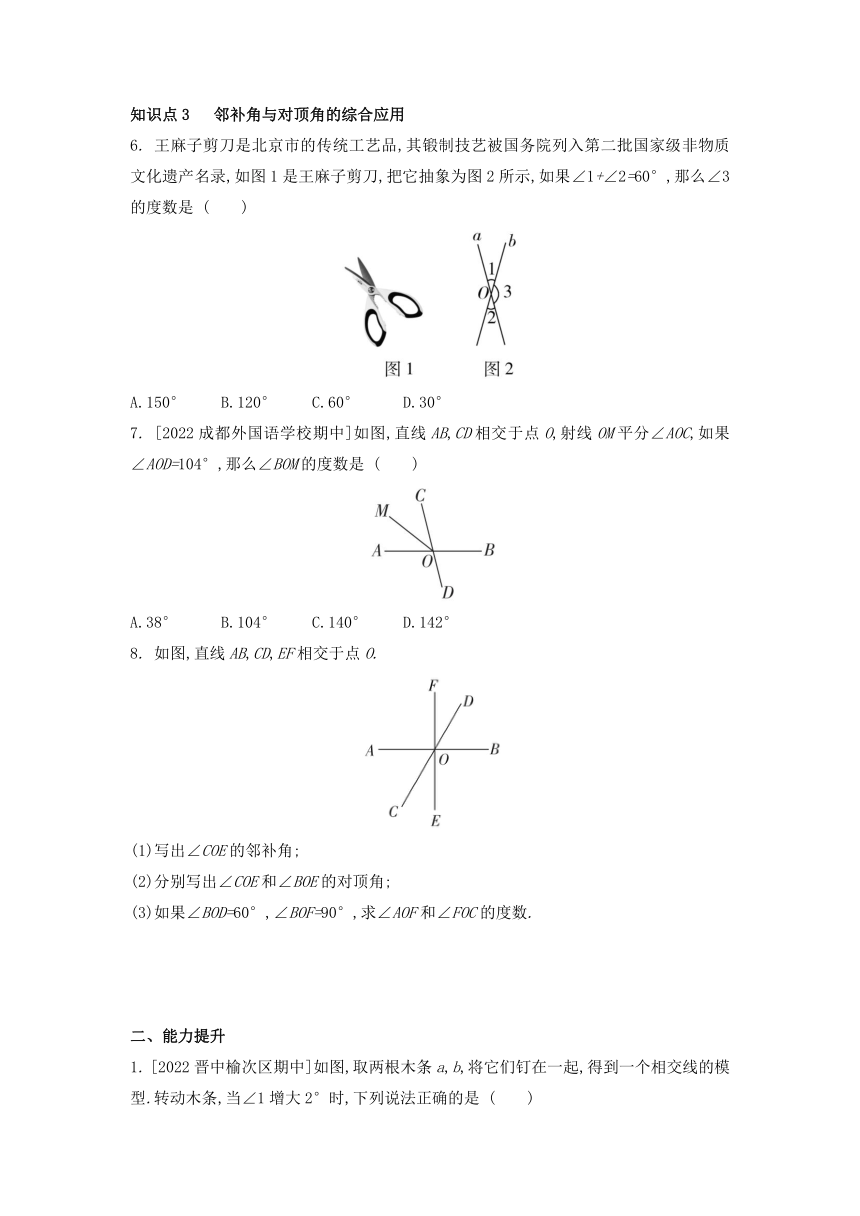
6. 王麻子剪刀是北京市的传统工艺品,其锻制技艺被国务院列入第二批国家级非物质文化遗产名录,如图1是王麻子剪刀,把它抽象为图2所示,如果∠1+∠2=60°,那么∠3的度数是 ( )
A.150° B.120° C.60° D.30°
7. [2022成都外国语学校期中]如图,直线AB,CD相交于点O,射线OM平分∠AOC,如果∠AOD=104°,那么∠BOM的度数是 ( )
A.38° B.104° C.140° D.142°
8. 如图,直线AB,CD,EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
二、能力提升
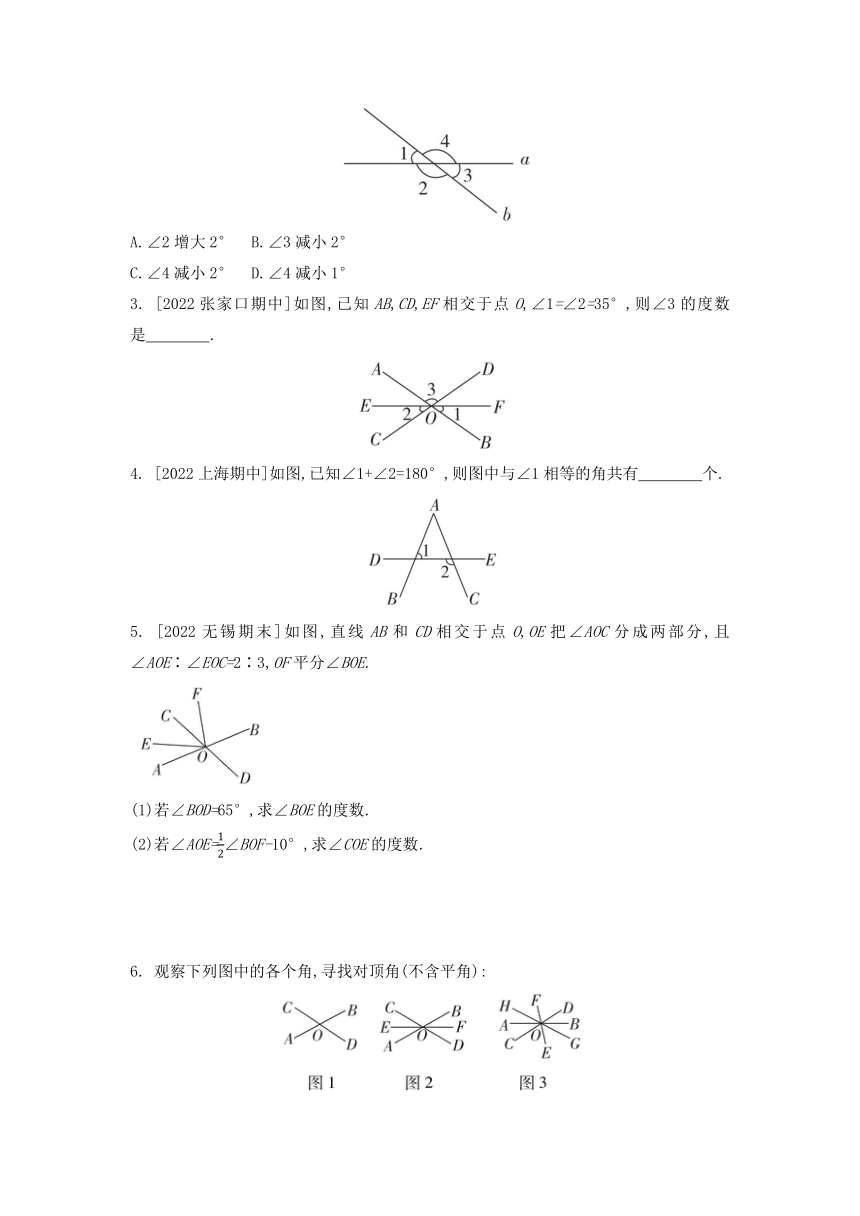
1. [2022晋中榆次区期中]如图,取两根木条a,b,将它们钉在一起,得到一个相交线的模型.转动木条,当∠1增大2°时,下列说法正确的是 ( )
A.∠2增大2° B.∠3减小2°
C.∠4减小2° D.∠4减小1°
3. [2022张家口期中]如图,已知AB,CD,EF相交于点O,∠1=∠2=35°,则∠3的度数是 .
4. [2022上海期中]如图,已知∠1+∠2=180°,则图中与∠1相等的角共有 个.
5. [2022无锡期末]如图,直线AB和CD相交于点O,OE把∠AOC分成两部分,且∠AOE∶∠EOC=2∶3,OF平分∠BOE.
(1)若∠BOD=65°,求∠BOE的度数.
(2)若∠AOE=∠BOF-10°,求∠COE的度数.
6. 观察下列图中的各个角,寻找对顶角(不含平角):
(1)如图1所示,两条直线AB与CD相交于一点形成 对对顶角.
(2)如图2所示,三条直线AB,CD,EF相交于一点形成 对对顶角.
(3)如图3所示,四条直线AB,CD,EF,GH相交于一点形成 对对顶角.
(4)探究(1)~(3)中直线条数与对顶角对数之间的关系,若有n(n≥2且n为整数)条直线相交于一点,则可形成多少对对顶角
参考答案
一、基础巩固
1. D
2. ∠2和∠4 45° 由题图可知,∠1的邻补角为∠2和∠4.因为∠1和∠2互为邻补角,所以∠1+∠2=180°,又∠1∶∠2=1∶3,所以∠1=180°×=45°.
3. B
4. A
5. D
6. A 根据对顶角的性质,可得∠1=∠2.因为∠1+∠2=60°,所以∠1=∠2=30°,所以∠3=180°-30°=150°.
7. D 解法一 因为∠AOD=104°,所以∠AOC=180°-104°=76°,∠BOC=∠AOD=104°.因为射线OM平分∠AOC,所以∠COM=∠AOC=38°,所以∠BOM=∠BOC+∠COM=104°+38°
=142°.
解法二 因为∠AOD=104°,所以∠AOC=180°-104°=76°.因为射线OM平分∠AOC,所以∠AOM=∠AOC=38°,所以∠BOM=180°-∠AOM=180°-38°=142°.
8. 解:(1)∠COE的邻补角为∠COF和∠EOD.
(2)∠COE和∠BOE的对顶角分别为∠DOF和∠AOF.
(3)因为∠BOF=90°,
所以∠AOF=180°-∠BOF=90°.
因为∠BOD=60°,所以∠AOC=∠BOD=60°,
所以∠FOC=∠AOF+∠AOC=90°+60°=150°.
二、能力提升
1. C 因为∠1与∠3是对顶角,所以∠1=∠3,所以当∠1增大2°时,∠3增大2°.因为∠1与∠2是邻补角,∠1与∠4是邻补角,所以∠1+∠2=180°,∠1+∠4=180°,所以当∠1增大2°时,∠2减小2°,∠4减小2°.故A,B,D错误,C正确.
2. C 因为∠AOC与∠BOD是对顶角,所以∠AOC=∠BOD=60°.因为∠AOC-2∠AOE=20°,所以∠AOE=20°.由题意可知,∠AOD=180°-∠BOD=120°,所以∠DOE=∠AOD-∠AOE=100°.因为射线OF平分∠DOE,所以∠DOF=∠DOE=50°,所以∠AOF=∠AOD-∠DOF=120°-50°=70°.
3. 110° 因为AB,CD,EF相交于点O,∠1=∠2=35°,所以∠BOC=180°-∠1-∠2=110°,又∠3与∠BOC是对顶角,所以∠3=∠BOC=110°.
4. 3 如图,因为∠1和∠3是对顶角,所以∠1=∠3.因为∠1+∠2=180°,∠2+∠4=180°,∠2+∠5=180°,所以∠1=∠4=∠5.综上,与∠1相等的角共有3个.
5. 解:(1)因为∠AOC与∠BOD是对顶角,
所以∠AOC=∠BOD=65°.
因为∠AOE∶∠EOC=2∶3,
所以∠AOE=∠AOC=26°.
所以∠BOE=180°-∠AOE=180°-26°=154°.
(2)设∠AOE=2x,∠EOC=3x.
因为∠AOE=∠BOF-10°,所以∠BOF=4x+20°.
因为OF平分∠BOE,
所以∠BOE=2∠BOF=8x+40°.
所以∠AOE+∠BOE=2x+8x+40°=180°,所以x=14°,
所以∠COE=3x=42°.
6. 解:(1)2
(2)6
直线AB与CD相交形成2对对顶角,直线AB与EF相交形成2对对顶角,直线CD与EF相交形成2对对顶角,故共有6对对顶角.
(3)12
直线AB与CD相交形成2对对顶角,直线AB与EF相交形成2对对顶角,直线AB与GH相交形成2对对顶角,直线CD与EF相交形成2对对顶角,直线CD与GH相交形成2对对顶角,直线EF与GH相交形成2对对顶角,故共有12对对顶角.
(4)根据(1)~(3)中的结论,可知n条直线相交于一点可形成n(n-1)对对顶角.
(课时1 相交线)
一、基础巩固
知识点1 邻补角的定义与性质
1. [2022重庆荣昌区期末]下列各图中,∠1与∠2是邻补角的是 ( )
2. 如图,直线AB,CD相交所成的四个角中,∠1的邻补角为 ,若∠1∶∠2=1∶3,则∠1的度数为 .
知识点2 对顶角的定义与性质
3. [2022秦皇岛期中]下列各图中,∠1与∠2是对顶角的是 ( )
4. [2022北京中考]如图,利用工具测量角,则∠1的大小为 ( )
A.30° B.60° C.120° D.150°
5. 如图,直线AB与CD相交于点O,若∠AOC=75°,∠1=25°,则∠2的度数是 ( )
A.25° B.30° C.40° D.50°
知识点3 邻补角与对顶角的综合应用
6. 王麻子剪刀是北京市的传统工艺品,其锻制技艺被国务院列入第二批国家级非物质文化遗产名录,如图1是王麻子剪刀,把它抽象为图2所示,如果∠1+∠2=60°,那么∠3的度数是 ( )
A.150° B.120° C.60° D.30°
7. [2022成都外国语学校期中]如图,直线AB,CD相交于点O,射线OM平分∠AOC,如果∠AOD=104°,那么∠BOM的度数是 ( )
A.38° B.104° C.140° D.142°
8. 如图,直线AB,CD,EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
二、能力提升
1. [2022晋中榆次区期中]如图,取两根木条a,b,将它们钉在一起,得到一个相交线的模型.转动木条,当∠1增大2°时,下列说法正确的是 ( )
A.∠2增大2° B.∠3减小2°
C.∠4减小2° D.∠4减小1°
3. [2022张家口期中]如图,已知AB,CD,EF相交于点O,∠1=∠2=35°,则∠3的度数是 .
4. [2022上海期中]如图,已知∠1+∠2=180°,则图中与∠1相等的角共有 个.
5. [2022无锡期末]如图,直线AB和CD相交于点O,OE把∠AOC分成两部分,且∠AOE∶∠EOC=2∶3,OF平分∠BOE.
(1)若∠BOD=65°,求∠BOE的度数.
(2)若∠AOE=∠BOF-10°,求∠COE的度数.
6. 观察下列图中的各个角,寻找对顶角(不含平角):
(1)如图1所示,两条直线AB与CD相交于一点形成 对对顶角.
(2)如图2所示,三条直线AB,CD,EF相交于一点形成 对对顶角.
(3)如图3所示,四条直线AB,CD,EF,GH相交于一点形成 对对顶角.
(4)探究(1)~(3)中直线条数与对顶角对数之间的关系,若有n(n≥2且n为整数)条直线相交于一点,则可形成多少对对顶角
参考答案
一、基础巩固
1. D
2. ∠2和∠4 45° 由题图可知,∠1的邻补角为∠2和∠4.因为∠1和∠2互为邻补角,所以∠1+∠2=180°,又∠1∶∠2=1∶3,所以∠1=180°×=45°.
3. B
4. A
5. D
6. A 根据对顶角的性质,可得∠1=∠2.因为∠1+∠2=60°,所以∠1=∠2=30°,所以∠3=180°-30°=150°.
7. D 解法一 因为∠AOD=104°,所以∠AOC=180°-104°=76°,∠BOC=∠AOD=104°.因为射线OM平分∠AOC,所以∠COM=∠AOC=38°,所以∠BOM=∠BOC+∠COM=104°+38°
=142°.
解法二 因为∠AOD=104°,所以∠AOC=180°-104°=76°.因为射线OM平分∠AOC,所以∠AOM=∠AOC=38°,所以∠BOM=180°-∠AOM=180°-38°=142°.
8. 解:(1)∠COE的邻补角为∠COF和∠EOD.
(2)∠COE和∠BOE的对顶角分别为∠DOF和∠AOF.
(3)因为∠BOF=90°,
所以∠AOF=180°-∠BOF=90°.
因为∠BOD=60°,所以∠AOC=∠BOD=60°,
所以∠FOC=∠AOF+∠AOC=90°+60°=150°.
二、能力提升
1. C 因为∠1与∠3是对顶角,所以∠1=∠3,所以当∠1增大2°时,∠3增大2°.因为∠1与∠2是邻补角,∠1与∠4是邻补角,所以∠1+∠2=180°,∠1+∠4=180°,所以当∠1增大2°时,∠2减小2°,∠4减小2°.故A,B,D错误,C正确.
2. C 因为∠AOC与∠BOD是对顶角,所以∠AOC=∠BOD=60°.因为∠AOC-2∠AOE=20°,所以∠AOE=20°.由题意可知,∠AOD=180°-∠BOD=120°,所以∠DOE=∠AOD-∠AOE=100°.因为射线OF平分∠DOE,所以∠DOF=∠DOE=50°,所以∠AOF=∠AOD-∠DOF=120°-50°=70°.
3. 110° 因为AB,CD,EF相交于点O,∠1=∠2=35°,所以∠BOC=180°-∠1-∠2=110°,又∠3与∠BOC是对顶角,所以∠3=∠BOC=110°.
4. 3 如图,因为∠1和∠3是对顶角,所以∠1=∠3.因为∠1+∠2=180°,∠2+∠4=180°,∠2+∠5=180°,所以∠1=∠4=∠5.综上,与∠1相等的角共有3个.
5. 解:(1)因为∠AOC与∠BOD是对顶角,
所以∠AOC=∠BOD=65°.
因为∠AOE∶∠EOC=2∶3,
所以∠AOE=∠AOC=26°.
所以∠BOE=180°-∠AOE=180°-26°=154°.
(2)设∠AOE=2x,∠EOC=3x.
因为∠AOE=∠BOF-10°,所以∠BOF=4x+20°.
因为OF平分∠BOE,
所以∠BOE=2∠BOF=8x+40°.
所以∠AOE+∠BOE=2x+8x+40°=180°,所以x=14°,
所以∠COE=3x=42°.
6. 解:(1)2
(2)6
直线AB与CD相交形成2对对顶角,直线AB与EF相交形成2对对顶角,直线CD与EF相交形成2对对顶角,故共有6对对顶角.
(3)12
直线AB与CD相交形成2对对顶角,直线AB与EF相交形成2对对顶角,直线AB与GH相交形成2对对顶角,直线CD与EF相交形成2对对顶角,直线CD与GH相交形成2对对顶角,直线EF与GH相交形成2对对顶角,故共有12对对顶角.
(4)根据(1)~(3)中的结论,可知n条直线相交于一点可形成n(n-1)对对顶角.
