高二物理粤教版(2019)选择必修二 1.3洛伦兹力 课时作业(含解析)
文档属性
| 名称 | 高二物理粤教版(2019)选择必修二 1.3洛伦兹力 课时作业(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 1000.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-03-22 13:01:57 | ||
图片预览




文档简介
1.3洛伦兹力
一、单选题
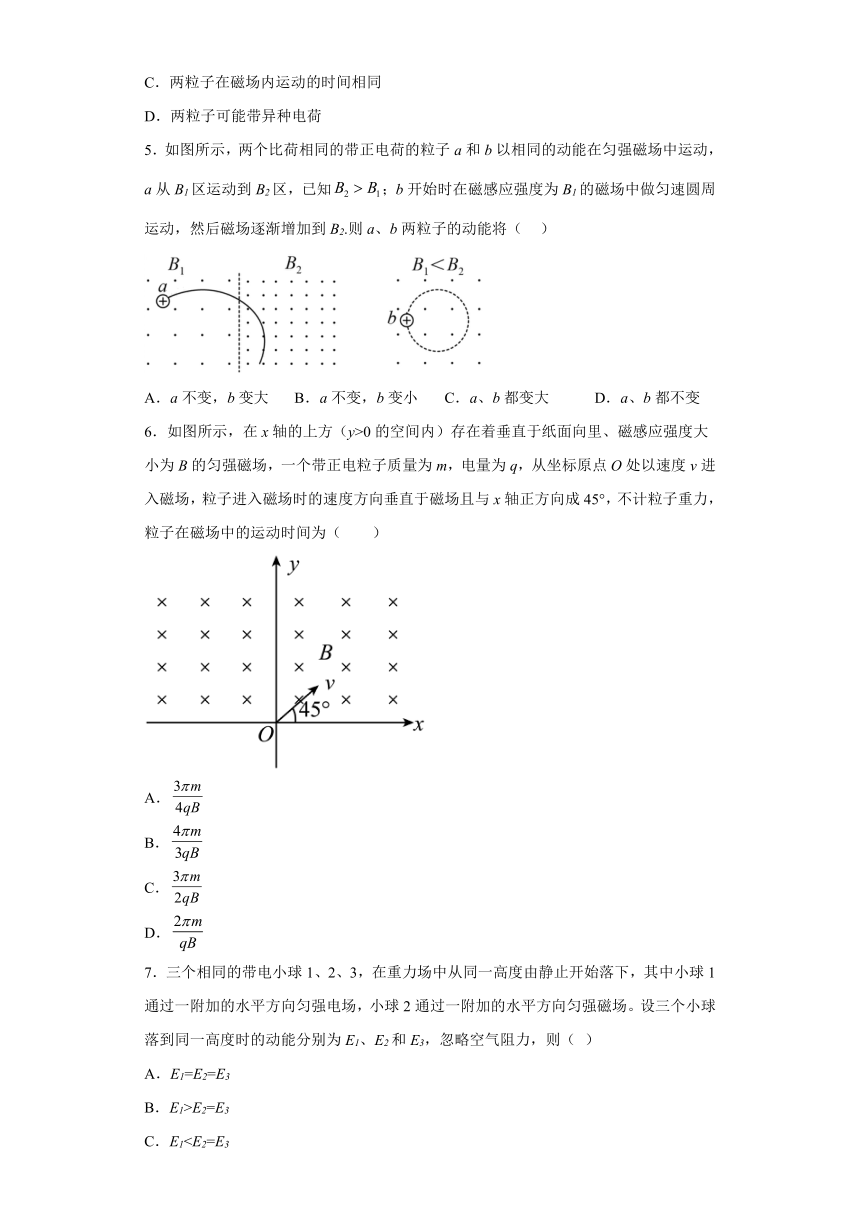
1.如图所示,运动电荷在磁场中没有受到洛伦兹力的是 ( )
A. B.
C. D.
2.如图所示,匀强磁场方向垂直纸面向里,一带负电的粒子(不计重力)由右方垂直磁场方向射入磁场中,在匀强磁场的作用下将向哪个方向偏转( )
A.向上 B.向下 C.向里 D.向外
3.带电粒子、在同一匀强磁场中做匀速圆周运动,他们的动量大小相等,运动的半径大于运动的半径。若、的电荷量分别为、,质量分别为、,周期分别为、,则一定有( )
A. B. C. D.
4.如图,边界MN下方是一垂直纸面向里的匀强磁场,甲、乙两带电粒子先后从c点沿与MN成45°角的方向射入磁场,最后都从d点射出磁场,已知,,不计重力,则( )
A.两粒子的速率相同
B.两粒子的动能相同
C.两粒子在磁场内运动的时间相同
D.两粒子可能带异种电荷
5.如图所示,两个比荷相同的带正电荷的粒子a和b以相同的动能在匀强磁场中运动,a从B1区运动到B2区,已知;b开始时在磁感应强度为B1的磁场中做匀速圆周运动,然后磁场逐渐增加到B2.则a、b两粒子的动能将( )
A.a不变,b变大 B.a不变,b变小 C.a、b都变大 D.a、b都不变
6.如图所示,在x轴的上方(y>0的空间内)存在着垂直于纸面向里、磁感应强度大小为B的匀强磁场,一个带正电粒子质量为m,电量为q,从坐标原点O处以速度v进入磁场,粒子进入磁场时的速度方向垂直于磁场且与x轴正方向成45°,不计粒子重力,粒子在磁场中的运动时间为( )
A.
B.
C.
D.
7.三个相同的带电小球1、2、3,在重力场中从同一高度由静止开始落下,其中小球1通过一附加的水平方向匀强电场,小球2通过一附加的水平方向匀强磁场。设三个小球落到同一高度时的动能分别为E1、E2和E3,忽略空气阻力,则( )
A.E1=E2=E3
B.E1>E2=E3
C.E1D.E1>E2>E3
8.如图所示,匀强磁场限定在一个圆形区域内,磁场方向垂直纸面向外,一个质量为,电荷量为,初速度大小为的带电粒子沿磁场区域的直径方向从点射入磁场,从点沿半径方向射出磁场,粒子射出磁场时的速度方向与射入磁场时相比偏转了角,忽略重力及粒子间的相互作用力。根据题中信息( )
A.可以判定粒子的电性
B.可求得粒子在磁场中运动的轨迹长度
C.可求得磁场的磁感应强度
D.可求得粒子在磁场中运动的时间
二、多选题
9.下列说法正确的是( )
A.奥斯特首先发现了电流的磁效应
B.安培发明了电流产生的磁场的方向的判定方法
C.安培首先提出了分子电流假说
D.安培首先提出了磁场对运动电荷有力作用
10.如图所示,在以R为半径、O为圆心的圆形区域内存在磁场,直径PQ左侧区域存在一方向垂直于纸面向里、磁感应强度大小为B1的匀强磁场;PQ右侧区域存在一方向垂直于纸面向外、磁感应强度大小为B2的匀强磁场.现有一质量为m、电荷量为q的带负电粒子(不计重力)从C点沿垂直于PQ的方向射入磁场,并仅通过PQ—次,最终从D点离开磁场,离开磁场时粒子的运动方向仍垂直于PQ.图中CE与DF均垂直于PQ,EF=R.已知OC与PQ的夹角为θ1=30°,OD与PQ的夹角为θ2,粒子在PQ左侧和右侧磁场区域中的运动时间分别为t1和t2,则以下说法中正确的是
A.θ2=60° B. C. D.
11.如图所示,在x≥0,y≥0的空间中有恒定的匀强磁场,磁感应强度的方向垂直于xOy平面向里,大小为B。现有一质量为m、电荷量为q的带正电粒子,从x轴上的某点P沿着与x轴成30°角的方向射入磁场。不计重力的影响,则下列说法正确的是( )
A.只要粒子的速率合适,粒子就可能通过坐标原点
B.粒子在磁场中运动所经历的时间可能为
C.粒子在磁场中运动所经历的时间可能为
D.粒子在磁场中运动所经历的时间可能为
12.如图所示,直角三角形ABC中存在一匀强磁场,比荷相同的两粒子沿AB方向从A点射入磁场,分别从AC边上的P、Q两点射出。下列说法正确的是( )
A.从Q点射出的粒子速度较大
B.从Q点射出的粒子在磁场中运动的周期大
C.从Q点射出的粒子,在磁场中运动的时间长
D.两粒子在磁场中运动的时间一样长
三、解答题
13.如图所示,真空中有直角坐标系xOy,P(a,-b)是坐标系中的一个点,a、b是大于0的常数。在的区域内存在者垂直于xOy平面的匀强磁场。一质量为m、电荷量为q的带正电粒子从坐标原点O以速度v0沿y轴正方向射入磁场。离开磁场后恰好通过P点。不计粒子的重力,求:
(1)磁感应强度B的大小和方向:
(2)粒子从O点运动到P点的时间t。
14.一个质量为m电荷量为q的带电粒子,从x轴上的点以速度v,沿与x正方向成的方向射入第一象限内的匀强磁场中,并恰好垂直于y轴射出第一象限,不计重力。求:
(1)匀强磁场的磁感应强度的大小;
(2)带电粒子在第一象限运动的时间。
15.如图所示,在直角坐标系中,轴上方有匀强磁场,磁感应强度的大小为,磁场方向垂直于纸面向外。在坐标原点处有一个放射源,可沿纸面向各方向射出速率均为的粒子,已知粒子的质量,电量。
(1)粒子在磁场中运动的半径和周期。
(2)坐标为(20cm,0)点有两个粒子能够打到,求两个粒子到达的时间差。
(3)如果粒子只射向第二象限(包括坐标轴),画出粒子能到达区域的大致图像,并求出面积?
参考答案:
1.D
【详解】电荷在磁场中运动的方向与磁场平行时,不受洛伦兹力的作用,不平行时受洛伦兹力。
故选D。
2.A
【详解】粒子带负电,向左移动,根据左手定则,洛伦兹力向上,故带电粒子向上偏转且做圆周运动。
故选A。
3.A
【详解】根据洛伦兹力提供向心力,有
可得
依题意知,,,则一定有
由于两粒子的速度大小关系未知,所以利用题目已知条件无法确定二者质量大小关系,从而无法确定二者的比荷()大小关系,以及两粒子在磁场中运动的周期大小关系。
故选A。
4.B
【详解】ABD.由题意作出粒子运动轨迹如图所示
由左手定则可知,两粒子均带正电,由几何关系可知,两粒子的运动半径相同,则根据洛伦兹力充当向心力可得
解得
则动能
将,,代入可得,两粒子的速率不相同,但动能相等,故AD错误,B正确;
C.粒子转动周期
圆心角为,则粒子在磁场内运动的时间
将,,代入可得,两粒子在磁场内运动的时间不相同,故C错误。
故选B。
5.A
【详解】ABCD.a粒子一直在恒定的磁场中运动,受到的洛伦兹力不做功,动能不变;b粒子在变化的磁场中运动,由于变化的磁场要产生感生电场,感生电场会对它做正功,使其动能变大,故A正确BCD错误。
故选A。
6.C
【详解】根据单边有界磁场的的对称性可知,粒子进入磁场时速度与x轴的夹角为45°角,穿出磁场时与x轴的夹角仍为45°角,根据左手定则可知,粒子沿逆时针方向旋转,作轨迹如图所示
由几何关系可知,速度的偏向角为270°角,轨道对应的圆心角也为270°,粒子圆周运动的周期为
故粒子在磁场中运动的时间
故选C。
7.B
【详解】洛伦兹力方向与速度方向时刻是垂直关系的,即洛伦兹力对粒子不做功,小球1在运动过程中,重力、电场力对其做正功,小球2和小球3在运动过程中只有重力做功,而三个小球从同一高度释放,下落到同一高度,所以重力做功相同,故
ACD错误,B正确。
故选B。
8.A
【详解】A.根据粒子的偏转方向,由左手定则可以判断出粒子带正电,A正确;
B.由洛伦兹力提供向心力可得
解得粒子在磁场中运动时,其轨迹的半径为
由几何关系可知其对应的圆心角为,则粒子在磁场中运动的轨迹长度为
因为不知道磁场的磁场强度,不可求得粒子在磁场中运动的轨迹长度,B错误;
C. 粒子在磁场中运动时,有
由于不知道粒子的半径,故不可求得磁场的磁感应强度,C错误。
D.粒子做匀速运动的周期为
则粒子在磁场中运动的时间为
因为不知道磁场的磁场强度,不可求得粒子在磁场中运动的时间,D错误。
故选A。
9.ABC
【详解】A.奥斯特首先发现了电流的磁效应。故A正确;
B.安培发现了电流产生的磁场的方向的判定方法,即安培定则。故B正确;
C.安培首先提出了分子电流假说。故C正确;
D.洛伦兹首先提出了磁场对运动电荷有力作用。故D错误。
故选ABC。
10.ABC
【详解】AB.由几何知识可知,,故,故,粒子运动轨迹如图所示:
根据几何知识可得,又知道,解得,AB正确;
CD.粒子在磁场中做匀速圆周运动的周期,根据几何知识可得两轨迹所对圆心角相等,粒子在磁场中的运动时间都为,故,故D错误,C正确.
故选ABC。
11.BC
【详解】A.带正电粒子由P点沿与x轴成30°角的方向入射,则粒子运动轨迹的圆心在过P点且与速度方向垂直的方向上,粒子在磁场中要想到达坐标原点,转过的圆心角肯定大于180°,如图所示。而因磁场有边界,故粒子不可能通过坐标原点,故A错误;
BCD.由于P点的位置不定,所以粒子在磁场中的轨迹圆弧对应的圆心角也不同,最大的圆心角为300°,运动的时间
t=T=
当粒子从无限靠近坐标原点出发时,对应的最小圆心角也一定大于120°,所以运动时间
t>T=
故粒子在磁场中运动的时间范围是
故BC正确D错误。
故选BC。
12.AD
【详解】A.两带电粒子在磁场中运动轨迹如图所示
由图看出,从Q点射出的粒子半径大,根据
可得
则从Q点射出的粒子速度大,A正确;
B.粒子在磁场中运动的周期为
可见粒子两粒子周期相同,B错误;
CD.如上图,设粒子运动轨迹圆心分别为O1、O2,弦AP、AQ的中垂线交AC于M点和N点,由于∠AO1M=∠AO2N,所以∠MO1P=∠NO2Q,即两粒子轨迹所对的圆心角相等,又因为两粒子周期相同,由
可知两粒子在磁场中运动时间一样长,D正确,C错误。
故选AD。
13.(1),垂直纸面向外;(2)
【详解】(1)粒子在第一象限做圆周运动,在第四象限做直线运动。由左手定则得B的方向垂直纸面向外。
由几何关系得
由洛伦兹力提供向心力得
解得
(2)粒子在磁场中运动时间为
在第四象限运动时间为
总时间为
14.(1);(2)
【详解】(1)粒子在磁场中的运动轨迹如图所示
由几何关系可知
rsin30°=l
由洛伦兹力提供向心力可得
联立解得
(2)由图像可知,粒子运动对应的圆心角为θ=150°,根据
,
解得
15.(1),;(2);(3) ,0.166m2
【详解】(1)根据
可得粒子运动的轨道半径
根据
可得
(2)从第一象限内射出的粒子速度方向与x轴正向夹角为30°,此时粒子在磁场中运动圆心角为60°,则打到该点的时间
同理,从第二象限内射出打到的时间
时间差为
(3)如图所示。面积为
一、单选题
1.如图所示,运动电荷在磁场中没有受到洛伦兹力的是 ( )
A. B.
C. D.
2.如图所示,匀强磁场方向垂直纸面向里,一带负电的粒子(不计重力)由右方垂直磁场方向射入磁场中,在匀强磁场的作用下将向哪个方向偏转( )
A.向上 B.向下 C.向里 D.向外
3.带电粒子、在同一匀强磁场中做匀速圆周运动,他们的动量大小相等,运动的半径大于运动的半径。若、的电荷量分别为、,质量分别为、,周期分别为、,则一定有( )
A. B. C. D.
4.如图,边界MN下方是一垂直纸面向里的匀强磁场,甲、乙两带电粒子先后从c点沿与MN成45°角的方向射入磁场,最后都从d点射出磁场,已知,,不计重力,则( )
A.两粒子的速率相同
B.两粒子的动能相同
C.两粒子在磁场内运动的时间相同
D.两粒子可能带异种电荷
5.如图所示,两个比荷相同的带正电荷的粒子a和b以相同的动能在匀强磁场中运动,a从B1区运动到B2区,已知;b开始时在磁感应强度为B1的磁场中做匀速圆周运动,然后磁场逐渐增加到B2.则a、b两粒子的动能将( )
A.a不变,b变大 B.a不变,b变小 C.a、b都变大 D.a、b都不变
6.如图所示,在x轴的上方(y>0的空间内)存在着垂直于纸面向里、磁感应强度大小为B的匀强磁场,一个带正电粒子质量为m,电量为q,从坐标原点O处以速度v进入磁场,粒子进入磁场时的速度方向垂直于磁场且与x轴正方向成45°,不计粒子重力,粒子在磁场中的运动时间为( )
A.
B.
C.
D.
7.三个相同的带电小球1、2、3,在重力场中从同一高度由静止开始落下,其中小球1通过一附加的水平方向匀强电场,小球2通过一附加的水平方向匀强磁场。设三个小球落到同一高度时的动能分别为E1、E2和E3,忽略空气阻力,则( )
A.E1=E2=E3
B.E1>E2=E3
C.E1
8.如图所示,匀强磁场限定在一个圆形区域内,磁场方向垂直纸面向外,一个质量为,电荷量为,初速度大小为的带电粒子沿磁场区域的直径方向从点射入磁场,从点沿半径方向射出磁场,粒子射出磁场时的速度方向与射入磁场时相比偏转了角,忽略重力及粒子间的相互作用力。根据题中信息( )
A.可以判定粒子的电性
B.可求得粒子在磁场中运动的轨迹长度
C.可求得磁场的磁感应强度
D.可求得粒子在磁场中运动的时间
二、多选题
9.下列说法正确的是( )
A.奥斯特首先发现了电流的磁效应
B.安培发明了电流产生的磁场的方向的判定方法
C.安培首先提出了分子电流假说
D.安培首先提出了磁场对运动电荷有力作用
10.如图所示,在以R为半径、O为圆心的圆形区域内存在磁场,直径PQ左侧区域存在一方向垂直于纸面向里、磁感应强度大小为B1的匀强磁场;PQ右侧区域存在一方向垂直于纸面向外、磁感应强度大小为B2的匀强磁场.现有一质量为m、电荷量为q的带负电粒子(不计重力)从C点沿垂直于PQ的方向射入磁场,并仅通过PQ—次,最终从D点离开磁场,离开磁场时粒子的运动方向仍垂直于PQ.图中CE与DF均垂直于PQ,EF=R.已知OC与PQ的夹角为θ1=30°,OD与PQ的夹角为θ2,粒子在PQ左侧和右侧磁场区域中的运动时间分别为t1和t2,则以下说法中正确的是
A.θ2=60° B. C. D.
11.如图所示,在x≥0,y≥0的空间中有恒定的匀强磁场,磁感应强度的方向垂直于xOy平面向里,大小为B。现有一质量为m、电荷量为q的带正电粒子,从x轴上的某点P沿着与x轴成30°角的方向射入磁场。不计重力的影响,则下列说法正确的是( )
A.只要粒子的速率合适,粒子就可能通过坐标原点
B.粒子在磁场中运动所经历的时间可能为
C.粒子在磁场中运动所经历的时间可能为
D.粒子在磁场中运动所经历的时间可能为
12.如图所示,直角三角形ABC中存在一匀强磁场,比荷相同的两粒子沿AB方向从A点射入磁场,分别从AC边上的P、Q两点射出。下列说法正确的是( )
A.从Q点射出的粒子速度较大
B.从Q点射出的粒子在磁场中运动的周期大
C.从Q点射出的粒子,在磁场中运动的时间长
D.两粒子在磁场中运动的时间一样长
三、解答题
13.如图所示,真空中有直角坐标系xOy,P(a,-b)是坐标系中的一个点,a、b是大于0的常数。在的区域内存在者垂直于xOy平面的匀强磁场。一质量为m、电荷量为q的带正电粒子从坐标原点O以速度v0沿y轴正方向射入磁场。离开磁场后恰好通过P点。不计粒子的重力,求:
(1)磁感应强度B的大小和方向:
(2)粒子从O点运动到P点的时间t。
14.一个质量为m电荷量为q的带电粒子,从x轴上的点以速度v,沿与x正方向成的方向射入第一象限内的匀强磁场中,并恰好垂直于y轴射出第一象限,不计重力。求:
(1)匀强磁场的磁感应强度的大小;
(2)带电粒子在第一象限运动的时间。
15.如图所示,在直角坐标系中,轴上方有匀强磁场,磁感应强度的大小为,磁场方向垂直于纸面向外。在坐标原点处有一个放射源,可沿纸面向各方向射出速率均为的粒子,已知粒子的质量,电量。
(1)粒子在磁场中运动的半径和周期。
(2)坐标为(20cm,0)点有两个粒子能够打到,求两个粒子到达的时间差。
(3)如果粒子只射向第二象限(包括坐标轴),画出粒子能到达区域的大致图像,并求出面积?
参考答案:
1.D
【详解】电荷在磁场中运动的方向与磁场平行时,不受洛伦兹力的作用,不平行时受洛伦兹力。
故选D。
2.A
【详解】粒子带负电,向左移动,根据左手定则,洛伦兹力向上,故带电粒子向上偏转且做圆周运动。
故选A。
3.A
【详解】根据洛伦兹力提供向心力,有
可得
依题意知,,,则一定有
由于两粒子的速度大小关系未知,所以利用题目已知条件无法确定二者质量大小关系,从而无法确定二者的比荷()大小关系,以及两粒子在磁场中运动的周期大小关系。
故选A。
4.B
【详解】ABD.由题意作出粒子运动轨迹如图所示
由左手定则可知,两粒子均带正电,由几何关系可知,两粒子的运动半径相同,则根据洛伦兹力充当向心力可得
解得
则动能
将,,代入可得,两粒子的速率不相同,但动能相等,故AD错误,B正确;
C.粒子转动周期
圆心角为,则粒子在磁场内运动的时间
将,,代入可得,两粒子在磁场内运动的时间不相同,故C错误。
故选B。
5.A
【详解】ABCD.a粒子一直在恒定的磁场中运动,受到的洛伦兹力不做功,动能不变;b粒子在变化的磁场中运动,由于变化的磁场要产生感生电场,感生电场会对它做正功,使其动能变大,故A正确BCD错误。
故选A。
6.C
【详解】根据单边有界磁场的的对称性可知,粒子进入磁场时速度与x轴的夹角为45°角,穿出磁场时与x轴的夹角仍为45°角,根据左手定则可知,粒子沿逆时针方向旋转,作轨迹如图所示
由几何关系可知,速度的偏向角为270°角,轨道对应的圆心角也为270°,粒子圆周运动的周期为
故粒子在磁场中运动的时间
故选C。
7.B
【详解】洛伦兹力方向与速度方向时刻是垂直关系的,即洛伦兹力对粒子不做功,小球1在运动过程中,重力、电场力对其做正功,小球2和小球3在运动过程中只有重力做功,而三个小球从同一高度释放,下落到同一高度,所以重力做功相同,故
ACD错误,B正确。
故选B。
8.A
【详解】A.根据粒子的偏转方向,由左手定则可以判断出粒子带正电,A正确;
B.由洛伦兹力提供向心力可得
解得粒子在磁场中运动时,其轨迹的半径为
由几何关系可知其对应的圆心角为,则粒子在磁场中运动的轨迹长度为
因为不知道磁场的磁场强度,不可求得粒子在磁场中运动的轨迹长度,B错误;
C. 粒子在磁场中运动时,有
由于不知道粒子的半径,故不可求得磁场的磁感应强度,C错误。
D.粒子做匀速运动的周期为
则粒子在磁场中运动的时间为
因为不知道磁场的磁场强度,不可求得粒子在磁场中运动的时间,D错误。
故选A。
9.ABC
【详解】A.奥斯特首先发现了电流的磁效应。故A正确;
B.安培发现了电流产生的磁场的方向的判定方法,即安培定则。故B正确;
C.安培首先提出了分子电流假说。故C正确;
D.洛伦兹首先提出了磁场对运动电荷有力作用。故D错误。
故选ABC。
10.ABC
【详解】AB.由几何知识可知,,故,故,粒子运动轨迹如图所示:
根据几何知识可得,又知道,解得,AB正确;
CD.粒子在磁场中做匀速圆周运动的周期,根据几何知识可得两轨迹所对圆心角相等,粒子在磁场中的运动时间都为,故,故D错误,C正确.
故选ABC。
11.BC
【详解】A.带正电粒子由P点沿与x轴成30°角的方向入射,则粒子运动轨迹的圆心在过P点且与速度方向垂直的方向上,粒子在磁场中要想到达坐标原点,转过的圆心角肯定大于180°,如图所示。而因磁场有边界,故粒子不可能通过坐标原点,故A错误;
BCD.由于P点的位置不定,所以粒子在磁场中的轨迹圆弧对应的圆心角也不同,最大的圆心角为300°,运动的时间
t=T=
当粒子从无限靠近坐标原点出发时,对应的最小圆心角也一定大于120°,所以运动时间
t>T=
故粒子在磁场中运动的时间范围是
故选BC。
12.AD
【详解】A.两带电粒子在磁场中运动轨迹如图所示
由图看出,从Q点射出的粒子半径大,根据
可得
则从Q点射出的粒子速度大,A正确;
B.粒子在磁场中运动的周期为
可见粒子两粒子周期相同,B错误;
CD.如上图,设粒子运动轨迹圆心分别为O1、O2,弦AP、AQ的中垂线交AC于M点和N点,由于∠AO1M=∠AO2N,所以∠MO1P=∠NO2Q,即两粒子轨迹所对的圆心角相等,又因为两粒子周期相同,由
可知两粒子在磁场中运动时间一样长,D正确,C错误。
故选AD。
13.(1),垂直纸面向外;(2)
【详解】(1)粒子在第一象限做圆周运动,在第四象限做直线运动。由左手定则得B的方向垂直纸面向外。
由几何关系得
由洛伦兹力提供向心力得
解得
(2)粒子在磁场中运动时间为
在第四象限运动时间为
总时间为
14.(1);(2)
【详解】(1)粒子在磁场中的运动轨迹如图所示
由几何关系可知
rsin30°=l
由洛伦兹力提供向心力可得
联立解得
(2)由图像可知,粒子运动对应的圆心角为θ=150°,根据
,
解得
15.(1),;(2);(3) ,0.166m2
【详解】(1)根据
可得粒子运动的轨道半径
根据
可得
(2)从第一象限内射出的粒子速度方向与x轴正向夹角为30°,此时粒子在磁场中运动圆心角为60°,则打到该点的时间
同理,从第二象限内射出打到的时间
时间差为
(3)如图所示。面积为
同课章节目录
- 第一章 磁场
- 第一节 安培力
- 第二节 安培力的应用
- 第三节 洛伦兹力
- 第四节 洛伦兹力与现代技术
- 第二章 电磁感应
- 第一节 感应电流的方向
- 第二节 法拉第电磁感应定律
- 第三节 电磁感应定律的应用
- 第四节 互感和自感
- 第五节 涡流现象及其应用
- 第三章 交变电流
- 第一节 认识交变电流
- 第二节 描述交变电流的物理量
- 第三节 变压器
- 第四节 远距离输电
- 第四章 电磁震荡与电磁波
- 第一节 电磁振动
- 第二节 麦克斯韦电磁电磁场理论
- 第三节 电磁波的发射、传播和接收
- 第四节 电磁波谱
- 第五章 传感器
- 第一节 传感器及其工作原理
- 第二节 传感器的应用
- 第三节 用传感器制作自动控制装置
- 第四节 利用智能手机中的磁传感器研究磁现象
