【新课标】4.3.1公式法 课件(共20张PPT)
文档属性
| 名称 | 【新课标】4.3.1公式法 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 17:55:45 | ||
图片预览








文档简介
(共20张PPT)
4.3.1公式法
北师版八年级下册
教学目标
1、探究能用平方差公式进行因式分解的多项式的特点;
2、会用平方差公式进行分解因式;
3、会综合运用提公因式法和平方差公式法分解因式.
新知导入
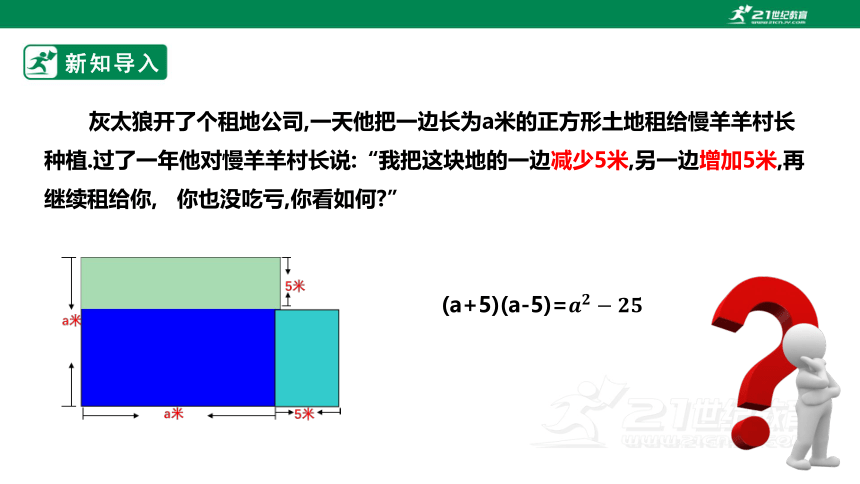
灰太狼开了个租地公司,一天他把一边长为a米的正方形土地租给慢羊羊村长种植.过了一年他对慢羊羊村长说:“我把这块地的一边减少5米,另一边增加5米,再继续租给你, 你也没吃亏,你看如何 ”
(a+5)(a-5)=
新知讲解
想一想:多项式x2-25, 9x2-y2能用提公因式法分解因式吗?如果不能,你有其他方法将它分解因式吗?
(1)观察多项式 x2-25 和 9x2-y2,它们有什么共同特征?
(2)尝试将它们分别写成两个因式的乘积.
多项式x2-25和9x2-y2都可以写成两个式子的平方差的形式:
x2-25=x2-52, 9x2-y2 =(3x)2-y2
把乘法公式(a+b)(a-b)=a2-b2反过来,就得到a2-b2=(a+b)(a-b),于是有:
x2-25=x2-52=(x+5)(x-5);
9x2-y2 =(3x)2-y2=(3x+y)(3x-y).
新知讲解
=(a+b)(a-b)
因式分解
两个数的平方差,等于这两个数的和与这两个数的差的乘积.
平方差公式:
你能用自己的语言描述这个公式吗?
新知讲解
1.多项式有两项;
2.这两项能写成平方差的形式,
即能写成:( )2-( )2的形式.
思考:一个多项式具备哪些特点才可以用平方差公式分解因式?
典例精析
例1 把下列各式因式分解:
(1)25-16x2; (2)9a2- b2.
解:(1) 25-16x2= 52-(4x)2=(5+4x)(5-4x);
(2)9a2-b2= (3a)2-(b)2=(3a+b)(3a-b)
归纳总结
利用平方差公式分解两项式的一般步骤:
1. 找出公式中的a、b;
2. 转化成a 2-b 2的形式;
3. 根据公式a 2-b 2=(a+b) (a-b) 写出结果.
典例精析
例2 把下列各式因式分解:
(1)9(m+n)2-(m-n)2; (2) 2x3-8x.
解:(1) 9(m+n)2-(m-n)2 =[3(m+n)]2-(m-n)2
= [3(m+n)+(m-n)] [3(m+n)-(m-n)]
= (3m+3n+m-n)(3m+3n-m+n)
=(4m+2n)(2m+4n)
=4(2m+n)(m+2n);
(2)2x3-8x=2x(x2-4) = 2x(x2-22) =2x (x+2)(x-2)
当多项式的各项含有公因式时,通常先提出这个公因式,然后再进一步因式分解
归纳总结
1.具有平方差形式的多项式才可运用平方差公式分解因式.
2.公式中的字母 可以是单项式,也可以是多项式,应视具体情形灵活运用.
3.公式中的a、b可以代表多项式,此时我们将多项式看成整体套用公式,改写平方形式时不要漏掉系数;
4.若多项式中有公因式,应先提取公因式,然后再进一步分解因式.
5.分解因式要彻底.要注意每一个因式的形式要最简,直到不能再分解为止.
课堂练习
1、把x 3-9x 分解因式,结果正确的是( )
A.x (x 2-9) B.x (x-3)2
C.x (x+3)2 D.x (x+3)(x-3)
D
2、一次课堂练习,小颖同学做了以下几道因式分解题,你认为她做得不够完整的是( )
A.x 3-x=x (x 2-1)
B.x 2y-y 3=y (x+y )(x-y )
C.-m 2+4n 2=(2n+m)(2n-m)
D.3p 2-27q 2=3( p+3q )( p-3q )
A
课堂练习
3、已知|x-y+2|+=0,
则x 2-y 2的值为________.
4、若x 2-9=(x-3)(x+a),则a=________.
5、已知a+b=3,a-b=5,则式子a 2-b 2的值是________.
-4
3
15
课堂练习
6、把下列各式分解因式:
(1)(3a-2b)2-(2a+3b)2; (2)x 4-81y 4;
(3)a 4-9a 2b 2; (4)m 2x 4-16m 2y 4;
解:(1)原式=[(3a-2b)+(2a+3b)][(3a-2b)-(2a+3b)]
=(3a-2b+2a+3b)(3a-2b-2a-3b)
=(5a+b)(a-5b).
(2)原式=(x 2+9y 2)(x 2-9y 2)
=(x 2+9y 2)(x+3y )(x-3y ).
课堂练习
(3)原式=a 2(a 2-9b 2)
=a 2(a+3b)(a-3b).
(4)原式=m 2(x 4-16y 4)
=m 2(x 2+4y 2)(x 2-4y 2)
=m 2(x 2+4y 2)(x+2y )(x-2y )
课堂练习
7.计算下列各题:(1)1012-992; (2)53.52×4-46.52×4.
解:(1)原式=(101+99)(101-99)=400;
(2)原式=4×(53.52-46.52)
=4×(53.5+46.5)×(53.5-46.5)
=4×100×7=2800.
课堂总结
平方差公式分解因式
公式
a2-b2=(a+b)(a-b)
步骤
一提:公因式;
二套:公式;
三查:多项式的因式分解有没有分解到不能再分解为止.
板书设计
课题:4.3.1 公式法
一、a2-b2= (a+b)(a-b)
二、因式分解步骤
作业布置
【必做题】
教材100页习题4.4的1、2
【选做题】
教材第100页习题4.4的3题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
4.3.1公式法
北师版八年级下册
教学目标
1、探究能用平方差公式进行因式分解的多项式的特点;
2、会用平方差公式进行分解因式;
3、会综合运用提公因式法和平方差公式法分解因式.
新知导入
灰太狼开了个租地公司,一天他把一边长为a米的正方形土地租给慢羊羊村长种植.过了一年他对慢羊羊村长说:“我把这块地的一边减少5米,另一边增加5米,再继续租给你, 你也没吃亏,你看如何 ”
(a+5)(a-5)=
新知讲解
想一想:多项式x2-25, 9x2-y2能用提公因式法分解因式吗?如果不能,你有其他方法将它分解因式吗?
(1)观察多项式 x2-25 和 9x2-y2,它们有什么共同特征?
(2)尝试将它们分别写成两个因式的乘积.
多项式x2-25和9x2-y2都可以写成两个式子的平方差的形式:
x2-25=x2-52, 9x2-y2 =(3x)2-y2
把乘法公式(a+b)(a-b)=a2-b2反过来,就得到a2-b2=(a+b)(a-b),于是有:
x2-25=x2-52=(x+5)(x-5);
9x2-y2 =(3x)2-y2=(3x+y)(3x-y).
新知讲解
=(a+b)(a-b)
因式分解
两个数的平方差,等于这两个数的和与这两个数的差的乘积.
平方差公式:
你能用自己的语言描述这个公式吗?
新知讲解
1.多项式有两项;
2.这两项能写成平方差的形式,
即能写成:( )2-( )2的形式.
思考:一个多项式具备哪些特点才可以用平方差公式分解因式?
典例精析
例1 把下列各式因式分解:
(1)25-16x2; (2)9a2- b2.
解:(1) 25-16x2= 52-(4x)2=(5+4x)(5-4x);
(2)9a2-b2= (3a)2-(b)2=(3a+b)(3a-b)
归纳总结
利用平方差公式分解两项式的一般步骤:
1. 找出公式中的a、b;
2. 转化成a 2-b 2的形式;
3. 根据公式a 2-b 2=(a+b) (a-b) 写出结果.
典例精析
例2 把下列各式因式分解:
(1)9(m+n)2-(m-n)2; (2) 2x3-8x.
解:(1) 9(m+n)2-(m-n)2 =[3(m+n)]2-(m-n)2
= [3(m+n)+(m-n)] [3(m+n)-(m-n)]
= (3m+3n+m-n)(3m+3n-m+n)
=(4m+2n)(2m+4n)
=4(2m+n)(m+2n);
(2)2x3-8x=2x(x2-4) = 2x(x2-22) =2x (x+2)(x-2)
当多项式的各项含有公因式时,通常先提出这个公因式,然后再进一步因式分解
归纳总结
1.具有平方差形式的多项式才可运用平方差公式分解因式.
2.公式中的字母 可以是单项式,也可以是多项式,应视具体情形灵活运用.
3.公式中的a、b可以代表多项式,此时我们将多项式看成整体套用公式,改写平方形式时不要漏掉系数;
4.若多项式中有公因式,应先提取公因式,然后再进一步分解因式.
5.分解因式要彻底.要注意每一个因式的形式要最简,直到不能再分解为止.
课堂练习
1、把x 3-9x 分解因式,结果正确的是( )
A.x (x 2-9) B.x (x-3)2
C.x (x+3)2 D.x (x+3)(x-3)
D
2、一次课堂练习,小颖同学做了以下几道因式分解题,你认为她做得不够完整的是( )
A.x 3-x=x (x 2-1)
B.x 2y-y 3=y (x+y )(x-y )
C.-m 2+4n 2=(2n+m)(2n-m)
D.3p 2-27q 2=3( p+3q )( p-3q )
A
课堂练习
3、已知|x-y+2|+=0,
则x 2-y 2的值为________.
4、若x 2-9=(x-3)(x+a),则a=________.
5、已知a+b=3,a-b=5,则式子a 2-b 2的值是________.
-4
3
15
课堂练习
6、把下列各式分解因式:
(1)(3a-2b)2-(2a+3b)2; (2)x 4-81y 4;
(3)a 4-9a 2b 2; (4)m 2x 4-16m 2y 4;
解:(1)原式=[(3a-2b)+(2a+3b)][(3a-2b)-(2a+3b)]
=(3a-2b+2a+3b)(3a-2b-2a-3b)
=(5a+b)(a-5b).
(2)原式=(x 2+9y 2)(x 2-9y 2)
=(x 2+9y 2)(x+3y )(x-3y ).
课堂练习
(3)原式=a 2(a 2-9b 2)
=a 2(a+3b)(a-3b).
(4)原式=m 2(x 4-16y 4)
=m 2(x 2+4y 2)(x 2-4y 2)
=m 2(x 2+4y 2)(x+2y )(x-2y )
课堂练习
7.计算下列各题:(1)1012-992; (2)53.52×4-46.52×4.
解:(1)原式=(101+99)(101-99)=400;
(2)原式=4×(53.52-46.52)
=4×(53.5+46.5)×(53.5-46.5)
=4×100×7=2800.
课堂总结
平方差公式分解因式
公式
a2-b2=(a+b)(a-b)
步骤
一提:公因式;
二套:公式;
三查:多项式的因式分解有没有分解到不能再分解为止.
板书设计
课题:4.3.1 公式法
一、a2-b2= (a+b)(a-b)
二、因式分解步骤
作业布置
【必做题】
教材100页习题4.4的1、2
【选做题】
教材第100页习题4.4的3题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
