北师大版 七年级下册2.2 探索直线平行的条件 同步练习 (含解析)
文档属性
| 名称 | 北师大版 七年级下册2.2 探索直线平行的条件 同步练习 (含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 158.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-24 12:55:11 | ||
图片预览

文档简介
2.2 探索直线平行的条件 同步练习
一、单选题
1.已知三角形ABC,过AC的中点D作AB的平行线,根据语句作图正确的是( )
A. B. C. D.
2.如图,在平移三角尺画平行线的过程中,理由是( )
A.两直线平行,同位角相等
B.两直线平行,内错角相等
C.同位角相等,两直线平行
D.内错角相等,两直线平行
3.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.无法确定
4.下列命题中,不正确的是( )
A.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行
B.两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行
C.两条直线被第三条直线所截,那么这两条直线平行
D.如果两条直线都和第三条直线平行,那么这两条直线也互相平行
5.如图,可以推理得到AB∥CD的条件是( )
A.∠2=∠B B.∠1=∠A
C.∠3=∠B D.∠3=∠A
6.如图,下列能判定ABCD的条件有()个.
(1);(2);(3);(4).
A.1 B.2 C.3 D.4
7.如图,下列推理错误的是( )
A.∵∠1=∠3∴a∥b B.∵∠1=∠2∴a∥b
C.∵∠3=∠5∴c∥d D.∵∠2+∠4=180°∴c∥d
8.如图,其中内错角的对数是( )
A.5 B.2 C.3 D.4
9.下列说法正确的有( )
①两点之间的所有连线中,线段最短;②相等的角叫对顶角;③过一点有且只有一条直线与已知直线平行;④过一点有且只有一条直线与已知直线垂直;⑤两点之间的距离是两点间的线段;
A.1个 B.2个 C.3个 D.4个
10.如果a//b,b//c,那么a//c,这个推理的依据是 ( )
A.等量代换 B.经过直线外一点,有且只有一条直线与已知直线平行
C.平行线的定义 D.平行于同一直线的两直线平行
二、填空题
11.如图,与______互补,可以判定,与______互补,可以判定.
12.如图 ,已知直线AB∥CD,直线AB与EF相交于点P,那么直线EF也与直线CD相交,请在下面的推理过程中填空.
∵AB∥CD,AB.EF交于点P;
∴点P必在直线CD外.
假设直线EF和CD不相交,那么过点P就有两条直线.
AB和EF都与CD平行,这与____________公理矛盾.
∴直线EF也与直线CD相交.
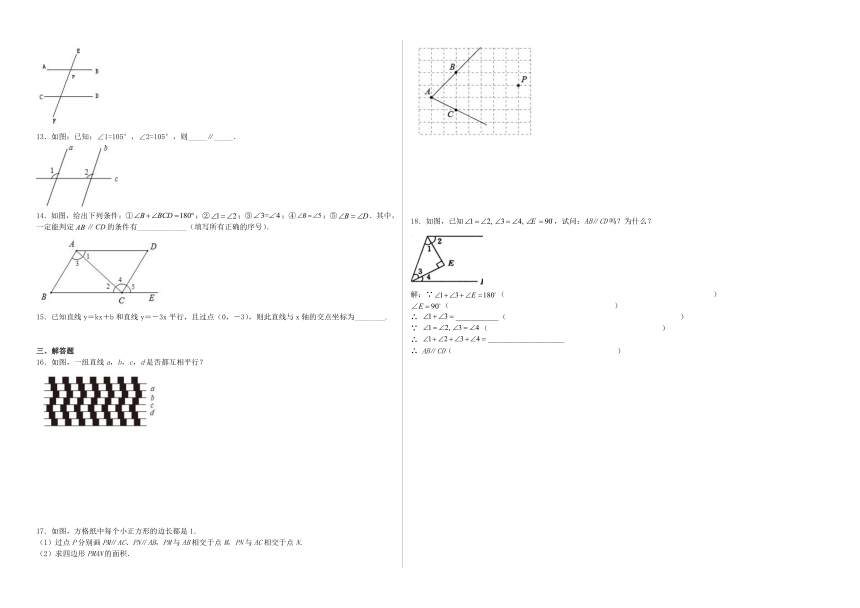
13.如图:已知:∠1=105°,∠2=105°,则_____∥_____.
14.如图,给出下列条件:①;②;③;④;⑤.其中,一定能判定∥的条件有_____________(填写所有正确的序号).
15.已知直线y=kx+b和直线y=-3x平行,且过点(0,-3),则此直线与x轴的交点坐标为________.
三、解答题
16.如图,一组直线a,b,c,d是否都互相平行?
17.如图,方格纸中每个小正方形的边长都是1.
(1)过点P分别画PM∥AC、PN∥AB,PM与AB相交于点M,PN与AC相交于点N.
(2)求四边形PMAN的面积.
18.如图,已知,试问:AB∥CD吗?为什么?
解:∵( )
( )
∴ ( )
∵ ( )
∴
∴ AB∥CD( )
第3页 共4页 ◎ 第4页 共4页
参考答案
1.B
【详解】解:过AC的中点D作AB的平行线,
正确的图形是选项B,
故选:B.
2.C
【详解】
∵∠DPF=∠BMF,
∴AB∥CD(同位角相等,两直线平行).
故选C.
3.A
【详解】由图形可知,同位角相等,两直线平行,
故选A.
4.C
【详解】A、B、D均为平行线的判定定理和性质定理,
C中的两条直线被第三条直线所截,如果内错角、同位角不相等,同旁内角不互补,那么这两条直线不平行,C错误.
故选C.
5.C
【详解】A. ∠2和∠B,不是由AB和CD组成的同位角、内错角、同旁内角,故本选项错误;
B. ∠1和∠A不是由直线AB和CD组成的同旁内角,故本选项错误;
C. ∵∠3=∠B,∴AB∥CD(同位角相等,两直线平行,故本选项正确;
D. ∠3和∠A不是由AB和CD组成的同位角、内错角、同旁内角,故本选项错误;
故选C.
6.C
【详解】解:当∠B+∠BCD=180°,ABCD,符合题意;
当∠1=∠2时,ADBC,不符合题意;
当∠3=∠4时,ABCD,符合题意;
当∠B=∠5时,ABCD,符合题意.
综上,符合题意的有3个,
故选:C.
7.A
详解:A. ∵∠1与∠3不具有特殊位置关系,∴不能推出a∥b ;
B. ∵∠1与∠2是一对内错角,∴由∠1=∠2能推出a∥b;
C. ∵∠3与∠5是一对同位角,∴由∠3=∠5能推出c∥d;
D. ∵∠2与∠4是一对同旁内角,∴由∠2+∠4=180°能推出c∥d.
故选A.
8.D
【详解】解:如图所示,是内错角的有:∠CAB与∠EBA;∠DAB与∠EBA;∠CAB与∠FBA;∠DAB与∠FBA,一共有4对.故选D.
9.A
【详解】①两点之间的所有连线中,线段最短,说法正确;
②对顶角相等,但相等的不一定是对顶角,也可能是内错角,同位角等,说法错误;
③过直线外一点有且只有一条直线与已知直线平行,说法错误;
④在同一平面内,过一点有且只有一条直线与已知直线垂直,说法错误;
⑤因为两点之间的距离是两点间线段的长度,而不是是两点间的线段,说法错误;
故选A.
10.D
【详解】如果a∥b,b∥c,那么a∥c,这个推理的依据是平行于同一直线的两直线平行.
故选D.
11.
【详解】∠A与∠D互补,可判定,∠B与∠A互补,可以判定.
故答案为∠D;∠A.
12.
【详解】∵AB∥CD,AB.EF交于点P;
∴点P必在直线CD外.
假设直线EF和CD不相交,那么过点P就有两条直线AB和EF都与CD平行,这与平行公理矛盾.
∴直线EF也与直线CD相交.
13.
【详解】解:∵∠1=105°,∠2=105°,∴∠1=∠2,∴a∥b.
故答案为a,b.
14.
【详解】① ∵,
∴∥(同旁内角互补,两直线平行),正确;
② ∵,
∴∥,错误;
③ ∵,
∴∥(内错角相等,两直线平行),正确;
④ ∵,
∴∥(同位角相等,两直线平行),正确;
⑤ 不能证明∥,错误,
故答案为:①③④.
15.
【详解】∵直线y=kx+b和直线y= 3x平行,
∴k= 3,
把(0, 3)代入y= 3x+b得b= 3,
∴直线解析式为y= 3x 3,
当y=0时, 3x 3=0,解得x= 1,
∴直线y= 3x 3与x轴的交点坐标为( 1,0).
故答案为( 1,0).
16.
【详解】解:直线a,b,c,d都互相平行,理由如下:
∵,
∴.
17.
【详解】解:(1)如图所示:点M,点N即为所求;
(2)四边形PMAN的面积为:5×7﹣×3×3﹣×2×4﹣×2×4﹣×3×3=18.
18.
【详解】∵∠1+∠3+∠E=180°(三角形的内角和等于180°)
∠E=90°(已知)
∴∠1+∠3=90°(等式的性质)
∵∠1=∠2,∠3=∠4(已知)
∴∠1+∠2+∠3+∠4=180°
∴AB∥CD(同旁内角互补,两直线平行)
答案第2页,共3页
一、单选题
1.已知三角形ABC,过AC的中点D作AB的平行线,根据语句作图正确的是( )
A. B. C. D.
2.如图,在平移三角尺画平行线的过程中,理由是( )
A.两直线平行,同位角相等
B.两直线平行,内错角相等
C.同位角相等,两直线平行
D.内错角相等,两直线平行
3.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.无法确定
4.下列命题中,不正确的是( )
A.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行
B.两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行
C.两条直线被第三条直线所截,那么这两条直线平行
D.如果两条直线都和第三条直线平行,那么这两条直线也互相平行
5.如图,可以推理得到AB∥CD的条件是( )
A.∠2=∠B B.∠1=∠A
C.∠3=∠B D.∠3=∠A
6.如图,下列能判定ABCD的条件有()个.
(1);(2);(3);(4).
A.1 B.2 C.3 D.4
7.如图,下列推理错误的是( )
A.∵∠1=∠3∴a∥b B.∵∠1=∠2∴a∥b
C.∵∠3=∠5∴c∥d D.∵∠2+∠4=180°∴c∥d
8.如图,其中内错角的对数是( )
A.5 B.2 C.3 D.4
9.下列说法正确的有( )
①两点之间的所有连线中,线段最短;②相等的角叫对顶角;③过一点有且只有一条直线与已知直线平行;④过一点有且只有一条直线与已知直线垂直;⑤两点之间的距离是两点间的线段;
A.1个 B.2个 C.3个 D.4个
10.如果a//b,b//c,那么a//c,这个推理的依据是 ( )
A.等量代换 B.经过直线外一点,有且只有一条直线与已知直线平行
C.平行线的定义 D.平行于同一直线的两直线平行
二、填空题
11.如图,与______互补,可以判定,与______互补,可以判定.
12.如图 ,已知直线AB∥CD,直线AB与EF相交于点P,那么直线EF也与直线CD相交,请在下面的推理过程中填空.
∵AB∥CD,AB.EF交于点P;
∴点P必在直线CD外.
假设直线EF和CD不相交,那么过点P就有两条直线.
AB和EF都与CD平行,这与____________公理矛盾.
∴直线EF也与直线CD相交.
13.如图:已知:∠1=105°,∠2=105°,则_____∥_____.
14.如图,给出下列条件:①;②;③;④;⑤.其中,一定能判定∥的条件有_____________(填写所有正确的序号).
15.已知直线y=kx+b和直线y=-3x平行,且过点(0,-3),则此直线与x轴的交点坐标为________.
三、解答题
16.如图,一组直线a,b,c,d是否都互相平行?
17.如图,方格纸中每个小正方形的边长都是1.
(1)过点P分别画PM∥AC、PN∥AB,PM与AB相交于点M,PN与AC相交于点N.
(2)求四边形PMAN的面积.
18.如图,已知,试问:AB∥CD吗?为什么?
解:∵( )
( )
∴ ( )
∵ ( )
∴
∴ AB∥CD( )
第3页 共4页 ◎ 第4页 共4页
参考答案
1.B
【详解】解:过AC的中点D作AB的平行线,
正确的图形是选项B,
故选:B.
2.C
【详解】
∵∠DPF=∠BMF,
∴AB∥CD(同位角相等,两直线平行).
故选C.
3.A
【详解】由图形可知,同位角相等,两直线平行,
故选A.
4.C
【详解】A、B、D均为平行线的判定定理和性质定理,
C中的两条直线被第三条直线所截,如果内错角、同位角不相等,同旁内角不互补,那么这两条直线不平行,C错误.
故选C.
5.C
【详解】A. ∠2和∠B,不是由AB和CD组成的同位角、内错角、同旁内角,故本选项错误;
B. ∠1和∠A不是由直线AB和CD组成的同旁内角,故本选项错误;
C. ∵∠3=∠B,∴AB∥CD(同位角相等,两直线平行,故本选项正确;
D. ∠3和∠A不是由AB和CD组成的同位角、内错角、同旁内角,故本选项错误;
故选C.
6.C
【详解】解:当∠B+∠BCD=180°,ABCD,符合题意;
当∠1=∠2时,ADBC,不符合题意;
当∠3=∠4时,ABCD,符合题意;
当∠B=∠5时,ABCD,符合题意.
综上,符合题意的有3个,
故选:C.
7.A
详解:A. ∵∠1与∠3不具有特殊位置关系,∴不能推出a∥b ;
B. ∵∠1与∠2是一对内错角,∴由∠1=∠2能推出a∥b;
C. ∵∠3与∠5是一对同位角,∴由∠3=∠5能推出c∥d;
D. ∵∠2与∠4是一对同旁内角,∴由∠2+∠4=180°能推出c∥d.
故选A.
8.D
【详解】解:如图所示,是内错角的有:∠CAB与∠EBA;∠DAB与∠EBA;∠CAB与∠FBA;∠DAB与∠FBA,一共有4对.故选D.
9.A
【详解】①两点之间的所有连线中,线段最短,说法正确;
②对顶角相等,但相等的不一定是对顶角,也可能是内错角,同位角等,说法错误;
③过直线外一点有且只有一条直线与已知直线平行,说法错误;
④在同一平面内,过一点有且只有一条直线与已知直线垂直,说法错误;
⑤因为两点之间的距离是两点间线段的长度,而不是是两点间的线段,说法错误;
故选A.
10.D
【详解】如果a∥b,b∥c,那么a∥c,这个推理的依据是平行于同一直线的两直线平行.
故选D.
11.
【详解】∠A与∠D互补,可判定,∠B与∠A互补,可以判定.
故答案为∠D;∠A.
12.
【详解】∵AB∥CD,AB.EF交于点P;
∴点P必在直线CD外.
假设直线EF和CD不相交,那么过点P就有两条直线AB和EF都与CD平行,这与平行公理矛盾.
∴直线EF也与直线CD相交.
13.
【详解】解:∵∠1=105°,∠2=105°,∴∠1=∠2,∴a∥b.
故答案为a,b.
14.
【详解】① ∵,
∴∥(同旁内角互补,两直线平行),正确;
② ∵,
∴∥,错误;
③ ∵,
∴∥(内错角相等,两直线平行),正确;
④ ∵,
∴∥(同位角相等,两直线平行),正确;
⑤ 不能证明∥,错误,
故答案为:①③④.
15.
【详解】∵直线y=kx+b和直线y= 3x平行,
∴k= 3,
把(0, 3)代入y= 3x+b得b= 3,
∴直线解析式为y= 3x 3,
当y=0时, 3x 3=0,解得x= 1,
∴直线y= 3x 3与x轴的交点坐标为( 1,0).
故答案为( 1,0).
16.
【详解】解:直线a,b,c,d都互相平行,理由如下:
∵,
∴.
17.
【详解】解:(1)如图所示:点M,点N即为所求;
(2)四边形PMAN的面积为:5×7﹣×3×3﹣×2×4﹣×2×4﹣×3×3=18.
18.
【详解】∵∠1+∠3+∠E=180°(三角形的内角和等于180°)
∠E=90°(已知)
∴∠1+∠3=90°(等式的性质)
∵∠1=∠2,∠3=∠4(已知)
∴∠1+∠2+∠3+∠4=180°
∴AB∥CD(同旁内角互补,两直线平行)
答案第2页,共3页
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
