人教版五年级数学上册 第二单元第2课时《用数对确定位置——在方格纸上》精品教学方案
文档属性
| 名称 | 人教版五年级数学上册 第二单元第2课时《用数对确定位置——在方格纸上》精品教学方案 |  | |
| 格式 | docx | ||
| 文件大小 | 390.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 15:12:05 | ||
图片预览


文档简介
第二单元 位置
第2课时 用数对确定位置——在方格纸上
教学内容分析:
本节课是在学生己经学会用数对确定物体位置的基础上教学的。创设在动物园示意图上确定各场馆位置的情境,通过学生熟悉的方格纸把用数对表示位置的实际问题转化成用数对表示平面上点的位置的数学问题,使学生明确如何在方格纸上用数对确定点的位置,进一步体会数形结合的思想,感悟数对与物体位置的一一对应关系,直观感受直角坐标系的思想。
教学目标:
1.结合方格纸用数对来确定物体的位置,能依据给定的数对在方格纸上确定位置。
2.让学生知道数对与方格纸上的点存在对应关系。
3.在确定位置过程中,增强学生解决实际问题能力,提高应用意识。
教学重点:
掌握在方格纸上用数对确定物体的位置。
教学难点:
正确描述物体所在的位置。
教学过程:
教学环节 教师活动 学生活动 设计意图
环节一 创设情境 【复习导入】 师:观察情境图,你知道第1列第3行坐着哪位同学吗? 师:怎样能简洁地表示座位图? 师:这个点表示什么? 那么,今天我们继续来学习在方格纸上用数对确定物体的位置。 生:周明。 生:用点表示每个同学,竖线与横线的交点就是每个同学的位置,座位图变成方格图了。 生:竖着看是列的开始,横着看是行的开始,可以用数对(0,0)来表示。 通过复习导入,巩固复习用数对表示物体位置的方法,并引导学生尝试将座位图抽象成方格图,对方格图有基本的认识。
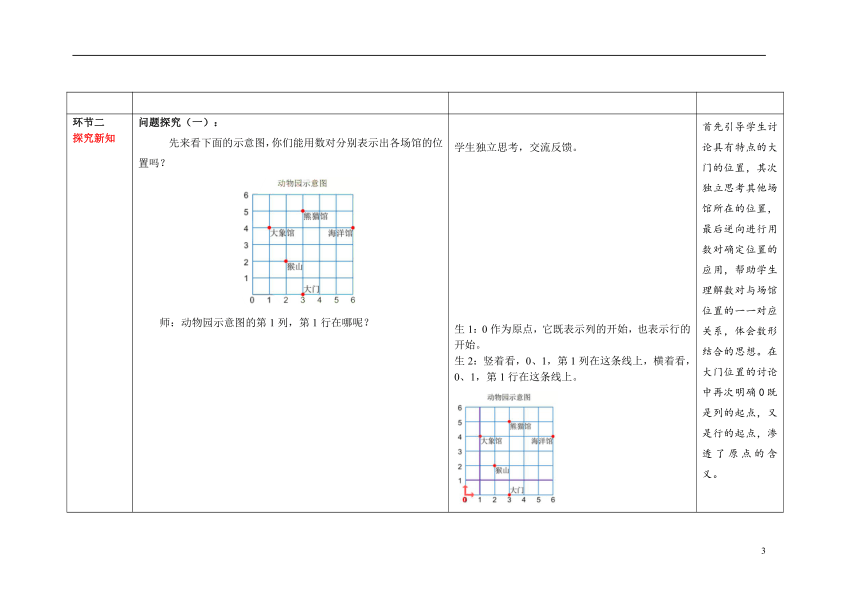
环节二 探究新知 问题探究(一): 先来看下面的示意图,你们能用数对分别表示出各场馆的位置吗? 师:动物园示意图的第1列,第1行在哪呢? 师:谁能用数对表示出大门的位置呢? 师:你还能用数对表示其他场馆所在的位置吗? 师:仔细观察方格,说说你有什么发现? 师:请你尝试着说一说,你发现了什么规律? 问题探究(二): 师:在图上标出下列场馆的位置。 飞禽馆(1,1) 猩猩馆(0,3) 狮虎山(4,3) 归纳总结: 师:怎样在方格纸上用数对确定物体的位置? 学生独立思考,交流反馈。 生1:0作为原点,它既表示列的开始,也表示行的开始。 生2:竖着看,0、1,第1列在这条线上,横着看,0、1,第1行在这条线上。 生:我用数对(3,0)表示大门的位置。 生1:大象馆(1,4) 生2:猴山(2,2) 生3:熊猫馆(3,5) 生4:海洋馆(6,4) 生1:熊猫馆和大门数对的第一个数都是3,表明它们在同一列上。 生2:大象馆和海洋馆数对的第二个数都是4,表明它们在同一行上。 生:(1)两数对中第一个数相同时,表明两个物体在同一列; (2)两数对中第二个数相同时,表明两个物体在同一行。 学生独立完成,同桌相互交流反馈。 生: 生: (1)在方格纸上,同样可以用数对表示物体的具体位置; (2)行和列的交点处,就是物体所在的位置。 首先引导学生讨论具有特点的大门的位置,其次独立思考其他场馆所在的位置,最后逆向进行用数对确定位置的应用,帮助学生理解数对与场馆位置的一一对应关系,体会数形结合的思想。在大门位置的讨论中再次明确0既是列的起点,又是行的起点,渗透了原点的含义。 引导学生观察熊猫馆、大门以及大象馆和海洋馆在图中的位置,并表示它们位置的数对。从中发现规律,两数对中第一个数相同时,表明两个物体在同一列;两数对中第二个数相同时,表明两个物体在同一行,培养学生分析问题能力和概括能力。 引导学生利用前面的学习经验,根据数对找出场馆的位置,培养学生知识迁移能力和独立解决问题的能力。
环节三 巩固新知 1.照样子写出下图中字母的位置。 A(5,8) B( ,) C( , ) D( , ) 2.描出下列各点并依次连成封闭图形,看看是什么图形。 A (5, 9) B (2, 1) C (9, 6) D (1, 6) E (8, 1) 3.先用数对表示线段端点的位置,再分别画出线段向右平移和向下平移3个单位后的图形,用数对表示平移后线段的位置。 学生独立完成,交流反馈。 生: B(2 ,5) C( 5,2 ) D(8 ,5) 学生独立完成。 生: 生: A(5,9),B(4,7),向右平移3个单位后对应的数对分别是(8,9),B(7,7)。 A(5,9),B(4,7),向下平移3个单位后对应的数对分别是(5,6),B(4,4)。 第1、2题既有根据点(位置),写出表示它们位置的数对,又有根据点的数对,寻找相应位置的练习。通过练习,让学生初步体会数形结合的思想,建立图形和数之间的联系。体会图形特点和数对特点之间的联系。 结合线段运动让学生寻找对应的结果,用数对表示图形运动后的位置。
环节四 课堂小结 你有什么收获? 生: 1.知道了两数对中第一个数相同时,表明两个物体在同一列;第二个数相同时,表明两个物体在同一行。 2. 用数对可以表示平面上物体的位置。行和列的交点处,就是物体所在的位置。 鼓励学生畅谈自己的收获和体会,小结课堂,提升总结、表达能力。
环节五 拓展延伸 数对的由来 同学们认识了数对,可是你们知道数对的由来吗?笛卡尔是著名的法国数学家。有一天,他正在反复思考一个问题:怎样才能将“点”和“数”联系起来呢?突然,他看见屋角上的一只蜘蛛在上边左右拉丝。于是在蜘蛛的启示下,笛卡尔用一对有顺序的数表示平面上的一个点,并发明数对。 在我们的生活中蕴藏着许多的奥秘,同学们要学会用数学的眼光观察生活、了解生活,善于发现,勤于积累,将来你也能成为一名数学家。 增加学生的知识面和见闻。
环节六 布置作业 教材P21第3题 教材P23第7、8题
1
第2课时 用数对确定位置——在方格纸上
教学内容分析:
本节课是在学生己经学会用数对确定物体位置的基础上教学的。创设在动物园示意图上确定各场馆位置的情境,通过学生熟悉的方格纸把用数对表示位置的实际问题转化成用数对表示平面上点的位置的数学问题,使学生明确如何在方格纸上用数对确定点的位置,进一步体会数形结合的思想,感悟数对与物体位置的一一对应关系,直观感受直角坐标系的思想。
教学目标:
1.结合方格纸用数对来确定物体的位置,能依据给定的数对在方格纸上确定位置。
2.让学生知道数对与方格纸上的点存在对应关系。
3.在确定位置过程中,增强学生解决实际问题能力,提高应用意识。
教学重点:
掌握在方格纸上用数对确定物体的位置。
教学难点:
正确描述物体所在的位置。
教学过程:
教学环节 教师活动 学生活动 设计意图
环节一 创设情境 【复习导入】 师:观察情境图,你知道第1列第3行坐着哪位同学吗? 师:怎样能简洁地表示座位图? 师:这个点表示什么? 那么,今天我们继续来学习在方格纸上用数对确定物体的位置。 生:周明。 生:用点表示每个同学,竖线与横线的交点就是每个同学的位置,座位图变成方格图了。 生:竖着看是列的开始,横着看是行的开始,可以用数对(0,0)来表示。 通过复习导入,巩固复习用数对表示物体位置的方法,并引导学生尝试将座位图抽象成方格图,对方格图有基本的认识。
环节二 探究新知 问题探究(一): 先来看下面的示意图,你们能用数对分别表示出各场馆的位置吗? 师:动物园示意图的第1列,第1行在哪呢? 师:谁能用数对表示出大门的位置呢? 师:你还能用数对表示其他场馆所在的位置吗? 师:仔细观察方格,说说你有什么发现? 师:请你尝试着说一说,你发现了什么规律? 问题探究(二): 师:在图上标出下列场馆的位置。 飞禽馆(1,1) 猩猩馆(0,3) 狮虎山(4,3) 归纳总结: 师:怎样在方格纸上用数对确定物体的位置? 学生独立思考,交流反馈。 生1:0作为原点,它既表示列的开始,也表示行的开始。 生2:竖着看,0、1,第1列在这条线上,横着看,0、1,第1行在这条线上。 生:我用数对(3,0)表示大门的位置。 生1:大象馆(1,4) 生2:猴山(2,2) 生3:熊猫馆(3,5) 生4:海洋馆(6,4) 生1:熊猫馆和大门数对的第一个数都是3,表明它们在同一列上。 生2:大象馆和海洋馆数对的第二个数都是4,表明它们在同一行上。 生:(1)两数对中第一个数相同时,表明两个物体在同一列; (2)两数对中第二个数相同时,表明两个物体在同一行。 学生独立完成,同桌相互交流反馈。 生: 生: (1)在方格纸上,同样可以用数对表示物体的具体位置; (2)行和列的交点处,就是物体所在的位置。 首先引导学生讨论具有特点的大门的位置,其次独立思考其他场馆所在的位置,最后逆向进行用数对确定位置的应用,帮助学生理解数对与场馆位置的一一对应关系,体会数形结合的思想。在大门位置的讨论中再次明确0既是列的起点,又是行的起点,渗透了原点的含义。 引导学生观察熊猫馆、大门以及大象馆和海洋馆在图中的位置,并表示它们位置的数对。从中发现规律,两数对中第一个数相同时,表明两个物体在同一列;两数对中第二个数相同时,表明两个物体在同一行,培养学生分析问题能力和概括能力。 引导学生利用前面的学习经验,根据数对找出场馆的位置,培养学生知识迁移能力和独立解决问题的能力。
环节三 巩固新知 1.照样子写出下图中字母的位置。 A(5,8) B( ,) C( , ) D( , ) 2.描出下列各点并依次连成封闭图形,看看是什么图形。 A (5, 9) B (2, 1) C (9, 6) D (1, 6) E (8, 1) 3.先用数对表示线段端点的位置,再分别画出线段向右平移和向下平移3个单位后的图形,用数对表示平移后线段的位置。 学生独立完成,交流反馈。 生: B(2 ,5) C( 5,2 ) D(8 ,5) 学生独立完成。 生: 生: A(5,9),B(4,7),向右平移3个单位后对应的数对分别是(8,9),B(7,7)。 A(5,9),B(4,7),向下平移3个单位后对应的数对分别是(5,6),B(4,4)。 第1、2题既有根据点(位置),写出表示它们位置的数对,又有根据点的数对,寻找相应位置的练习。通过练习,让学生初步体会数形结合的思想,建立图形和数之间的联系。体会图形特点和数对特点之间的联系。 结合线段运动让学生寻找对应的结果,用数对表示图形运动后的位置。
环节四 课堂小结 你有什么收获? 生: 1.知道了两数对中第一个数相同时,表明两个物体在同一列;第二个数相同时,表明两个物体在同一行。 2. 用数对可以表示平面上物体的位置。行和列的交点处,就是物体所在的位置。 鼓励学生畅谈自己的收获和体会,小结课堂,提升总结、表达能力。
环节五 拓展延伸 数对的由来 同学们认识了数对,可是你们知道数对的由来吗?笛卡尔是著名的法国数学家。有一天,他正在反复思考一个问题:怎样才能将“点”和“数”联系起来呢?突然,他看见屋角上的一只蜘蛛在上边左右拉丝。于是在蜘蛛的启示下,笛卡尔用一对有顺序的数表示平面上的一个点,并发明数对。 在我们的生活中蕴藏着许多的奥秘,同学们要学会用数学的眼光观察生活、了解生活,善于发现,勤于积累,将来你也能成为一名数学家。 增加学生的知识面和见闻。
环节六 布置作业 教材P21第3题 教材P23第7、8题
1
