人教版五年级数学上册 第六单元第1课时平行四边形的面积精品教学方案
文档属性
| 名称 | 人教版五年级数学上册 第六单元第1课时平行四边形的面积精品教学方案 | 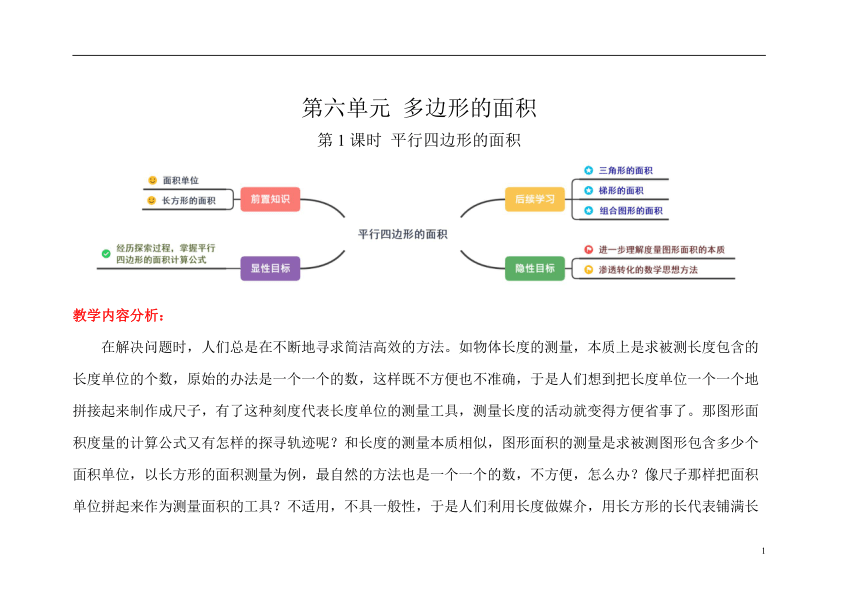 | |
| 格式 | docx | ||
| 文件大小 | 524.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 15:12:16 | ||
图片预览




文档简介
第六单元 多边形的面积
第1课时 平行四边形的面积
教学内容分析:
在解决问题时,人们总是在不断地寻求简洁高效的方法。如物体长度的测量,本质上是求被测长度包含的长度单位的个数,原始的办法是一个一个的数,这样既不方便也不准确,于是人们想到把长度单位一个一个地拼接起来制作成尺子,有了这种刻度代表长度单位的测量工具,测量长度的活动就变得方便省事了。那图形面积度量的计算公式又有怎样的探寻轨迹呢?和长度的测量本质相似,图形面积的测量是求被测图形包含多少个面积单位,以长方形的面积测量为例,最自然的方法也是一个一个的数,不方便,怎么办?像尺子那样把面积单位拼起来作为测量面积的工具?不适用,不具一般性,于是人们利用长度做媒介,用长方形的长代表铺满长方形一行的面积单位的个数,用宽衡量有这样的几行,这样用“长×宽”就能计算出长方形包含的面积单位的个数,由此将长方形面积的度量转化为了长度的计算。在此基础上,其他基本图形的面积就可以通过等积变形,实现图形间的转化来进行度量了。平行四边形面积公式的推导思路就是如此,用割补的方法沿高剪开再拼接成长方形。教学过程不应只局限于这种方法结果,应让学生经历探寻过程经历从测量本质出发,数方格测面积——凑整方格、优化凑法——转化为长方形的过程,由此了解方法的前因后果,知其然还知其所以然,领悟学习数学的思想方法。这也是不同版本的教材基本都照此思路编排的原因,但有的教材在引出方格数面积之前,预设了学生求平行四边形的一种思路:邻边相乘,这是由学生的前置经验和认知特点,从长方形的面积计算公式:长×宽,迁移出的平行四边形的面积计算公式:邻边×邻边。但有可能也有学生知道平行四边形的面积计算公式:底×高。教学正好可以抓住学生两种不同的思路,提出用方格数一数进行判断,以此引出方格,让学生感受面积测量的本质。
教学目标:
1.通过操作、观察、比较等活动,自主探索平行四边形面积计算公式,经历等积变形的过程,渗透转化的数学思想方法。
2.能正确地应用公式计算平行四边形的面积。
3.培养学生合作意识和探索精神。
教学重点:
探索并掌握平行四边形面积计算公式。
教学难点:
理解平行四边形面积计算公式的推导过程,体会转化的思想。
教学过程:
教学环节 教师活动 学生活动 设计意图
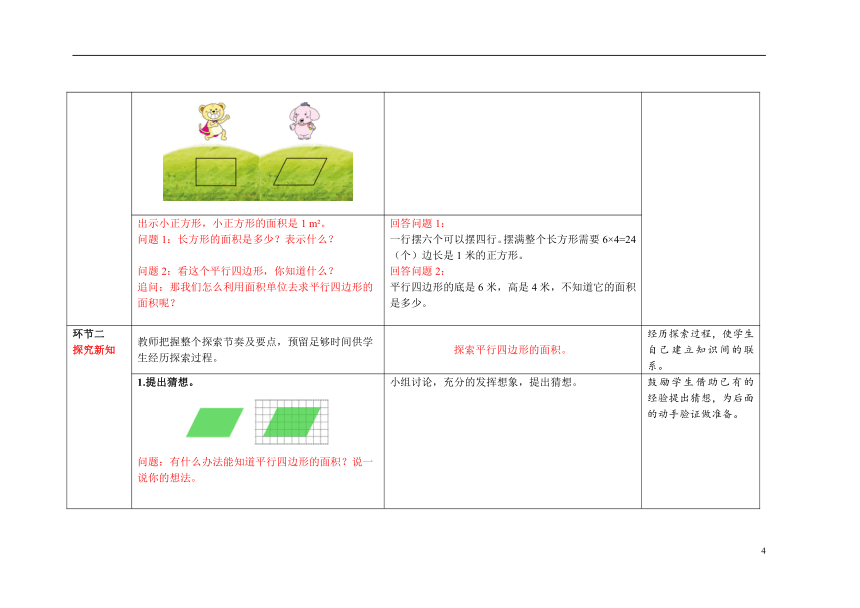
环节一 创设情境 两个动物在森林里分别画了一块草地比较大小,一个画了一块长方形草地,一个画的是一块平行四边形的草地,你能给他们评比一下谁的草地面积大吗? 仔细听老师的问题,思考要想评比谁的面积大,需要知道什么,哪些是已知的,哪些是未知的。 一是回顾长方形的面积、面积单位的意义;二是为后面的探索提供思路,学生首先想到是怎样比较长方形和平行四边形的面积,浅意识的去转化。
出示小正方形,小正方形的面积是1 m 。 问题1:长方形的面积是多少?表示什么? 问题2:看这个平行四边形,你知道什么? 追问:那我们怎么利用面积单位去求平行四边形的面积呢? 回答问题1: 一行摆六个可以摆四行。摆满整个长方形需要6×4=24(个)边长是1米的正方形。 回答问题2: 平行四边形的底是6米,高是4米,不知道它的面积是多少。
环节二 探究新知 教师把握整个探索节奏及要点,预留足够时间供学生经历探索过程。 探索平行四边形的面积。 经历探索过程,使学生自己建立知识间的联系。
1.提出猜想。 问题:有什么办法能知道平行四边形的面积?说一说你的想法。 教师将学生的想法进行归类。 小组讨论,充分的发挥想象,提出猜想。 鼓励学生借助已有的经验提出猜想,为后面的动手验证做准备。
2.动手验证。 在学生操作过程中,教师应预留充分的时间供学生寻找方法,进行尝试。 借助正方形网格、涂色笔、剪刀动手操作。 (1)选择合适的材料,进行验证。 (2)反馈交流,计算平行四边形的面积到底是多少。 方法一: 利用数格子的方式进行估计。 学生可能会有不同的估计方式,不满一格的不算(或不满一格的都按半格算或不满一格的按一格算)。 方法二: 利用整合小格子的方式通过面积单位的意义进行计算。 方法三: 利用画图或剪刀将平行四边形转化成长方形。 通过动手操作去验证,将图形进行等积变形,学生可能经历由估计开始,也可能用涂色的方式转化成整格的,也可能学生很快的将平行四边形转化成长方形,该环节注重学生是否主动参与,是否能说出自己这么做的道理。
3.深入辨析。 问题:是不是所有的平行四边形的面积都是这样计算呢? 鼓励学生不仅左右平移转化成长方形,还可以上下平移得到长方形。另外,平行四边形本身也可以转化成等底等高的平行四边形,不管怎样变化,都可以保证面积不变,形状变化。 活动:在方格纸上任意画一个平行四边形。(拼的次数越少,水平越高) 再次经历探索过程,再次经历基本方法,交流方法,体会等积变形。发现只要沿着平行四边形的高来剪,出现直角,这样平行四边形都是可以转化成长方形的。 从上面教师给出的一个平行四边形过渡到学生自己画的不一样的平行四边形,再次经历探索过程,再次经历基本方法,体会沿着高来分割,出现直角,就能将平行四边形转化成长方形。
4.公式推导。 通过转化,我们知道了转化后长方形的面积与原来平行四边形的面积相等,长方形的长与原来平行四边形的底相等,长方形的宽与原来平行四边形的高相等。我们知道长方形的面积等于长乘宽,所以平行四边形的面积等于底乘高。 沟通平行四边形和转化后的长方形的对应关系。
5.应用公式解决问题。 同学们已经推导出了平行四边形的面积计算公式,现在你能解决情境中的问题吗? 预设: 长方形的长是6 m,宽是4 m,它的面积是24 m 。 平行四边形的底是6 m,对应的高是4 m,它的面积是24 m 。 它们的面积是一样的。 学生推导出平行四边形的面积计算公式后,首先返回去解决情境中提出的问题,明确要想计算平行四边形的面积,需要知道哪些条件。
6.提出疑问。 出示平行四边形框架。 问题1:平行四边形的框架怎样变成长方形呢? 追问:什么变了?什么没有变? 问题2:两个图形的面积一样吗? 预设:平行四边形拉成长方形,平行四边形的四条边没有变,平行四边形的高变了。 预设:在拉动平行四边形框架的过程中,底不变,高逐渐变大,所以面积越来越大。 学生已经对平行四边形的面积有了一定的认识,此时抛出一个问题,激发学生去思考、去说理。
7.回顾深化。 通过探究我们推导出了平行四边形的面积计算公式。 如果用a表示底,h表示高,S表示面积,平行四边形的面积公式还可以写成:S=ah。 平行四边形的面积和底、高有关,只要底和高的数值不变,平行四边形的形状可以变化,请你判断一下这些平行四边形的面积都相等吗?(它们的底和高都相等) 回顾探索过程,加深对平行四边形面积公式的理解。 预设:等底等高的平行四边形,它们的面积都是相等的。 回顾推导过程,梳理小结。
环节三 巩固新知 1.如图,平行四边形的面积,正确算式是( ) A.4.8×6 B.10×8 C.6×8 2.如图,两条平行线之间画了一个长方形和一个平行四边形。长方形的长是8厘米,宽是6厘米,则平行四边形的面积是 cm 。 3.如图,平行四边形的周长是54 cm,平行四边形的面积是多少平方厘米? C 48 (54-12×2)÷2×10 =30÷2×10 =150(cm ) 答:这个平行四边形的面积是150 cm 。 测评学生对平行四边形面积计算公式的掌握情况。
环节四 课堂小结 你有什么收获? 回顾本节课自己的体会和收获。 鼓励学生畅谈自己的收获和体会,有哪些认知上的冲突,遇到问题是如何解决的。
环节五 布置作业 教材P90第6题~第9题。
1
第1课时 平行四边形的面积
教学内容分析:
在解决问题时,人们总是在不断地寻求简洁高效的方法。如物体长度的测量,本质上是求被测长度包含的长度单位的个数,原始的办法是一个一个的数,这样既不方便也不准确,于是人们想到把长度单位一个一个地拼接起来制作成尺子,有了这种刻度代表长度单位的测量工具,测量长度的活动就变得方便省事了。那图形面积度量的计算公式又有怎样的探寻轨迹呢?和长度的测量本质相似,图形面积的测量是求被测图形包含多少个面积单位,以长方形的面积测量为例,最自然的方法也是一个一个的数,不方便,怎么办?像尺子那样把面积单位拼起来作为测量面积的工具?不适用,不具一般性,于是人们利用长度做媒介,用长方形的长代表铺满长方形一行的面积单位的个数,用宽衡量有这样的几行,这样用“长×宽”就能计算出长方形包含的面积单位的个数,由此将长方形面积的度量转化为了长度的计算。在此基础上,其他基本图形的面积就可以通过等积变形,实现图形间的转化来进行度量了。平行四边形面积公式的推导思路就是如此,用割补的方法沿高剪开再拼接成长方形。教学过程不应只局限于这种方法结果,应让学生经历探寻过程经历从测量本质出发,数方格测面积——凑整方格、优化凑法——转化为长方形的过程,由此了解方法的前因后果,知其然还知其所以然,领悟学习数学的思想方法。这也是不同版本的教材基本都照此思路编排的原因,但有的教材在引出方格数面积之前,预设了学生求平行四边形的一种思路:邻边相乘,这是由学生的前置经验和认知特点,从长方形的面积计算公式:长×宽,迁移出的平行四边形的面积计算公式:邻边×邻边。但有可能也有学生知道平行四边形的面积计算公式:底×高。教学正好可以抓住学生两种不同的思路,提出用方格数一数进行判断,以此引出方格,让学生感受面积测量的本质。
教学目标:
1.通过操作、观察、比较等活动,自主探索平行四边形面积计算公式,经历等积变形的过程,渗透转化的数学思想方法。
2.能正确地应用公式计算平行四边形的面积。
3.培养学生合作意识和探索精神。
教学重点:
探索并掌握平行四边形面积计算公式。
教学难点:
理解平行四边形面积计算公式的推导过程,体会转化的思想。
教学过程:
教学环节 教师活动 学生活动 设计意图
环节一 创设情境 两个动物在森林里分别画了一块草地比较大小,一个画了一块长方形草地,一个画的是一块平行四边形的草地,你能给他们评比一下谁的草地面积大吗? 仔细听老师的问题,思考要想评比谁的面积大,需要知道什么,哪些是已知的,哪些是未知的。 一是回顾长方形的面积、面积单位的意义;二是为后面的探索提供思路,学生首先想到是怎样比较长方形和平行四边形的面积,浅意识的去转化。
出示小正方形,小正方形的面积是1 m 。 问题1:长方形的面积是多少?表示什么? 问题2:看这个平行四边形,你知道什么? 追问:那我们怎么利用面积单位去求平行四边形的面积呢? 回答问题1: 一行摆六个可以摆四行。摆满整个长方形需要6×4=24(个)边长是1米的正方形。 回答问题2: 平行四边形的底是6米,高是4米,不知道它的面积是多少。
环节二 探究新知 教师把握整个探索节奏及要点,预留足够时间供学生经历探索过程。 探索平行四边形的面积。 经历探索过程,使学生自己建立知识间的联系。
1.提出猜想。 问题:有什么办法能知道平行四边形的面积?说一说你的想法。 教师将学生的想法进行归类。 小组讨论,充分的发挥想象,提出猜想。 鼓励学生借助已有的经验提出猜想,为后面的动手验证做准备。
2.动手验证。 在学生操作过程中,教师应预留充分的时间供学生寻找方法,进行尝试。 借助正方形网格、涂色笔、剪刀动手操作。 (1)选择合适的材料,进行验证。 (2)反馈交流,计算平行四边形的面积到底是多少。 方法一: 利用数格子的方式进行估计。 学生可能会有不同的估计方式,不满一格的不算(或不满一格的都按半格算或不满一格的按一格算)。 方法二: 利用整合小格子的方式通过面积单位的意义进行计算。 方法三: 利用画图或剪刀将平行四边形转化成长方形。 通过动手操作去验证,将图形进行等积变形,学生可能经历由估计开始,也可能用涂色的方式转化成整格的,也可能学生很快的将平行四边形转化成长方形,该环节注重学生是否主动参与,是否能说出自己这么做的道理。
3.深入辨析。 问题:是不是所有的平行四边形的面积都是这样计算呢? 鼓励学生不仅左右平移转化成长方形,还可以上下平移得到长方形。另外,平行四边形本身也可以转化成等底等高的平行四边形,不管怎样变化,都可以保证面积不变,形状变化。 活动:在方格纸上任意画一个平行四边形。(拼的次数越少,水平越高) 再次经历探索过程,再次经历基本方法,交流方法,体会等积变形。发现只要沿着平行四边形的高来剪,出现直角,这样平行四边形都是可以转化成长方形的。 从上面教师给出的一个平行四边形过渡到学生自己画的不一样的平行四边形,再次经历探索过程,再次经历基本方法,体会沿着高来分割,出现直角,就能将平行四边形转化成长方形。
4.公式推导。 通过转化,我们知道了转化后长方形的面积与原来平行四边形的面积相等,长方形的长与原来平行四边形的底相等,长方形的宽与原来平行四边形的高相等。我们知道长方形的面积等于长乘宽,所以平行四边形的面积等于底乘高。 沟通平行四边形和转化后的长方形的对应关系。
5.应用公式解决问题。 同学们已经推导出了平行四边形的面积计算公式,现在你能解决情境中的问题吗? 预设: 长方形的长是6 m,宽是4 m,它的面积是24 m 。 平行四边形的底是6 m,对应的高是4 m,它的面积是24 m 。 它们的面积是一样的。 学生推导出平行四边形的面积计算公式后,首先返回去解决情境中提出的问题,明确要想计算平行四边形的面积,需要知道哪些条件。
6.提出疑问。 出示平行四边形框架。 问题1:平行四边形的框架怎样变成长方形呢? 追问:什么变了?什么没有变? 问题2:两个图形的面积一样吗? 预设:平行四边形拉成长方形,平行四边形的四条边没有变,平行四边形的高变了。 预设:在拉动平行四边形框架的过程中,底不变,高逐渐变大,所以面积越来越大。 学生已经对平行四边形的面积有了一定的认识,此时抛出一个问题,激发学生去思考、去说理。
7.回顾深化。 通过探究我们推导出了平行四边形的面积计算公式。 如果用a表示底,h表示高,S表示面积,平行四边形的面积公式还可以写成:S=ah。 平行四边形的面积和底、高有关,只要底和高的数值不变,平行四边形的形状可以变化,请你判断一下这些平行四边形的面积都相等吗?(它们的底和高都相等) 回顾探索过程,加深对平行四边形面积公式的理解。 预设:等底等高的平行四边形,它们的面积都是相等的。 回顾推导过程,梳理小结。
环节三 巩固新知 1.如图,平行四边形的面积,正确算式是( ) A.4.8×6 B.10×8 C.6×8 2.如图,两条平行线之间画了一个长方形和一个平行四边形。长方形的长是8厘米,宽是6厘米,则平行四边形的面积是 cm 。 3.如图,平行四边形的周长是54 cm,平行四边形的面积是多少平方厘米? C 48 (54-12×2)÷2×10 =30÷2×10 =150(cm ) 答:这个平行四边形的面积是150 cm 。 测评学生对平行四边形面积计算公式的掌握情况。
环节四 课堂小结 你有什么收获? 回顾本节课自己的体会和收获。 鼓励学生畅谈自己的收获和体会,有哪些认知上的冲突,遇到问题是如何解决的。
环节五 布置作业 教材P90第6题~第9题。
1
